
 |
A 2004. decemberi B-jelĹą matematika feladatok megoldĂĄsa |
A kĂśzĂśltek csak megoldĂĄsvĂĄzlatok, esetleg csak vĂŠgeredmĂŠnyek. A maximĂĄlis pontszĂĄm elĂŠrĂŠsĂŠhez ĂĄltalĂĄban ennĂŠl rĂŠszletesebb megoldĂĄs szĂźksĂŠges. A rĂŠszletes megoldĂĄsokat a bekĂźldĂśtt dolgozatok alapjĂĄn a KĂśMaL-ban folyamatosan kĂśzĂśljĂźk.
B.3772. HĂĄny olyan (n;k) szĂĄmpĂĄr van, amelyre n>k, tovĂĄbbĂĄ az n ĂŠs k oldalĂş szabĂĄlyos sokszĂśgek belsĹ szĂśgĂŠnek az eltĂŠrĂŠse 1o?
(4 pont)
MegoldĂĄs: Mivel a belsĹ szĂśgek eltĂŠrĂŠse megegyezik a kĂźlsĹ szĂśgek eltĂŠrĂŠsĂŠvel, a mĂĄsodik feltĂŠtel ekvivalens a
\(\displaystyle {360\over k}-{360\over n}=1\)
feltĂŠtellel, amit ekvivalens ĂĄtalakĂtĂĄsokkal
360n-360k=nk, (360-k)(360+n)=3602
alakra hozhatunk. A k ĂŠs n szĂĄmokra tovĂĄbbi feltĂŠteleink: 3\(\displaystyle \le\)k\(\displaystyle \le\)n. Mivel (360-k)(360+k)<3602, a (360-k)(360+n)=3602 feltĂŠtel teljesĂźlĂŠse esetĂŠn k<n automatikusan teljesĂźlni fog. Minden 3602=a.b alakĂş elĹĂĄllĂtĂĄs, ahol a,b pozitĂv egĂŠsz szĂĄmok ĂŠs a\(\displaystyle \le\)357, megfelel tehĂĄt egy alkalmas (n,k) szĂĄmpĂĄrnak, ahol k=360-a ĂŠs n=b-360, ĂŠs az is vilĂĄgos, hogy minden megfelelĹ szĂĄmpĂĄrt megkapunk ilyen mĂłdon. Mivel pedig sem 358, sem 359 nem osztĂłja a 3602 szĂĄmnak, az a,b pozitĂv egĂŠszekre adott feltĂŠtel ekvivalens az a<b feltĂŠtellel.
A 3602=26.34.52 prĂmtĂŠnyezĹs felbontĂĄs alapjĂĄn lĂĄthatĂł hogy 3602 pozitĂv osztĂłinak szĂĄma (6+1)(4+1)(2+1)=105. EzĂŠrt a 3602 szĂĄmot, nagysĂĄgrendi megkĂśtĂŠsek nĂŠlkĂźl, ĂŠppen 105 fĂŠlekĂŠppen lehet a.b alakban felĂrni, ahol a,b pozitĂv egĂŠsz szĂĄmok. EbbĹl a 360.360 elĹĂĄllĂtĂĄs nem lesz megfelelĹ, a tĂśbbi 104 elĹĂĄllĂtĂĄsnak pedig pontosan felĂŠben fog teljesĂźlni az a<b feltĂŠtel. A szĂłban forgĂł (n,k) szĂĄmpĂĄrok szĂĄma tehĂĄt 52.
B.3773. OszthatĂł-e
202004+162004-32004-1
323-mal?
(3 pont)
MegoldĂĄs: Mivel 323=17.19, vizsgĂĄljuk meg azt, hogy az adott szĂĄm oszthatĂł-e 17-tel, illetve 19-cel. Ismeretes, hogy ha a ĂŠs b kĂźlĂśnbĂśzĹ egĂŠsz szĂĄmok, n pedig termĂŠsztes szĂĄm, akkor an-bn oszthatĂł (a-b)-vel. EbbĹl az is kĂśvetkezik, hogy ha a2 ĂŠs b2 is kĂźlĂśnbĂśzĹ, tovĂĄbbĂĄ n pĂĄros, akkor an-bn oszthatĂł (a2-b2)-tel, kĂśvetkezĂŠskĂŠppen (a+b)-vel is.
Ezt alkalmazva lĂĄthatĂł, hogy
17 | 202004-32004, 17 | 162004-12004, 19 | 202004-12004, 19 | 162004-32004.
Vagyis a szĂłban forgĂł szĂĄm oszthatĂł mind 17-tel, mind 19-cel. Mivel 17 ĂŠs 19 relatĂv prĂmek, a szĂĄm a szorzatukkal, 323-mal is oszthatĂł.
B.3774. Az egyenlĹ szĂĄrĂş derĂŠkszĂśgĹą ABC hĂĄromszĂśg AB ĂĄtfogĂłjĂĄn adottak a K ĂŠs az M pontok. K az A ĂŠs az M kĂśzĂśtt van, tovĂĄbbĂĄ KCM\(\displaystyle \angle\)=45o. BizonyĂtsuk be, hogy AK2+MB2=KM2.
(3 pont)
MegoldĂĄs: Legyen az A illetve B pontok tĂźkĂśrkĂŠpe a CK illetve CM egyenesre rendre A' ĂŠs B'. Mivel az ACK ĂŠs BCM szĂśgek Ăśsszege 45o, az ACA' ĂŠs BCB' szĂśgek Ăśsszege 90o lesz. Mivel pedig CA'=CA=CB=CB', az A' ĂŠs B' pontok egybeesnek. Mivel a CKA=CKA' ĂŠs CMB=CMB' szĂśgek a KMC hĂĄromszĂśg egy-egy szĂśgĂŠt egĂŠszĂtik ki 180o-ra, ĂśsszegĂźk ĂŠppen 180o-kal lesz nagyobb a KMC hĂĄromszĂśg harmadik, 45o-os szĂśgĂŠnĂŠl. A CKA'M nĂŠgyszĂśg A'-nĂŠl lĂŠvĹ szĂśge tehĂĄt derĂŠkszĂśg, vagyis a Pithagorasz-tĂŠtel szerint
AK2+MB2=A'K2+A'M2=KM2.
B.3775. Oldjuk meg az
y3=x3+8x2-6x+8
egyenletet a nemnegatĂv egĂŠszek kĂśrĂŠben.
(4 pont)
MegoldĂĄs: Ha x>9, akkor 2x2>18x, tehĂĄt
(x+2)3=x3+6x2+12x+8<x3+8x2-6x+8.
MĂĄsrĂŠszt tetszĹleges nemnegatĂv x szĂĄm esetĂŠn
x3+8x2-6x+8<x3+9x2+27x+27=(x+3)3.
EzĂŠrt x>9 esetĂŠn az x3+8x2-6x+8 szĂĄm kĂŠt egymĂĄst kĂśvetĹ pozitĂv egĂŠsz szĂĄm harmadik hatvĂĄnya kĂśzĂŠ esik, Ăgy nem lehet kĂśbszĂĄm. A 9-nĂŠl nem nagyobb nemnegatĂv egĂŠsz szĂĄmokat megvizsgĂĄlva pedig azt tapasztaljuk, hogy az x3+8x2-6x+8 szĂĄm csak x=0 ĂŠs x=9 esetĂŠn lesz kĂśbszĂĄm. Az egyenlĹsĂŠgnek tehĂĄt kĂŠt nemnegatĂv egĂŠsz szĂĄmpĂĄr tesz eleget: x=0, y=2 ĂŠs x=9, y=11.
B.3776. Az ABCD hĂşrnĂŠgyszĂśg BD ĂĄtlĂłja egyben a kĂśrĂźlĂrt kĂśr ĂĄtmĂŠrĹje. Az ABC hĂĄromszĂśg oldalainak a hossza legalĂĄbb 1. BizonyĂtsuk be, hogy a nĂŠgyszĂśg terĂźlete nagyobb, mint \(\displaystyle \frac{1}{2}\) terĂźletegysĂŠg.
(4 pont)
Klein Eszter ĂŠs Terry Tao (Sidney, AusztrĂĄlia)
MegoldĂĄs: ThalĂŠsz tĂŠtele miatt az ABD ĂŠs CBD hĂĄromszĂśgek A illetve C csĂşcsĂĄnĂĄl derĂŠkszĂśg van. A nĂŠgyszĂśg T terĂźlete e kĂŠt hĂĄromszĂśg terĂźletĂŠnek Ăśsszege. FelhasznĂĄlva, hogy AB,AC,BC\(\displaystyle \ge\)1, a hĂĄromszĂśg egyenlĹtlensĂŠg miatt
\(\displaystyle T={1\over2}(AB\cdot AD+BC\cdot CD)\ge{1\over2}(AD+CD\){1\over2}AC\ge {1\over2}.">
B.3777. Az ABC egyenlĹ szĂĄrĂş hĂĄromszĂśg szĂĄrszĂśge BAC\(\displaystyle \angle\)=\(\displaystyle \alpha\). A BC alapot B-tĹl C felĂŠ haladva n egyenlĹ rĂŠszre osztĂł pontok D1, D2,..., Dn-1. Az AB szĂĄrat 1:(n-1) arĂĄnyban osztĂł pont E. Igazoljuk, hogy
\(\displaystyle AD_1E\sphericalangle+AD_2E\sphericalangle+\dots+AD_{n-1}E\sphericalangle= \frac{\alpha}{2}. \)
(4 pont)
MegoldĂĄs: JelĂślje i=1,2,..., n-1 esetĂŠn a BADi, ADiE ĂŠs BEDi szĂśgeket redre \(\displaystyle \alpha\)i, \(\displaystyle \delta\)i, \(\displaystyle \varepsilon\)i. Egy hĂĄromszĂśg kĂŠt belsĹ szĂśgĂŠnek Ăśsszege egyenlĹ a harmadik csĂşcsnĂĄl lĂŠvĹ kĂźlsĹ szĂśggel. Ezt az ADiE hĂĄromszĂśgre alkalmazva az \(\displaystyle \alpha\)i+\(\displaystyle \delta\)i=\(\displaystyle \epsilon\)i ĂśsszefĂźggĂŠst kapjuk, ahonnan
\(\displaystyle \sum_{i=1}^{n-1}AD_iE\measuredangle=\sum_{i=1}^{n-1}\delta_i= \sum_{i=1}^{n-1}\varepsilon_i-\sum_{i=1}^{n-1}\alpha_i.\)
A pĂĄrhuzamos szelĹk tĂŠtele miatt a BEDn-1 hĂĄromszĂśg hasonlĂł a BAC hĂĄromszĂśghĂśz, tehĂĄt egyenlĹszĂĄrĂş ĂŠs szĂĄrszĂśge \(\displaystyle \varepsilon\)n-1=\(\displaystyle \alpha\). A hĂĄromszĂśgek ĂŠs a felosztĂĄs szimmetriĂĄja miatt 1\(\displaystyle \le\)i\(\displaystyle \le\)n-2 esetĂŠn felĂrhatĂłk az
\(\displaystyle \varepsilon\)i+\(\displaystyle \varepsilon\)n-1-i=\(\displaystyle \alpha\)
ĂŠs 1\(\displaystyle \le\)i\(\displaystyle \le\)n-1 esetĂŠn az
\(\displaystyle \alpha\)i+\(\displaystyle \alpha\)n-i=\(\displaystyle \alpha\)
egyenlĹsĂŠgek, ahonnan
\(\displaystyle \sum_{i=1}^{n-2}\varepsilon_i={n-2\over2}\alpha,\quad\sum_{i=1}^{n-1}\alpha_i={n-1\over2}\alpha.\)
MegĂĄllapĂtĂĄsainkat Ăśsszegezve,
\(\displaystyle \sum_{i=1}^{n-1}AD_iE\measuredangle=\sum_{i=1}^{n-2}\varepsilon_i+ \varepsilon_{n-1}-\sum_{i=1}^{n-1}\alpha_i= {n-2\over2}\alpha+\alpha-{n-1\over2}\alpha={\alpha\over2},\)
ahogyan azt bizonyĂtanunk kellett.
B.3778. Az ABCD konvex nĂŠgyszĂśg ĂĄtlĂłi az E pontban metszik egymĂĄst. Igazoljuk, hogy
\(\displaystyle \big|t(ABE\triangle)-t(CDE\triangle)\big|\le\frac{1}{2}AD\cdot BC. \)
(4 pont)
MegoldĂĄs: Az E pontbĂłl az A,B,C,D csĂşcsokba mutatĂł vektorokat jelĂślje rendre a, b, c ĂŠs d. Ekkor az axb ĂŠs cxd vektorok irĂĄnya megegyezik, hosszuk pedig rendre az ABE illetve CDE hĂĄromszĂśgek terĂźletĂŠnek kĂŠtszeresĂŠvel egyenlĹ. Vagyis
2|t( ABE\(\displaystyle \Delta\)) - t( CDE\(\displaystyle \Delta\))| = |axb-cxd|.
Mivel az a ĂŠs c vektorok pĂĄrhuzamosak, axc=0, ĂŠs ugyanĂgy dxb is a nullvektor lesz. EzĂŠrt
\(\displaystyle AD\cdot BC\ge\left|\overrightarrow{AD}\times\overrightarrow{BC}\right| =\left|(d-a)\times(c-b)\right|=\left|d\times c-a\times c-d\times b+a\times b\right|= \left|a\times b-c\times d\right|,\)
bizonyĂtva az ĂĄllĂtĂĄst.
B.3779. TekintsĂźk azokat a sĂkokat, amelyek a 2 egysĂŠg ĂŠlĹą kocka egy-egy csĂşcsĂĄbĂłl kiindulĂł ĂŠlek felezĹpontjĂĄn mennek ĂĄt. Mekkora a sĂkok ĂĄltal hatĂĄrolt konvex test tĂŠrfogata?
(3 pont)
MegoldĂĄs: A sĂkok a kocka minden egyes csĂşcsĂĄbĂłl levĂĄgnak egy-egy egymĂĄsba nem nyĂşlĂł tetraĂŠdert. Egy ilyen tetraĂŠdernek hĂĄrom egy csĂşcsban ĂśsszefutĂł egymĂĄsra merĹleges ĂŠle egysĂŠgnyi hosszĂş, a tetraĂŠder tĂŠrfogata tehĂĄt 1/6. A megcsonkĂtott kocka tĂŠrfogata tehĂĄt 8-8(1/6)=40/6 egysĂŠgnyi.
TekintsĂźk most az eredeti kocka egy lapjĂĄt (mondjuk a felsĹ lapot, amenynyiben a kockĂĄt az egyik lapjĂĄra ĂĄllĂtottuk), ebbĹl a sĂkok egy olyan nĂŠgyzetet vĂĄgnak ki, melynek csĂşcsai a lap ĂŠleinek felezĹpontjai; e nĂŠgyzet terĂźlete fele a lap terĂźletĂŠnek, tehĂĄt 2 egysĂŠgnyi. A nĂŠgyzet tetszĹleges e ĂŠlĂŠt kivĂĄlasztva, az arra illeszkedĹ elvĂĄgĂł S sĂk ĂĄthalad a nĂŠgyzetlap kĂśzĂŠppontja fĂślĂśtt 1 egysĂŠg tĂĄvolsĂĄgra elhelyezkedĹ ponton. Ezt Ăşgy lĂĄthatjuk be, hogy tekintjĂźk a kockĂĄnak azt az ĂŠlkĂśzĂŠppontjĂĄt, mely az S sĂkra illeszkedik ĂŠs az e ĂŠllel egy szabĂĄlyos hĂĄromszĂśget alkot. Ezt a pontot az e ĂŠl egyenesĂŠre tĂźkrĂśzve kapjuk az elĹbb emlĂtett pontot, mely nyilvĂĄn illeszkedik az S sĂkra. Az elvĂĄgĂł sĂkok a kocka felsĹ lapjĂĄval egyĂźtt tehĂĄt egy olyan nĂŠgyzet alapĂş egyenes gĂşlĂĄt hatĂĄroznak meg, melynek alapterĂźlete 2 egysĂŠgnyi, magassĂĄga 1 egysĂŠgnyi, tĂŠrfogata pedig ennek megfelelĹen 2/3.
A sĂkok ĂĄltal hatĂĄrolt test (mely egyĂŠbkĂŠnt egy szabĂĄlyos oktaĂŠder lesz) tĂŠrfogatĂĄt tehĂĄt megkapjuk, ha a megcsonkĂtott kocka tĂŠrfogatĂĄhoz hozzĂĄdjuk a kocka lapjaira emelt hat kis gĂşla tĂŠrfogatĂĄt. Az eredmĂŠny ezek szerint
\(\displaystyle {40\over6}+6\cdot{2\over3}={64\over6}.\)
B.3780. Igazoljuk, hogy az x, y, z pozitĂv szĂĄmokra teljesĂźl az alĂĄbbi egyenlĹtlensĂŠg:
\(\displaystyle \frac{x+y+z}{\sqrt[3]{xyz}}\le\frac{x}{y}+\frac{y}{z}+\frac{z}{x}. \)
(5 pont)
Elemente der Mathematik, Basel
MegoldĂĄs: Az \(\displaystyle a=x/\root3\of{xyz}\), \(\displaystyle b=y/\root3\of{xyz}\), \(\displaystyle c=z/\root3\of{xyz}\) helyettesĂtĂŠssel az a,b,c pozitĂv szĂĄmokra abc=1 teljesĂźl, egyenlĹtlensĂŠgĂźnk pedig az
\(\displaystyle {a\over b}+{b\over c}+{c\over a}\geq a+b+c\)
alakot Ăślti. Az ĂĄltalĂĄnossĂĄg megszorĂtĂĄsa nĂŠlkĂźl feltehetĹ, hogy a hĂĄrom szĂĄm kĂśzĂźl a a legnagyobb, b pedig a legkisebb; ekkor a\(\displaystyle \ge\)1\(\displaystyle \ge\)b ĂŠs \(\displaystyle \alpha\)=ab\(\displaystyle \le\)a. ElvĂŠgezve a c=1/ab helyettesĂtĂŠst, egyenlĹtlensĂŠgĂźnk Ăgy alakĂthatĂł:
\(\displaystyle {a\over b}+ab^2+{1\over a^2b}\ge a+b+{1\over ab},\)
vagy ami ezzel ekvivalens:
a3+a3b3+1\(\displaystyle \ge\)a3b+a2b2+a.
Az \(\displaystyle \alpha\)=ab helyettesĂtĂŠssel tehĂĄt az
a3+\(\displaystyle \alpha\)3+1-\(\displaystyle \alpha\)a2-\(\displaystyle \alpha\)2-a\(\displaystyle \ge\)0
egyenlĹtlensĂŠget kell igazolnunk. Itt a baloldali kifejezĂŠst
(a2-1)(a-\(\displaystyle \alpha\)) + (\(\displaystyle \alpha\)2-1)(\(\displaystyle \alpha\)-1)
alakra hozahtjuk. Az a\(\displaystyle \ge\)1 ĂŠs a\(\displaystyle \ge\) egyenlĹtlensĂŠgek miatt (a2-1)(a-
egyenlĹtlensĂŠgek miatt (a2-1)(a- )
) 0, ahol egyenlĹsĂŠg a=1 vagy a=
0, ahol egyenlĹsĂŠg a=1 vagy a= esetĂŠn ĂĄll fenn. TovĂĄbbĂĄ
esetĂŠn ĂĄll fenn. TovĂĄbbĂĄ
( 2-1)(
2-1)( -1)=(
-1)=( -1)2(
-1)2( +1)
+1) 0,
0,
itt egyenlĹsĂŠg  =1 esetĂŠn ĂĄll fenn.
=1 esetĂŠn ĂĄll fenn.
Ezzel az egyenlĹtlensĂŠget igazoltuk. EgyenlĹsĂŠg esetĂŠn szĂźksĂŠgkĂŠppen  =1, ahonnan a=1 is adĂłdik, ebbĹl pedig b=1, majd c=1 is kĂśvetkezik. Mivel ekvivalens ĂĄtalakĂtĂĄsokat hajtottunk vĂŠgre, az eredeti egyenlĹtlensĂŠgben x=y=z esetĂŠn ĂĄllhat csak fenn egyenlĹsĂŠg, amikor is mindkĂŠt oldal ĂŠrtĂŠke 3-mal egyenlĹ.
=1, ahonnan a=1 is adĂłdik, ebbĹl pedig b=1, majd c=1 is kĂśvetkezik. Mivel ekvivalens ĂĄtalakĂtĂĄsokat hajtottunk vĂŠgre, az eredeti egyenlĹtlensĂŠgben x=y=z esetĂŠn ĂĄllhat csak fenn egyenlĹsĂŠg, amikor is mindkĂŠt oldal ĂŠrtĂŠke 3-mal egyenlĹ.
B.3781. HatĂĄrozzuk meg a 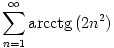 Ăśsszeg ĂŠrtĂŠkĂŠt.
Ăśsszeg ĂŠrtĂŠkĂŠt.
(5 pont)
MegoldĂĄs: Legyen  n=arcctg(2n2), ekkor 0<
n=arcctg(2n2), ekkor 0< n<
n<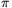 /4 ĂŠs tan
/4 ĂŠs tan  n=1/2n2. Legyen
n=1/2n2. Legyen  1+
1+ 2+...+
2+...+ n=
n=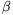 n. Ekkor tan
n. Ekkor tan 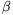 1=1/2, ĂŠs a tangens fĂźggvĂŠny addĂciĂłs kĂŠplete segĂtsĂŠgĂŠvel tan
1=1/2, ĂŠs a tangens fĂźggvĂŠny addĂciĂłs kĂŠplete segĂtsĂŠgĂŠvel tan 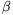 n nĂŠhĂĄny tovĂĄbbi ĂŠrtĂŠkĂŠt is kiszĂĄmĂthatjuk: tan
n nĂŠhĂĄny tovĂĄbbi ĂŠrtĂŠkĂŠt is kiszĂĄmĂthatjuk: tan 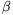 2=2/3, tan
2=2/3, tan 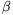 3=3/4, tan
3=3/4, tan 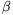 4=4/5. TegyĂźk fel tehĂĄt, hogy n
4=4/5. TegyĂźk fel tehĂĄt, hogy n 2 ĂŠs a tan
2 ĂŠs a tan 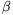 n-1=1-1/n ĂśsszefĂźggĂŠst mĂĄr igazoltuk. Ekkor
n-1=1-1/n ĂśsszefĂźggĂŠst mĂĄr igazoltuk. Ekkor
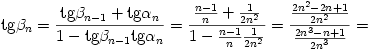
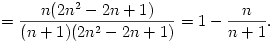
A teljes indukciĂł elve szerint tehĂĄt minden n pozitĂv egĂŠsz szĂĄmra tan 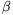 n=1-1/(n+1). Tudjuk tovĂĄbbĂĄ, hogy 0<
n=1-1/(n+1). Tudjuk tovĂĄbbĂĄ, hogy 0<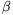 1<
1<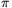 /4. Ha n
/4. Ha n 2 ĂŠs 0<
2 ĂŠs 0<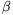 n-1<
n-1<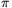 /4, akkor 0<
/4, akkor 0<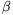 n=
n=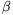 n-1+
n-1+ n<
n<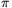 /2 ĂŠs tan
/2 ĂŠs tan 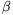 n<1 miatt 0<
n<1 miatt 0<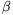 n<
n<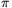 /4 is teljesĂźl. A
/4 is teljesĂźl. A 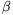 n sorozat Ăśsszes eleme tehĂĄt 0 ĂŠs
n sorozat Ăśsszes eleme tehĂĄt 0 ĂŠs 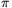 /4 kĂśzĂŠ esik, tovĂĄbbĂĄ tan
/4 kĂśzĂŠ esik, tovĂĄbbĂĄ tan 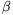 n szigorĂşan nĂśvekedĹ mĂłdon 1-hez tart. Minthogy pedig a tangens fĂźggvĂŠny a (0,
n szigorĂşan nĂśvekedĹ mĂłdon 1-hez tart. Minthogy pedig a tangens fĂźggvĂŠny a (0,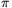 /2) intervallumban szigorĂşan monoton nĂśvekedĹ folytonos fĂźggvĂŠny, megĂĄllapĂthatjuk, hogy a
/2) intervallumban szigorĂşan monoton nĂśvekedĹ folytonos fĂźggvĂŠny, megĂĄllapĂthatjuk, hogy a 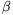 n sorozat hatĂĄrĂŠrtĂŠke
n sorozat hatĂĄrĂŠrtĂŠke 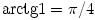 . A feladatban szereplĹ vĂŠgtelen Ăśsszeg tehĂĄt konvergens, ĂŠrtĂŠke pedig
. A feladatban szereplĹ vĂŠgtelen Ăśsszeg tehĂĄt konvergens, ĂŠrtĂŠke pedig 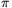 /4-gyel egyenlĹ.
/4-gyel egyenlĹ.