A KöMaL 2018. szeptemberi matematika feladatai

K-jelű feladatok A beküldési határidő 2018. október 10-én LEJÁRT.

---

K. 589. Egy cég egy vállalkozóval nyírat le egy adott nagyságú füves területet. A vállalkozó kiszállási díja alkalmanként 5000 Ft. Ha havonta háromszor kell lenyírnia a füvet, akkor 1,8-szer annyi pénzt kér el alkalmanként munkadíjként, mint ha havonta négyszer kell lenyírni, mert az első esetben nagyobb a fű, így többet kell vele dolgoznia. Ezen feltételek mellett a megbízó cégnek jobban megéri havonta négyszer nyíratni a füvet, mint havonta háromszor. Legalább hány forint az egy alkalomra eső munkadíj havi négyszeri nyírás esetén? (Az egy alkalomra eső munkadíj havi 4 nyírás esetén 100 Ft-ra kerek összeg.)

(6 pont)

megoldás, statisztika

---

K. 590. András, Béla és Csaba egy futóversenyen vettek részt. A verseny végén az derült ki, hogy András a célba érkezésekor 15 méterrel verte Bélát, és 35 méterrel verte Csabát, Béla pedig a célba érkezésekor 22 méterrel verte Csabát. Hány méter volt a futóverseny távja, ha a három fiú végig egyenletes tempóban futott a versenyen?

(6 pont)

megoldás, statisztika

---

K. 591. Egy gyerekcsapat egy buszos kiránduláson vesz részt. A buszban 52 ülés van, amiből kettőn a tanárok ülnek. A maradék helyeken vagy egy gyerek ül, vagy a csomagja van. A busz csomagtartójába a gyerekek egyharmadának a csomagja fért be. Hányan voltak a kiránduló gyerekek, ha a buszban minden ülés maximálisan ki volt használva?

(6 pont)

megoldás, statisztika

---

K. 592. Anna, Bea és Cili együtt dolgoznak egy munkán. Együtt 6 órával kevesebb idő alatt végeznek, mintha Anna egyedül dolgozott volna, 1 órával korábban végeznek, mint ha Bea egyedül dolgozott volna, és feleannyi idő alatt végeznek, mint ha Cili egyedül dolgozott volna. Ha Anna és Bea Cili nélkül dolgozna, akkor 80 perc alatt végeznének. Hány perc alatt végezné el a munkát Anna, illetve Bea külön-külön?

(6 pont)

megoldás, statisztika

---

K. 593. Egy renitens osztály bojkottálni akarja a testnevelés órát, ezért a kislabhajításnál arra törekszenek, hogy a labdákat átdobják a kerítésen, és a labdák begyűjtéséig álljon az óra. Az osztály 1/6 része 5-5 labdát dob, fele 4-4 labdát, 1 tanuló 6 labdát, a többiek pedig 2-2 labdát. A labdák 75%-át sikerült is átdobni a kerítésen. Elég sok idő elment azzal, hogy mind a 66 kirepült labdát összeszedték, ezért a tanár büntetésből fejenként 3-3 kört futtatott az osztállyal a 200 méteres futópályán. Hány km-t futottak összesen a renitens osztály tanulói?

(6 pont)

megoldás, statisztika

C-jelű feladatok A beküldési határidő 2018. október 10-én LEJÁRT.

---

C. 1490. Milyen maradékot ad az \(\displaystyle N=863\underbrace{99\ldots 9}_\text{2018 db}\) (ahol a szám végén \(\displaystyle 2018\) db \(\displaystyle 9\)-es számjegy áll) \(\displaystyle 32\)-vel osztva?

(5 pont)

megoldás, statisztika

---

C. 1491. Az \(\displaystyle ABCD\) téglalap \(\displaystyle AD\) oldala \(\displaystyle 1\) cm hosszú. A \(\displaystyle BAD\) szög szögfelezője és az \(\displaystyle AC\) átló felező merőlegese a \(\displaystyle CD\) oldalon metszi egymást. Adjuk meg a \(\displaystyle CD\) oldal pontos értékét.

(5 pont)

megoldás, statisztika

---

C. 1492. Hányféleképpen juthatunk el az ábrán látható 15 egységkockából felépített test \(\displaystyle A\) csúcsából a \(\displaystyle B\) csúcsába rácsvonalak mentén, ha csak a három megjelölt irányba haladhatunk?

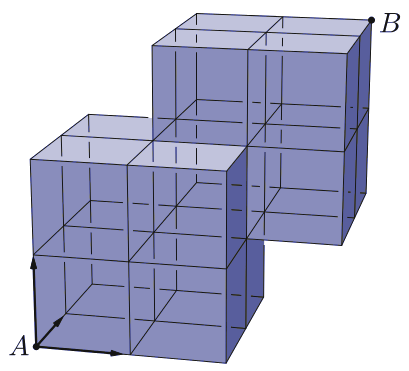
(5 pont)

megoldás, statisztika

---

C. 1493. Az egységnyi területű háromszög \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) oldalaira fennáll: \(\displaystyle a\ge b\ge c\). Mutassuk meg, hogy \(\displaystyle b\ge \sqrt2\,\).

(5 pont)

megoldás, statisztika

---

C. 1494. Bizonyítsuk be, hogy ha \(\displaystyle p\) és \(\displaystyle q\) \(\displaystyle 3\)-nál nagyobb ikerprímek, akkor számtani közepük osztható \(\displaystyle 6\)-tal, a szorzatukat \(\displaystyle 1\)-gyel növelve pedig \(\displaystyle 36\)-tal osztható számot kapunk.

(5 pont)

megoldás, statisztika

---

C. 1495. Tekintsük az alábbi egyenlőségsorozatot:

$$\begin{align*} 1 + 2 & = 3, \tag{1}\\ 4 + 5 + 6 & = 7 + 8, \tag{2}\\ 9 + 10 + 11 + 12 & = 13 + 14 + 15. \tag{3} \end{align*}$$

A megfigyelt szabály alapján írjuk fel a \(\displaystyle k\)-adik sort és bizonyítsuk annak helyességét.

Javasolta: Kertész Ádám (Miami Beach)

(5 pont)

megoldás, statisztika

---

C. 1496. Egy háromszög csúcsai körül vett 1, 2, illetve 3 cm sugarú körök páronként kívülről érintik egymást. Mekkora területet nem fednek le a körök a háromszögből?

(5 pont)

megoldás, statisztika

B-jelű feladatok A beküldési határidő 2018. október 10-én LEJÁRT.

---

B. 4966. Határozzuk meg a 19. legkisebb olyan pozitív egész számot, amelyben a számjegyek összege 2018.

(3 pont)

megoldás, statisztika

---

B. 4967. Az \(\displaystyle ABC\triangle\) belső pontja \(\displaystyle P\), az \(\displaystyle AB\) oldal felezőpontja \(\displaystyle C_1\), a \(\displaystyle BC\) oldalé \(\displaystyle A_1\), a \(\displaystyle CA\) oldalé \(\displaystyle B_1\). Húzzunk párhuzamosokat rendre az \(\displaystyle AP\), \(\displaystyle BP\) és \(\displaystyle CP\) egyenesekkel az \(\displaystyle A_1\), \(\displaystyle B_1\), illetve \(\displaystyle C_1\) pontokon keresztül. Mutassuk meg, hogy ez a három egyenes egy pontban metszi egymást.

Javasolta: Kozma József (Szeged)

(3 pont)

megoldás, statisztika

---

B. 4968. Oldjuk meg a következő egyenletrendszert a pozitív valós számok halmazán:

$$\begin{align*} \frac{1}{1+a + ab + abc} + \frac{1}{1+b + bc + bcd} + \frac{1}{1+c + cd + cda} + \frac{1}{1+d + da + dab} & = 1,\\ a+b+c+d & = 4. \end{align*}$$

(4 pont)

megoldás, statisztika

---

B. 4969. A \(\displaystyle T\) téglalap oldalai \(\displaystyle a\le b\). Tudjuk, hogy valamely két \(\displaystyle r\) sugarú kör együttesen lefedi \(\displaystyle T\)-t, valamint azt is tudjuk, hogy két \(\displaystyle r\)-nél kisebb sugarú körrel ez nem lehetséges. Határozzuk meg \(\displaystyle r\)-t.

(4 pont)

megoldás, statisztika

---

B. 4970. Adott a síkon két pont \(\displaystyle A\) és \(\displaystyle B\), továbbá egy ezeket elválasztó \(\displaystyle e\) egyenes. Válasszunk az \(\displaystyle e\) egyenesen \(\displaystyle P\) és \(\displaystyle Q\) pontokat úgy, hogy \(\displaystyle PAQ\sphericalangle=90^{\circ}\) teljesüljön. Mutassuk meg, hogy létezik egy olyan, \(\displaystyle B\)-től különböző pont, amelyen a \(\displaystyle B\), \(\displaystyle P\) és \(\displaystyle Q\) pontokra illeszkedő kör — a \(\displaystyle P\) és \(\displaystyle Q\) pontok választásától függetlenül — áthalad.

Javasolta: 11. C. osztály, Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn.

(5 pont)

megoldás, statisztika

---

B. 4971. Milyen \(\displaystyle p\) prímszámokhoz létezik olyan \(\displaystyle a\) pozitív egész, amelyre

\(\displaystyle 1+a+a^2+\ldots+a^{p-1} \)

osztható \(\displaystyle p^2\)-tel?

(5 pont)

megoldás, statisztika

---

B. 4972. Az \(\displaystyle ABC\) hegyesszögű háromszög belső \(\displaystyle P\) pontjának az oldalakra vett merőleges vetületei az ábra szerint \(\displaystyle D\), \(\displaystyle E\) és \(\displaystyle F\). Az oldalakon keletkező hat szakaszra kifelé négyzeteket rajzolunk, amiket felváltva két színnel színezünk az ábra szerint. Az azonos színű négyzetek ,,külső'' oldalegyenesei egy-egy háromszöget határoznak meg. Mutassuk meg, hogy ez a két háromszög egybevágó.

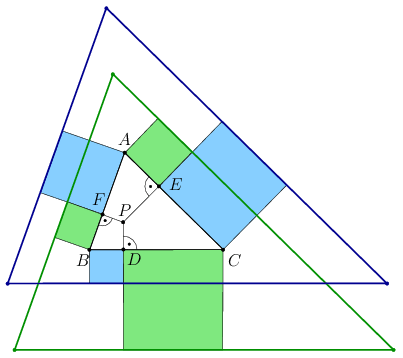
(6 pont)

megoldás, statisztika

---

B. 4973. Legyenek \(\displaystyle a_1, a_2, \ldots, a_{2018}\) olyan nemnegatív valós számok, amelyek összege \(\displaystyle 1\). Adjuk meg az

\(\displaystyle S = \sum_{i \ne j,\; i\mid j} a_ia_j \)

összeg lehető legnagyobb értékét.

(Argentin feladat alapán)

(6 pont)

megoldás, statisztika

A-jelű feladatok A beküldési határidő 2018. október 10-én LEJÁRT.

---

A. 728. Egy bolha ugrál a pozitív egész számokon. Első nap tetszőleges pozitív egészre ugorhat. Ezután minden nap átugrik egy olyan számra, amely legfeljebb kétszerese az előző napi állomáshelyének.

a) Mutassuk meg, hogy a bolha megtehet végtelen sok ugrást úgy, hogy soha ne érkezzen olyan számra, amelynek a tízes számrendszerbeli jegyeinek összege megegyezik egy korábbi állomáshelyén vett jegyösszeggel.

b) Tud-e így ugrálni, ha a számok kettes számrendszerbeli alakjában vizsgáljuk a számjegyek összegét?

Dürer verseny, 2015

(7 pont)

statisztika

---

A. 729. Az \(\displaystyle ABCD\) húrnégyszög átlóinak metszéspontja \(\displaystyle E\), az \(\displaystyle AB\) oldal felezőpontja \(\displaystyle F\), és az \(\displaystyle E\) pont merőleges vetületei a \(\displaystyle DA\), \(\displaystyle AB\) és \(\displaystyle BC\) egyeneseken rendre \(\displaystyle P\), \(\displaystyle Q\), illetve \(\displaystyle R\). Igazoljuk, hogy a \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\) és \(\displaystyle F\) pontok egy körre illeszkednek.

Javasolta: Weisz Máté (Szeged)

(7 pont)

megoldás, statisztika

---

A. 730. Legyen \(\displaystyle F_n\) az \(\displaystyle n\)-edik Fibonacci-szám (\(\displaystyle {F_1=F_2=1}\), \(\displaystyle {F_{n+1}=F_n+F_{n-1}}\)). Konstruáljunk végtelen sok olyan \(\displaystyle n\) pozitív egész számot, amelyre \(\displaystyle F_{F_n}\) osztható \(\displaystyle n\)-nel, de \(\displaystyle F_n\) nem osztható \(\displaystyle n\)-nel.

(7 pont)

megoldás, statisztika