A KöMaL 2019. februári fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2019. március 11-én LEJÁRT. |
M. 384. Határozzuk meg egy ismert teljesítményű elektromos vízforraló kancsó hatásfokát a benne lévő víz tömegének függvényében!
Közli: Nagy Piroska Mária, Budapest
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2019. március 11-én LEJÁRT. |
G. 661. Egyenes mérőhengerbe három, egymással nem keveredő folyadékot öntünk: 1000 kg/m\(\displaystyle {}^3\) sűrűségű 100 g vizet, 0,8 g/cm\(\displaystyle {}^3\) sűrűségű 200 g olajat, és annyi higanyt, hogy tele legyen a 400 cm\(\displaystyle {}^3\) térfogatú, 40 cm magas mérőhenger. Hány gramm higanyt öntöttünk a mérőhengerbe? Milyen magasságban helyezkednek el a folyadékokat egymástól elválasztó határrétegek a henger aljától számítva? (A higany sűrűsége \(\displaystyle 13\,600\) kg/m\(\displaystyle {}^3\).)
(3 pont)
G. 662. Az \(\displaystyle (a)\) és a \(\displaystyle (b)\) ábrán látható összeállítás egy nagyobb korongból és egy-egy, hozzá koncentrikusan rögzített, kisebb hengerből áll. A kis hengerekre fonalakat csévéltünk, amelyeknek végét egy rúd segítségével vízszintesen, \(\displaystyle v\) sebességgel mozgatjuk.
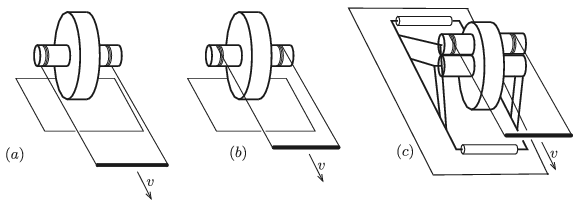
A \(\displaystyle (c)\) esetben a kis hengerhez felülről egy vele azonos átmérőjű, szabadon forgó másik kis henger is csatlakozik. A felső henger nekiszorul az alsónak, és a lebillenését egy-egy görgőhöz csatlakozó rúdszerkezet akadályozza meg. A felső hengerre is fonalat csévéltünk, és a fonál végét \(\displaystyle v\) sebességgel húzzuk. A korongok a talajon, illetve a kis hengerek egymáson nem csúsznak meg.
Melyik irányban, és \(\displaystyle v\)-nél nagyobb vagy kisebb sebességgel fog mozogni a korong középpontja az egyes esetekben?
(3 pont)
G. 663. Az ábrán két izzólámpa, egy zsebtelep és egy olyan kettős kapcsoló látható, amely egyszerre vált át két érintkezőt. Tervezzünk a megadott eszközökből olyan áramkört (vagyis rajzoljuk meg a vezetékeket), hogy a kapcsoló egyik állásában a két lámpa sorosan, a másik állásában párhuzamosan legyen bekötve!
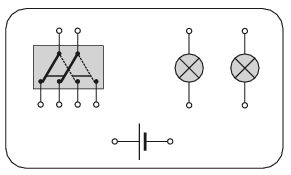
(3 pont)
G. 664. Az év azonos napjára eső újholdkor vagy teliholdkor vagyunk közelebb a Naphoz? Becsüljük meg, hogy mekkora a kétféle távolságunk különbsége!
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2019. március 11-én LEJÁRT. |
P. 5100. Két ágyúval pontosan ugyanabban a pillanatban tüzelnek egymás felé az ábrán látható \(\displaystyle A\) és \(\displaystyle B\) pontból. Az \(\displaystyle A\) ágyú lövedékének torkolati sebessége 40 m/s, míg a \(\displaystyle B\) ágyúé 60 m/s. Eltalálják-e a lövedékek egymást? Ha igen, akkor hol és mikor? Ha nem, akkor hol csapódnak be a talajba?
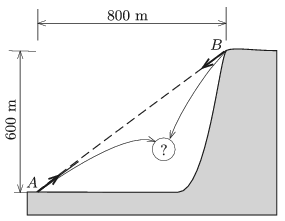
Amerikai feladat
(4 pont)
P. 5101. Egy űrhajó körpályán kering a Föld körül, keringési ideje 100 perc. A Föld felszínének mekkora részét láthatja az űrhajós egy adott pillanatban? (A légköri fénytörést elhanyagolhatjuk.)
Némedi István (1932–1998) feladata nyomán
(4 pont)
P. 5102. Vízszintes talajon \(\displaystyle m_1\) tömegű kiskocsi \(\displaystyle v_0\) sebességgel halad az álló, \(\displaystyle m_2\) tömegű kiskocsi felé. Mindkét kocsin egy-egy \(\displaystyle m\) tömegű, lapos hasáb van. A hasábok és a kiskocsik felülete közötti tapadási súrlódási együttható \(\displaystyle \mu_0\). Az álló kiskocsin \(\displaystyle D\) rugóállandójú nyomórugó van.
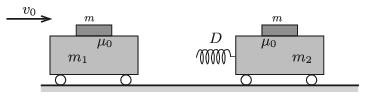
Ütközéskor megcsúszik-e valamelyik hasáb?
Adatok: \(\displaystyle m_1=0{,}2~\rm kg\); \(\displaystyle m_2=m=0{,}1~\rm kg\); \(\displaystyle \mu_0=0{,}5\); \(\displaystyle D=12~\rm N/m\); \(\displaystyle v_0=1~\rm m/s\).
Közli: Németh László, Fonyód
(4 pont)
P. 5103. Egyik végénél felfüggesztett, függőlegesen szabadon lógó, \(\displaystyle m\) tömegű SLINKY-rugó a saját súlya alatt \(\displaystyle L\) hosszúságúra nyúlik. Ezután a rugó egyik végét \(\displaystyle H\) magasságban egy vízszintes asztallap felett tartjuk \(\displaystyle (H<L)\), így a rugó nem tud teljesen kinyúlni. Mekkora erő hat a rugóra a felfüggesztésnél, illetve az alátámasztásnál? (A rugó feszítetlen hossza \(\displaystyle H\)-hoz képest elhanyagolható.)
Közli: Gnädig Péter, Vácduka
(5 pont)
P. 5104. Dugattyúval lezárt edényben nitrogéngáz van. A dugattyút lassan kihúzva kissé csökkentjük a gáz nyomását. Mekkora a gáz moláris hőkapacitása, ha a térfogat 1%-os növekedése esetén a nyomás változása 0,5%?
Tornyai Sándor fizikaverseny, Hódmezővásárhely
(4 pont)
P. 5105. Három, vákuumban lévő, \(\displaystyle R\) sugarú fémgömb középpontja egy egyenesre esik. A középső gömb távolsága a másik két gömbtől \(\displaystyle d\gg R\). A szélső gömbök hőmérséklete állandó, az egyiké \(\displaystyle T_1\), a másiké \(\displaystyle T_2\). Mekkora a középső gömb állandósult hőmérséklete, ha a gömbök abszolút fekete testeknek tekinthetők?
Közli: Simon Péter, Pécs
(5 pont)
P. 5106. Egyenlő oldalú háromszög keresztmetszetű, \(\displaystyle n_1=1{,}8\) abszolút törésmutatójú prizmára vékony fénysugarat bocsátunk úgy, hogy a fénysugár pályája a felezősíkra szimmetrikus legyen.
\(\displaystyle a)\) Mekkora a belépő fénysugár beesési szöge?
\(\displaystyle b)\) Mekkora a belépő sugár és a kilépő sugár közötti szög, az ún. deviáció?
\(\displaystyle c)\) Ezután az egymáshoz képest rögzített prizma-fényforrás rendszert egy \(\displaystyle {n_2=1{,}5}\) törésmutatójú folyadékba merítjük. Mekkora lesz ebben az esetben a deviáció?
Közli: Holics László, Budapest
(5 pont)
P. 5107. Öt egyforma és egy különböző ellenállásból tetraéder alakú kapcsolást forrasztunk össze. Egyetlen ellenállásmérő műszer áll rendelkezésünkre, és a látszólag egyforma hat ellenállás kapcsolását nem szabad megbontanunk. Legfeljebb hány mérést kell elvégezzünk, hogy megtaláljuk a többitől eltérő értékű ellenállást, és még az ellenállások nagyságát is megtudjuk? Szerencsés esetben hány méréssel juthatunk el a megoldáshoz?
Pakisztáni feladat
(5 pont)
P. 5108. Mekkora az a legkisebb sebesség, amellyel az \(\displaystyle m\) tömegű, \(\displaystyle q\) töltésű testet vákuumban fellőve már eljut a függőlegesen fölötte \(\displaystyle \ell\) távolságban rögzített, \(\displaystyle Q\) töltésű testhez? (\(\displaystyle Q\) és \(\displaystyle q\) ellentétes előjelű töltések.)
Adatok: \(\displaystyle m=10^{-5}\) kg, \(\displaystyle q=4{,}0\cdot 10^{-9}\) C, \(\displaystyle Q= - 1{,}0\cdot 10^{-7}\) C, \(\displaystyle \ell=0{,}36~\)m.
Közli: Kobzos Ferenc, Dunaújváros
(5 pont)
P. 5109. Mekkora az elektron hullámhossza, ha a mozgási energiája
\(\displaystyle a)\) \(\displaystyle 1{,}75\cdot 10^{-16}~\)J;
\(\displaystyle b)\) 20 GeV?
Közli: Légrádi Imre, Sopron
(5 pont)
P. 5110. A Föld körül keringő két mesterséges hold pályájának fél nagytengelye ugyanakkora. A holdak pálya menti sebességeinek aránya a perigeumban (földközelpontban) \(\displaystyle \frac32\), és az itt nagyobb sebességű hold pályájának excentricitása 0,5.
Határozzuk meg pálya menti sebességük arányát az apogeumban (földtávolpontban), és számítsuk ki a másik mesterséges hold pályájának excentricitását!
Csillagászati versenyfeladat nyomán
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

