A KöMaL 2019. márciusi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2019. április 10-én LEJÁRT. |
M. 385. Ha a mosogatócsapból függőlegesen kifolyó vízsugár útjába egy viszonylag nagy kiterjedésű, vízszintes, sík akadályt helyezünk, akkor az azon elterülő víz egy kör mentén jól láthatóan megemelkedik. Ezt nevezik hidraulikus ugrásnak. Mérjük meg, hogy egy adott akadály-csap távolság esetén hogyan függ a kör sugara a vízhozamtól!
Közli: Szász Krisztián, Budapest
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2019. április 10-én LEJÁRT. |
G. 665. Vízszintes, súrlódásmentesnek tekinthető jégen csúszó, kis méretű korong mozgását vizsgáljuk. A jégből kiemelkedik egy négyzet keresztmetszetű oszlop, amelynek oldaléle 10 cm. A korong a felülnézeti ábrán látható módon van az oszlophoz rögzítve egy 1,0 m hosszú fonállal. A korongnak \(\displaystyle v=1{,}0\) m/s nagyságú kezdősebességet adunk. Mennyi idő múlva csapódik a korong az oszlophoz?

(3 pont)
G. 666. Az ábrán egy vidámparki szórakoztatószerkezet vázlata látható. A középső, nagy henger egyenletesen forog körbe. A rajta lévő négy rögzítőkar segítségével négy tengelyezett, kör alakú ,,gondola'' is körbejár. Minden gondola közepéhez egy-egy korongot rögzítettek, melyek ugyanúgy vannak tengelyezve, mint a gondola. A gondolák közepén lévő korongok csúszásmentes szíjáttétel segítségével csatlakoznak a szerkezet közepén található \(\displaystyle K\) koronghoz, ami rögzített, tehát egyáltalán nem forog. (Az ábrán – az áttekinthetőség kedvéért – csak az egyik gondolánál tüntettük fel ezt a szíjat.)
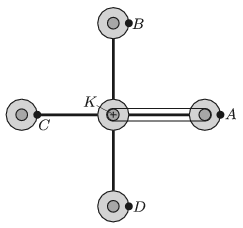
Az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\) pontok egy-egy utast ábrázolnak. Milyen pályán mozognak az utasok? Hogyan változik a közöttük lévő távolság a forgás közben? (A szerkezet vízszintes síkban forog, a tengelyek mind függőlegesek.)
Amerikai feladat nyomán
(4 pont)
G. 667. Mekkora nyomást fejt ki az asztalra helyezett 10 cm oldalélű alumíniumkocka? Hány százalékkal változik a nyomás, ha a kockát \(\displaystyle 20\;{}^\circ\)C-ról \(\displaystyle 100\;{}^\circ\)C-ra melegítjük? Növekszik vagy csökken a nyomás?
(3 pont)
G. 668. Nézzük meg a https://www.youtube.com/watch?v=hvqQ1XG1aQE videót! Egy megfelelően nagy gomb és egy vékony zsineg segítségével készítsük el a bemutatott játékot (zúgattyút), és próbáljuk ki. Miért jön gyors forgásba a gomb?
(3 pont)
 |
P-jelű feladatokA beküldési határidő 2019. április 10-én LEJÁRT. |
P. 5111. Függőlegesen feldobunk egy pingponglabdát. Vajon mi tart hosszabb ideig: a labda felfelé, vagy lefelé mozgása? (A légellenállás számottevő.)
Közli: Vigh Máté, Budapest
(3 pont)
P. 5112. Egy \(\displaystyle H\) magasságú falról \(\displaystyle v_0\) kezdősebességgel, a vízszintessel \(\displaystyle \alpha\) szöget bezáró irányban eldobtunk egy hógolyót. Ugyanebben a pillanatban mekkora és milyen irányú sebességgel indult el egy gyerek a faltól \(\displaystyle s\) távolságban lévő pontból, ha a hógolyó az egyenletesen, egyenes vonalban mozgó gyereket éppen eltalálta? (A légellenállást ne vegyük figyelembe! A mozgások egy, a falra merőleges síkban történnek.)
Adatok: \(\displaystyle H=45\) m, \(\displaystyle s=21\) m, \(\displaystyle v_0=5\) m/s, \(\displaystyle \alpha=30^\circ\).
Közli: Kobzos Ferenc, Dunaújváros
(4 pont)
P. 5113. Mennyit csökken méterenként egy 80 kg tömegű ember súlya, ha az Egyenlítőn épített toronyban halad felfelé?
Közli: Vass Miklós, Budapest
(4 pont)
P. 5114. Egy asztal peremére illeszkedik egy \(\displaystyle \alpha\) hajlásszögű lejtő, amelyről egy \(\displaystyle \ell\) hosszúságú, \(\displaystyle d\) magasságú, homogén anyageloszlású, téglatest alakú hasáb csúszik le. Mennyivel nyúlik túl a hasáb az asztal peremén, amikor elkezd lebillenni, ha
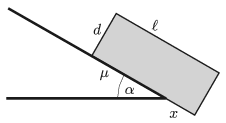
\(\displaystyle a)\) a hasáb és a lejtő közötti súrlódás elhanyagolható;
\(\displaystyle b)\) a hasáb és a lejtő közötti súrlódási együttható \(\displaystyle \mu\)? (\(\displaystyle 0<\mu<\tg\alpha\), és \(\displaystyle \mu d<\ell\).)
Közli: Honyek Gyula, Veresegyház
(5 pont)
P. 5115. Egy gömbszimmetrikus tömegeloszlású exobolygó tömege a Föld tömegének négyszerese, a nehézségi gyorsulás a – nem forgó – bolygó felszínén a földi érték kétszerese.
\(\displaystyle a)\) Mekkora a bolygó sugara és az átlagsűrűsége?
\(\displaystyle b)\) Mekkora a bolygón az első kozmikus sebesség?
Közli: Gnädig Péter, Vácduka
(5 pont)
P. 5116. \(\displaystyle R\) és \(\displaystyle 3R\) belső sugarú vezető gömbhéj egymástól távol helyezkedik el, falvastagságuk \(\displaystyle d\ll R\). A gömbök középpontjában \(\displaystyle 2Q\), illetve \(\displaystyle Q\) töltés van. Mekkora minimális munkával lehet ezeket a töltéseket felcserélni? (A falakon kis lyukak vannak.)
A Kvant nyomán
(5 pont)
P. 5117. Egy arany karikagyűrű éppen úgy helyezkedik el, hogy a földi mágneses indukcióvektor a gyűrű síkjával párhuzamos. A gyűrűt egyenletes forgómozgással 1 másodperc alatt \(\displaystyle 180^\circ\)-kal elfordítjuk. A forgástengely a gyűrű síkjába esik, és
\(\displaystyle a)\) a mágneses indukcióvektor irányával párhuzamos;
\(\displaystyle b)\) a mágneses indukcióvektor irányára merőleges.
Melyik esetben kell több munkát végeznünk a gyűrű megfordítása közben? Becsüljük meg, hogy mekkora lehet a kétféle munkavégzés közötti különbség!
Közli: Radnai Gyula, Budapest
(5 pont)
P. 5118. Egy \(\displaystyle \alpha=30^\circ\)-os hajlásszögű lejtőhöz két, egymástól \(\displaystyle \ell=10\) cm távolságra lévő, egymással párhuzamos, elhanyagolható ellenállású sín van rögzítve, melyeket az egyik végüknél állandó \(\displaystyle U_0\) feszültségű áramforrás kapcsol össze. A sínekre merőlegesen egy \(\displaystyle M=30\) g tömegű, \(\displaystyle R=0{,}2~\Omega\) ellenállású, vízszintes fémpálcát fektettünk, amely a síneken súrlódásmentesen mozoghat. A pálca közepéhez a sínekkel párhuzamos fonál csatlakozik, melynek elhanyagolható tömegű csigán átvetett függőleges darabjához egy \(\displaystyle m=50~\)g tömegű nehezék van erősítve. A berendezés függőlegesen lefelé mutató, \(\displaystyle B=0{,}5\) T indukciójú, homogén mágneses mezőben van.
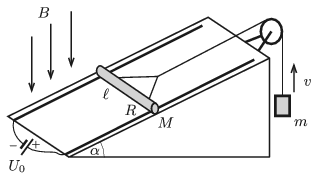
Mekkora legyen az áramforrás feszültsége, hogy az \(\displaystyle m\) tömegű nehezék
\(\displaystyle a)\) függőlegesen felfelé,
\(\displaystyle b)\) függőlegesen lefelé \(\displaystyle v=10~\)m/s sebességgel egyenletesen haladjon?
Közli: Zsigri Ferenc, Budapest
(5 pont)
P. 5119. Newton híres kísérletében (experimentum crucis) a fehér fényt színekre bontotta prizma segítségével. A színes fénysugarakat újra egyesítette fehér fénnyé. Megvalósítható-e a fehér fény felbontása és újraegyesítése a képen látható módon?
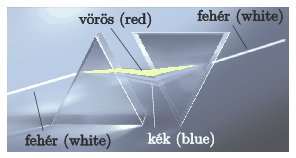
Az internet nyomán
(4 pont)
P. 5120. Sugárkezeléskor egy meghatározott dózist (tömegegységenként elnyelt energiát) kell eljuttatni a daganatba anélkül, hogy a környező egészséges szövetek túlságosan nagy dózisnak lennének kitéve. Vizsgáljuk ezt a problémát a következő egyszerű modellen. A beteg fejét egy 8 cm sugarú, homogén gömbnek tekintjük. A kis méretű daganat a gömb középpontjában van, és öt különböző átmérő irányából \(\displaystyle \gamma\)-fotonokkal sugározzuk be ugyanakkora intenzitással. A sugárnyaláb intenzitása (egységnyi felületre jutó teljesítménye) exponenciálisan csökken, ahogy a nyaláb áthalad a gömböt kitöltő szöveten az \(\displaystyle I(x)=I_0{\rm e}^{-\mu x}\) egyenletnek megfelelően.(Az \(\displaystyle x_0=\ln 2/\mu\) távolságot felező rétegvastagságnak nevezik; ennek számértéke függ a fotonok energiájától és az elnyelő közeg anyagától. 2,5 MeV-es fotonokra pl. vízben \(\displaystyle x_0=23\) cm.)

Kétféle sugárzást alkalmazhatunk: 1 MeV-es \(\displaystyle \gamma\)-fotonokat egy \(\displaystyle {}^{60}\)Co forrásból, ezekre \(\displaystyle \mu=0{,}07~\mathrm{cm}^{-1}\), vagy 6 MeV-es \(\displaystyle \gamma\)-fotonokat, amelyeket egy elektrongyorsítóval lehet létrehozni, itt \(\displaystyle \mu=0{,}028~\mathrm{cm}^{-1}\).
Melyik sugárzás kíméli jobban az egészséges szöveteket, azaz melyik eredményez kisebb dózist a gömb felületénél? Mekkora a dózis a gömb felületének közelében, ha a daganatnál a szükséges dózis értéke \(\displaystyle D\)?
Közli: Takács László, Baltimore, USA
(5 pont)
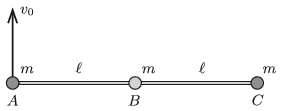
P. 5121. Három (\(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) jelű) kicsiny, egyforma, \(\displaystyle m\) tömegű golyó úgy van összekötve két elhanyagolható tömegű, \(\displaystyle \ell\) hosszúságú rúddal, hogy az egyik rúd az \(\displaystyle A\) és a \(\displaystyle B\) golyót, a másik rúd a \(\displaystyle B\) és a \(\displaystyle C\) golyót köti össze. A \(\displaystyle B\) golyónál a kapcsolódás csuklós, így a rudak közötti szög akadálytalanul változhat. A rendszer a súlytalanság állapotában nyugalomban van, és a három golyó egy egyenes mentén helyezkedik el. Ekkor az \(\displaystyle A\) golyónak pillanatszerűen a rudakra merőleges, \(\displaystyle v_0\) nagyságú sebességet adunk. Mekkora erő hat a rudakban az indítást követő pillanatban?
Olimpiai versenyfeladat nyomán
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

