A KöMaL 2019. áprilisi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2019. május 10-én LEJÁRT. |
I. 481. (É). A minap képek kerültek elő egy 1980-as évekbeli lövöldözős számítógépes játékról. A programban a játékos a képernyő bal széléről elindított egy űrhajót, amelynek a megsemmisülést elkerülve kellett eljutnia a képernyő jobb szélére – ezért járt a pont. Az űrhajó útját ,,felülről'' hulló bombák akadályozták. Az első két találatot még túlélte, a harmadiknál viszont megsemmisült. Ha egy űrhajó utolért egy másik, nála lassabb űrhajót, akkor mindkettő megsemmisült.
Ebben a feladatban könnyebb dolgunk van, mint az egykori játékosoknak, pontosan ki tudjuk számítani a bombák becsapódási idejét és az elindított űrhajók útját.
A honlapunkról letölthető ur.txt fájlban megtaláljuk a bombák és az elindított űrhajók adatait. Az első sor két számot tartalmaz: az első a bombák \(\displaystyle B\), a második az űrhajók \(\displaystyle U\) száma. A következő \(\displaystyle B\) sorban soronként három egész szám és egy karakter, a bombák adatai szerepelnek: az első a bomba becsapódásának az űrhajó indítási helyétől mért távolsága, a következő az indítás magassága, a harmadik az indítás időpontja, a negyedik a bomba típusa, amely a becsapódáskor észlelt színhatással egyezik. Minden bomba egységnyi idő alatt egységnyi távolságot tesz meg. Az első három egész szám, az utolsó pedig egyetlen karakter. Tudjuk, hogy egy időpontban adott távolságban csak egy bomba robban. A következő \(\displaystyle U\) sorban soronként két egész szám, az űrhajók adatai láthatók. Az első szám az indítás időpontja, a második az űrhajó sebessége (a táv, amelyet egységnyi idő alatt megtesz, értéke 1 és 5 közötti). A fájlban a bombák adatai a távolság, azon belül az indítás magassága szerint rendezettek, az űrhajók pedig indítási sorrendben vannak.
1. Olvassuk be és tároljuk el az ur.txt fájl tartalmát.
2. Jelenítsük meg, hogy az indítás helyéhez legközelebbi és legtávolabbi olyan helyen, ahol indítottak bombát, összesen hány bombát indítottak.
3. Határozzuk meg, hogy hol robbant az első bomba.
4. Olvassunk be egy időpontot és határozzuk meg, hogy abban a pillanatban hol, milyen típusú bombák robbannak.
5. Határozzuk meg, hogy mely űrhajók semmisülnek meg az első 100 egységnyi távolságon belül egy másik űrhajóval való ütközés miatt.
6. Készítsük el az eredmeny.txt fájlt, amelybe űrhajónként jegyezzük meg, hogy mely helyeken milyen bombák találták el. Minden találathoz két szám tartozik, az első a távolság, a második a típus. Ha az űrhajó egy találatot sem kapott, a sor maradjon üresen. (Az űrhajók közötti ütközéseket ne vegyük figyelembe.)
7. Olvassunk be egy sebességadatot. Határozzuk meg, hogy mikor van az első olyan indítási időpont, amikor ezzel a beolvasott sebességgel haladva az űrhajó átjut a túloldalra. (Az űrhajók közötti ütközéseket most ne vegyük figyelembe.)
Letölthető állomány: ur.txt
Beküldendő egy i481.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
I. 482. A mérgezett csoki egy nagyon egyszerűen leírható kétszemélyes játék. A játékosok felváltva ,,harapnak'' a táblából és az veszít, aki kénytelen a mérgezett csokoládécikket ,,kiharapni''. Ismert, hogy a kezdőnek van nyerő stratégiája, de az csak az \(\displaystyle N\times N\) és a \(\displaystyle 2\times N\) méretű tábla esetén fogalmazható meg egyszerűen, más méretű táblát használva a játék valós izgalmat hordoz.
A játékról bővebben például a http://web.cs.elte.hu/szakdolg/ghorvath.pdf oldalon olvashatunk.
Ebben a feladatban a következő formában játszunk:
\(\displaystyle \bullet\) a csokoládé tábla \(\displaystyle N\) sorból és \(\displaystyle M\) oszlopból áll;
\(\displaystyle \bullet\) az egyes csokoládécikkeket két egész számmal azonosítjuk;
\(\displaystyle \bullet\) a mérgezett csokoládécikk az \(\displaystyle (M, N)\) helyen található;
\(\displaystyle \bullet\) a táblából minden lépésben legalább egy cikket ,,harapunk'' ki, a harapást a jobb felső sarokkal adjuk meg \(\displaystyle (i, j)\). Ekkor minden olyan még meglévő \(\displaystyle (x, y)\) csokoládécikket elveszünk, amelyre \(\displaystyle x\le i\) és \(\displaystyle y\le j\).
A játékot most táblázatkezelő program segítségével valósítsuk meg (a témával foglalkoztunk már az I. 466. feladatban) egy 10 oszlopból és 12 sorból álló tartományban. A táblát a munkafüzet Játék munkalapján jelenítsük meg a D1:M12 tartományban. A játékosok lépéseiket felváltva jegyzik be az A és B oszlopba az alábbi mintának megfelelően. A játékot kezdő játékos színe sárga, a másiké a zöld. Jelöljük sárga háttérrel a kezdő játékos lépéseinek sorait az A és a B oszlopban, valamint a játéktáblán az általa ,,kiharapott'' csokoládécikkeket. Ugyanezeket a másik játékos esetén zölddel valósítsuk meg. A még meglévő csokoládécikkek színe legyen barna. Ha valamelyik játékos szabálytalanul lép, azaz egyetlen cikket sem harap ki, a lépés sora legyen piros. Ha valaki a mérgezett cikket veszi el és így a játék befejeződik, a lépés sora legyen fekete háttérrel és fehér karakterekkel megjelenítve. A szabálytalan és a játékzáró lépést követő sorok háttér- és szövegszíne egyaránt fehér legyen. (A minta a jobb olvashatóság érdekében csak a tábla színezését mutatja.)

A szükséges segédszámításokat a Segéd munkalapon végezzük, amihez tetszőleges számú cellát használhatunk. A megoldáshoz csak beépített függvényeket alkalmazhatunk. A megoldás során törekedjünk másolható képletek használatára. (A felhasznált cellák és képletek száma a megoldás értékelését nem befolyásolja.)
Beküldendő egy i482.zip tömörített állományban a megoldást tartalmazó i482 munkafüzet és a dokumentációt magában foglaló i482.pdf fájl. A dokumentáció tartalmazza a használt táblázatkezelő nevét, verziószámát és a megoldás során használt képleteket és azok szerepének rövid leírását.
(10 pont)
I. 483. A címer általában pajzs alakú, szabályok szerint megszerkesztett jelvény, melyet egy intézmény vagy testület a saját maga azonosítására örökletesen, állandó jelleggel használ. A címertannal a heraldikusok foglalkoznak. Készítsük el iskolánk címerét egy SVG típusú képállományba vektorgrafikus rajzolóprogrammal. Ha az iskolai címer nem alkalmas alakzatokkal való elkészítésre, akkor helyette városi, kerületi címert is választhatunk. A rajzon használhatunk rasztergrafikus elemeket is, de minél több részletet magunk készítsünk el. A megoldáshoz ajánljuk az Inkscape (internetről ingyenesen letölthető és fölhasználható) vektorgrafikus rajzolóprogramot.
Értékelés: a pontok 80%-a kapható, ha a rajz csoportbontással összetevőkre bontható és további 20%, ha animáció mutatja be az összetevőkből a rajz összeállítását. Az animáción az alakzatok olyan sebességgel mozogjanak (forgás vagy eltolás), hogy a rajz kialakulása megfigyelhető legyen. Ilyen feladattal foglalkozott az I. 357. feladat.
Beküldendő a képállomány (i483.svg), valamint egy rövid leírás (i483.txt, i483.pdf, \(\displaystyle \ldots\)), amely tartalmazza az interneten elérhető eredeti címer hivatkozását.
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2019. május 10-én LEJÁRT. |
I/S. 35. Adott \(\displaystyle N\) darab téglalap a koordinátasíkon. A téglalapok oldalai párhuzamosak a tengelyekkel. Adjuk meg, hogy a téglalapok összesen mekkora területet fednek le.
Standard bemenet: az első sor tartalmazza az \(\displaystyle N\) számot. A következő \(\displaystyle N\) darab sor egy-egy téglalap bal fölső és jobb alsó alsó sarkának \(\displaystyle x\) és \(\displaystyle y\) koordinátáit tartalmazza. Kimenet: adjuk meg, hogy a téglalapok közösen mekkora területet fednek le.
Példa:
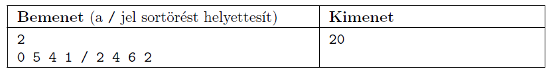
Korlátok: \(\displaystyle 1\le N\le 10\), \(\displaystyle -10\,000\le \text{koordináták}\le 10\,000\), egész értékek. Időlimit: 0,5 mp.
Beküldendő egy is35.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztő környezetben futtatható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2019. május 10-én LEJÁRT. |
S. 134. Szeretnénk új könyveket venni. Egy boltban \(\displaystyle N\) féle könyvet árusítanak, az \(\displaystyle i\)-ediket \(\displaystyle P_{i}\) forintért. Szerencsére rendelkezünk \(\displaystyle K\) darab kuponnal. Ha az \(\displaystyle i\)-edik könyv megvételekor elhasználunk egy kupont, akkor azt \(\displaystyle P_{i}\) helyett \(\displaystyle R_{i}\) forintért tudjuk megvásárolni. Egy könyvnél csak egy kupont tudunk elhasználni. Adjuk meg, hogy legföljebb hány könyvet tudunk megvásárolni \(\displaystyle M\) forintért.
A standard bemenet első sora tartalmazza az \(\displaystyle N\), \(\displaystyle K\), \(\displaystyle M\) számokat; a következő \(\displaystyle N\) darab sor tartalmazza a \(\displaystyle P_{i}\) és \(\displaystyle R_{i}\) számokat. A kimeneten adjuk meg, hogy legfeljebb hány könyvet tudunk megvenni.
Példa:
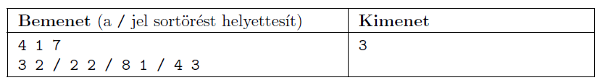
Korlátok: \(\displaystyle 1\le K\le N\le 50\,000\), \(\displaystyle 1\le M\le {10}^{14}\), \(\displaystyle 1\le R_{i}\le P_{i}\le {10}^{9}\). Időlimit: 0,5 mp.
Beküldendő egy s134.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztő környezetben futtatható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

