KöMaL Problems in Mathematics, September 2021
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on October 11, 2021. |
K. 694. How many seven-digit positive integers are there in which each digit is either \(\displaystyle 1\) or \(\displaystyle 2\) greater than the preceding digit? (Example: as in \(\displaystyle 1\,234\,678\).)
(5 pont)
solution (in Hungarian), statistics
K. 695. A point \(\displaystyle P\) is selected on side \(\displaystyle BC\) of a square sheet of paper \(\displaystyle ABCD\). The sheet is folded along the line \(\displaystyle AP\) so that point \(\displaystyle B\) should lie equidistant from vertices \(\displaystyle C\) and \(\displaystyle D\). The new position of point \(\displaystyle B\) is denoted by \(\displaystyle B'\). Determine the measure of angle \(\displaystyle CB'D\).
(5 pont)
solution (in Hungarian), statistics
K. 696. In the left front pocket of my jeans I have twice as much money as in the right front pocket, and one third as much as in the right back pocket. I moved 30 forints (HUF, Hungarian currency) from the right front pocket to the left front pocket, and also moved 180 forints from the right back pocket to the left front pocket. Now I have 3 times as much money in the left front pocket as the amount remaining in the right front pocket. How much money did I have initially in each pocket?
(5 pont)
 |
Problems with sign 'K/C'Deadline expired on October 11, 2021. |
K/C. 697. Some of the faces of a cube are coloured red, and then the cube is cut into small cubes of equal size. 45 of the small cubes have no painted faces. How many faces of the original cube were coloured?
(5 pont)
solution (in Hungarian), statistics
K/C. 698. Dorothy thought of an integer that is at least 3 and at most 25. Ann named a one-digit even number \(\displaystyle x\), and asked Dorothy whether her number is a perfect square, whether it is prime, and whether it is a multiple of \(\displaystyle x\). Dorothy said if she gave the answer to each of these questions, Ann would be able to figure out what number she had in mind. What is Dorothy's number?
(5 pont)
 |
Problems with sign 'C'Deadline expired on October 11, 2021. |
C. 1679. Prove that the value of the expression
\(\displaystyle 1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\ldots+\frac{1}{2021}-\frac{1}{2022} \)
is between \(\displaystyle 0\) and \(\displaystyle 1\).
(5 pont)
solution (in Hungarian), statistics
C. 1680. One side of a quadrilateral is 5 cm long, and the measures of the angles lying on it are \(\displaystyle 90^{\circ}\) and \(\displaystyle 60^{\circ}\). Given that the quadrilateral has both an inscribed circle and a circumscribed circle, find a method to construct the quadrilateral. Write down the steps of the construction. (Elementary steps of construction, like bisecting an angle or reflecting about a line do not need to be described in detail.)
Proposed by N. Zagyva, Baja
(5 pont)
solution (in Hungarian), statistics
C. 1681. Let \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) denote nonzero real numbers that add up to \(\displaystyle 0\). Prove that
\(\displaystyle \frac{a^3-a^2+b^3-b^2+c^3+c^2}{ab}=3c+2. \)
(5 pont)
solution (in Hungarian), statistics
C. 1682. The vertices of a unit cube are \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\), \(\displaystyle E\), \(\displaystyle F\), \(\displaystyle G\), \(\displaystyle H\) as shown in the figure. The tetrahedra \(\displaystyle ABDE\) and \(\displaystyle GCFH\) are cut off the cube. Find the volume and surface area of the remaining solid.
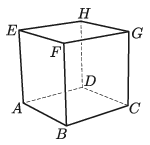
Proposed by N. Zagyva, Baja
(5 pont)
solution (in Hungarian), statistics
C. 1683. Ann and Bo are playing the following game on squared sheets of paper. Each player marks a \(\displaystyle 10\times10\) square on her own sheet of squared paper. In this large square, they colour seven \(\displaystyle 1\times1\) lattice squares blue, and another 14 lattice squares red. The players cannot see each other's coloured squares. The game starts by Ann naming a pair of numbers \(\displaystyle (i,j)\) where \(\displaystyle 1 \le i,j \le 10\) are positive integers. (For example, \(\displaystyle (5,2)\) means the lattice square at the intersection of row 5 and column 2 of the \(\displaystyle 10\times10\) square.) If the pair \(\displaystyle (i,j)\) determines a coloured field on Bo's sheet of paper then Bo will answer ``hit'', otherwise she will say ``no hit''. Then the game continues by switching roles: Bo names a pair of numbers and Ann answers. What is the probability that in the third round of the game Ann will hit a blue square and Bo will hit a red square provided that in the first two rounds neither Ann nor Bo had any hits?
(5 pont)
 |
Problems with sign 'B'Deadline expired on October 11, 2021. |
B. 5182. The number \(\displaystyle 612^2=374\,544\) ends in two digits of \(\displaystyle 4\) in base \(\displaystyle 10\) notation. What is the maximum number of digits of \(\displaystyle 4\) at the end of a perfect square?
Based on the idea of I. Blahota
(3 pont)
solution (in Hungarian), statistics
B. 5183. Side \(\displaystyle AB\) of a triangle \(\displaystyle ABC\) has unit length, \(\displaystyle \angle BAC = 60^{\circ}\), \(\displaystyle \angle ACB =100^{\circ}\) and the midpoint of side \(\displaystyle BC\) is \(\displaystyle F\). \(\displaystyle D\) is a point on side \(\displaystyle AB\) such that \(\displaystyle DB = FB\). Find the exact value of \(\displaystyle T_{ABC\triangle}+2T_{FBD\triangle}\), where \(\displaystyle T_{ABC\triangle}\) denotes the area of triangle \(\displaystyle ABC\). (\(\displaystyle T\) means the area of the triangle of the triangle named in the index.)
Proposed by S. Kiss, Nyíregyháza
(4 pont)
solution (in Hungarian), statistics
B. 5184. Cornelia marked four non-concyclic points in the plane. Then she drew all the circles that pass equidistant from the four points. What is the maximum possible number of circles she may have drawn? (The distance between point \(\displaystyle P\) and a circle \(\displaystyle k\) centred at \(\displaystyle O\) is defined as follows: let \(\displaystyle M\) denote the point where the ray starting at \(\displaystyle O\) and passing through \(\displaystyle P\) intersects the circle \(\displaystyle k\). Then the distance is the length of line segment \(\displaystyle PM\).)
(5 pont)
solution (in Hungarian), statistics
B. 5185. Find the real solutions of the equation
\(\displaystyle \sqrt[3]{4-x^2}+\sqrt{x^2-3}=1. \)
Proposed by M. Szalai, Szeged
(4 pont)
solution (in Hungarian), statistics
B. 5186. Al and Bill are playing the following game. They agree on a fixed number \(\displaystyle n \ge 3\), and then Al thinks of a number from the set \(\displaystyle \{1,2,\ldots,n \}\). Now Bill can guess the number. He will only get yes or no answers. If the answer is yes, the game terminates.
If the answer is no, Al will change the number: either increases or reduces it by 1, but the number must remain positive (it is allowed to go beyond \(\displaystyle n\) though). Then Bill can guess again, trying to hit the new number. The procedure is repeated until finally Bill gets the number.
Prove that Bill has a strategy to end the game with at most \(\displaystyle (3n-5)\) guesses.
Proposed by J. Szoldatics, Budapest
(6 pont)
solution (in Hungarian), statistics
B. 5187. A subset of the set \(\displaystyle S=\{1,2,\dots,n\}\) is called primitive, if it does not contain two elements such that one is a divisor of the other. Show that if it is not possible to add a further element of \(\displaystyle S\) to a particular primitive set \(\displaystyle A\subseteq S\) and keep it primitive, then either \(\displaystyle A=\{1\}\) or the size of \(\displaystyle A\) is greater than or equal to the number of primes up to \(\displaystyle n\).
Proposed by Cs. Sándor, Budapest
(6 pont)
solution (in Hungarian), statistics
B. 5188. Prove that the height of a circumscribed trapezium cannot be greater than the geometric mean of the bases.
Proposed by L. Németh, Fonyód
(5 pont)
solution (in Hungarian), statistics
B. 5189. The base edge of a right pyramid with a regular triangular base is \(\displaystyle a\). Let \(\displaystyle r\) be the radius of the inscribed sphere, and let \(\displaystyle R\) be the radius of the escribed sphere touching the base. Prove that \(\displaystyle a^2=12rR\).
Proposed by L. László, Budapest
(6 pont)
 |
Problems with sign 'A'Deadline expired on October 11, 2021. |
A. 803. Let \(\displaystyle \pi (n)\) denote the number of primes less than or equal to \(\displaystyle n\). A subset of \(\displaystyle S=\{1,2,\dots,n\}\) is called primitive if there are no two elements in it with one of them dividing the other. Prove that for \(\displaystyle n\ge 5\) and \(\displaystyle 1\le k<\frac{\pi (n)}{2}\) the number of primitive subsets of \(\displaystyle S\) with \(\displaystyle k+1\) elements is greater or equal to the number of primitive subsets of \(\displaystyle S\) with \(\displaystyle k\) elements.
Proposed by Cs. Sándor, Budapest
(7 pont)
A. 804. There is a city with \(\displaystyle n\) citizens. The city wants to buy sceptervirus tests with which it is possible to analyze the samples of several people at the same time. The result of a test can be the following:
\(\displaystyle \bullet\) Virus positive: there is at least one currently infected person among the people whose samples were analyzed, and none of them were healed from an earlier infection.
\(\displaystyle \bullet\) Antibody positive: there is at least one person who was healed from an earlier infection among the people whose samples were analyzed, and non of them are infected now.
\(\displaystyle \bullet\) Neutral: either all of the people whose samples were analyzed are not infected, or there is at least one currently infected person and one person who was healed from an earlier infection. (Viruses and antibodies in samples completely neutralize each other.)
What is the smallest number of tests to buy if we would like to know if the sceptervirus is present now or it has been present earlier? (The samples are taken from the people at the same time. The people are either infected now, have been infected earlier, or haven't contacted the virus yet.)
Submitted by Csongor Beke, Cambridge
(7 pont)
A. 805. In acute triangle \(\displaystyle ABC\) the feet of the altitudes are \(\displaystyle A_1\), \(\displaystyle B_1\) and \(\displaystyle C_1\) (with the usual notations on sides \(\displaystyle BC\), \(\displaystyle CA\) and \(\displaystyle AB\), respectively). The circumcircles of triangles \(\displaystyle AB_1C_1\) and \(\displaystyle BC_1A_1\) intersect the circumcircle of triangle \(\displaystyle ABC\) at points \(\displaystyle P\ne A\) and \(\displaystyle Q\ne B\), respectively. Prove that lines \(\displaystyle AQ\), \(\displaystyle BP\) and the Euler line of triangle \(\displaystyle ABC\) are either concurrent or parallel to each other.
Submitted by Géza Kós, Budapest
(7 pont)
Upload your solutions above.
