KöMaL Problems in Mathematics, December 2021
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on January 10, 2022. |
K. 709. A family are planning to grow a special type of onion in their garden. They want to eat 400 onion bulbs each year. The onion is grown from a seed. Each onion plant can produce 51 seeds every year if we let it. However, once an onion plant has gone into seeds, its bulb will dissolve during growing the seeds. What is the minimum number of seeds the family need to buy in order to launch the onion project so that they can have the desired quantity of onion bulbs to eat, and they never need to buy seeds any more?
(5 pont)
solution (in Hungarian), statistics
K. 710. There are some dodecahedra and some icosahedra on the table. The solids have 792 vertices and 936 faces altogether. How many dodecahedra and how many icosahedra are there on the table?
(5 pont)
solution (in Hungarian), statistics
K. 711. Ann's favourite number is 2468. Ben's favourite number also has four digits, and exactly two of its digits coincide with two digits of Ann's favourite number. Furthermore, each of the matching digits is in the same decimal place in both numbers. Based on this information, how many four-digit positive integers are there which may be Ben's favourite number?
(5 pont)
 |
Problems with sign 'K/C'Deadline expired on January 10, 2022. |
K/C. 712. We have 2022 square wooden plates arranged in a row, and 2021 discs numbered 1 to 2021. One disc is placed on each wooden plate except for the last one, in a random order. Then in each move, one disc is transferred to the (momentarily) vacant wooden square. Our goal is to have the numbers in increasing order, with the last square left vacant. What is the maximum number of moves that may be needed to achieve that goal? Also give an example for a possible initial arrangement that does require that maximum number of moves.
(5 pont)
solution (in Hungarian), statistics
K/C. 713. The sides of a square are 6 cm long. A circle is drawn over each side as diameter, as shown in the figure. The large circle is centred at the centre of the square and its radius equals the side of the square. Calculate the areas of the regions I., II. and III.
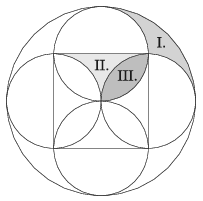
(5 pont)
 |
Problems with sign 'C'Deadline expired on January 10, 2022. |
C. 1694. Solve the following equation over the set of real numbers:
$$\begin{gather*} x-2021-\frac{x-2020}{2}+\frac{x-2019}{3}-\frac{x-2018}{4}+\frac{x-2017}{5}-\dots +{}\\ {} + \frac{x-3}{2019}-\frac{x-2}{2020}+\frac{x-1}{2021}-\frac{x}{2022}=0. \end{gather*}$$Proposed by L. Sáfár, Ráckeve
(5 pont)
solution (in Hungarian), statistics
C. 1695. A perpendicular line segment equal in length to the radius (\(\displaystyle R\)) is attached to the circumference of a circle (as shown in the figure). Is it possible to fit two such circles with handles (``frying pans'') in a rectangle if one side of the rectangle equals the diameter of the circle (\(\displaystyle 2R\)), and the other side is twice as long (\(\displaystyle 4R\))? The figures and the rectangle are allowed to touch one another but they are not allowed to intersect or overlap.
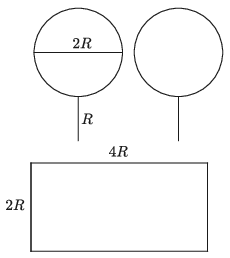
Proposed by M. E. Gáspár, Budapest
(5 pont)
solution (in Hungarian), statistics
C. 1696. There are \(\displaystyle 10\) and \(\displaystyle 15\) points marked on two parallel lines \(\displaystyle a\) and \(\displaystyle b\), respectively. Consider all line segments formed by the points marked such that one endpoint lies on \(\displaystyle a\), and the other lies on \(\displaystyle b\). How many intersections may these line segments have altogether at most?
(5 pont)
solution (in Hungarian), statistics
C. 1697. Interior points \(\displaystyle D\), \(\displaystyle E\), \(\displaystyle F\) are marked on sides \(\displaystyle BC\), \(\displaystyle CA\), \(\displaystyle AB\) of a regular triangle \(\displaystyle ABC\), respectively, such that \(\displaystyle DEF\) is also a regular triangle. Then regular triangles \(\displaystyle BDA'\) and \(\displaystyle AEB'\) are drawn over the sides \(\displaystyle BC\) and \(\displaystyle AC\), respectively, on the outside. Prove that there exists a point on side \(\displaystyle AB\) where each of the line segments \(\displaystyle A'E\) and \(\displaystyle B'D\) subtends a right angle.
(5 pont)
solution (in Hungarian), statistics
C. 1698. Zoe does not like books but she decides to read a total of 2021 pages during the year 2021. She is going to read on consecutive days, one page more on every day than on the previous day. How many pages should she read on the first day if she would like to spread the project through the largest possible number of days, but she does not have time to read more than 100 pages on any day?
Proposed by L. Sáfár, Ráckeve
(5 pont)
 |
Problems with sign 'B'Deadline expired on January 10, 2022. |
B. 5206. An \(\displaystyle n\)-digit number \(\displaystyle \overline{a_1a_2a_3\ldots a_n}\) is called hill type if there exists an integer \(\displaystyle 1 \le k \le n\) for which the sequence \(\displaystyle a_1,a_2,\ldots,a_k\) is strictly increasing and the sequence \(\displaystyle a_k,a_{k+1},\ldots,a_n\) is strictly decreasing. (For example, the numbers 1, 121, 1231 are of hill type, whereas 1442 or 12313 are not.) How many hill type numbers are there?
(3 pont)
solution (in Hungarian), statistics
B. 5207. Let \(\displaystyle n\ge 2\) be a natural number. Prove that there exist positive integers \(\displaystyle 2\le x_1<x_2<x_3< \dots<x_n\), such that
\(\displaystyle x_1!\cdot x_2!\cdot x_3!\cdot \dots \cdot x_n! \)
is a perfect square.
Proposed by J. Szoldatics, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 5208. The lines of two perpendicular chords \(\displaystyle AB\) and \(\displaystyle CD\) of a circle intersect at an exterior point \(\displaystyle P\). The length of the tangent drawn from \(\displaystyle P\) to the circle is \(\displaystyle e\). Show that the geometric mean of the lengths \(\displaystyle AD\) and \(\displaystyle BC\) is at least \(\displaystyle \sqrt2\,e\).
Proposed by Sz. Kocsis, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 5209. What is the maximum possible number of two-element subsets in a \(\displaystyle 2022\)-element set of integers for which the sum of the two elements also belongs to the set?
(5 pont)
solution (in Hungarian), statistics
B. 5210. The parabolas \(\displaystyle \mathcal{P}_1\), \(\displaystyle \mathcal{P}_2\) and \(\displaystyle \mathcal{P}_3\) have the same focus, and any two of them intersect at exactly two points. Let \(\displaystyle e_{ij}\) denote the line passing through the two intersections of the parabolas \(\displaystyle \mathcal{P}_i\) and \(\displaystyle \mathcal{P}_j\). Show that the lines \(\displaystyle e_{12}\), \(\displaystyle e_{13}\) and \(\displaystyle e_{23}\) are concurrent.
(5 pont)
solution (in Hungarian), statistics
B. 5211. Solve the following equation over the set of positive integers:
\(\displaystyle 5^x-2^y=1. \)
(5 pont)
solution (in Hungarian), statistics
B. 5212. Prove that there exists a positive integer which can be represented in at least 2021 different ways by taking an appropriate positive integer (in decimal notation), and adding the sum of its digits to it.
Proposed by Cs. Sándor, Budapest
(6 pont)
solution (in Hungarian), statistics
B. 5213. Prove that if \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) are positive real numbers, then
\(\displaystyle c\sqrt{a^2+b^2-ab}+a\sqrt{b^2+c^2-bc}\ge b\sqrt{c^2+a^2+ca}\,. \)
When will equality occur?
Proposed by J. Schultz, Szeged
(5 pont)
 |
Problems with sign 'A'Deadline expired on January 10, 2022. |
A. 812. Two players play the following game: there are two heaps of tokens, and they take turns to pick some tokens from them. The winner of the game is the player who takes away the last token. If the number of tokens in the two heaps are \(\displaystyle A\) and \(\displaystyle B\) at a given moment, the player whose turn it is can take away a number of tokens that is a multiple of \(\displaystyle A\) or a multiple of \(\displaystyle B\) from one of the heaps.
Find those pair of integers \(\displaystyle (k,n)\), for which the second player has a winning strategy, if the initial number of tokens is \(\displaystyle k\) in the first heap and \(\displaystyle n\) in the second heap.
Proposed by Dömötör Pálvölgyi, Budapest
(7 pont)
solution (in Hungarian), statistics
A. 813. Let \(\displaystyle p\) be a prime number and \(\displaystyle k\) a positive integer. Let
\(\displaystyle t=\sum_{j=0}^{\infty} \left\lfloor\frac{k}{p^j}\right\rfloor. \)
\(\displaystyle a)\) Let \(\displaystyle f(x)\) be a polynomial of degree \(\displaystyle k\) with integer coefficients such that its leading coefficient is 1 and its constant is divisible by \(\displaystyle p\). Prove that there exists \(\displaystyle n\in \mathbb{N}\) for which \(\displaystyle p\mid f(n)\), but \(\displaystyle p^{t+1}\nmid f(n)\).
\(\displaystyle b)\) Prove that the statement above is sharp, i.e. there exists polynomial \(\displaystyle g(x)\) of degree \(\displaystyle k\), integer coefficients, leading coefficient 1 and constant divisible by \(\displaystyle p\) such that if \(\displaystyle p\mid g(n)\) is true for a certain \(\displaystyle n\in \mathbb{N}\), then \(\displaystyle p^t\mid g(n)\) also holds.
Proposed by Kristóf Szabó, Budapest
(7 pont)
solution (in Hungarian), statistics
A. 814. There are given 666 points in the plane such that they cannot be covered with 10 lines. Prove that it is possible to choose 66 of them such that they still cannot be covered with 10 lines.
Proposed by Mihály Hujter, Budapest
(7 pont)
Upload your solutions above.
