KöMaL Problems in Mathematics, January 2022
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on February 10, 2022. |
K. 714. The first term of a sequence is 3, and every further term is obtained by subtracting 2 from the double of the previous term.
\(\displaystyle a)\) List the first 8 terms of the sequence.
\(\displaystyle b)\) Which of the numbers below occur as terms of the sequence, and which of them do not occur? If a number occurs as a term, find the index of the term, otherwise explain why it is not a term of the sequence.
\(\displaystyle 8194,\quad 649\,287\,365,\quad 29\,453\,759\,372,\quad 8\,398\,507\,839\,348. \)
(5 pont)
solution (in Hungarian), statistics
K. 715. We have two jugs. Each of them can hold 2 litres of liquid. Initially, one jug is filled with 2 litres of 100% orange juice, and the other contains 1 litre of water.
1. Half the orange juice is poured into the water jug, and stirred with a spoon. Then 1 litre of the mixture is poured back in the first jug.
2. The procedure is repeated once more: 1 litre is transferred from the first jug to the second, stirred, and 1 litre is transferred back to the first jug. Find the resulting percentage of orange juice in the content of each jug.
(5 pont)
solution (in Hungarian), statistics
K. 716. In a shop, three notebooks and two pens cost 1110 forints (HUF, Hungarian currency). Five notebooks and four pens cost 2010 forints. What is the price of one notebook, and what is the price of one pen?
(5 pont)
 |
Problems with sign 'K/C'Deadline expired on February 10, 2022. |
K/C. 717. In a regular dodecagon \(\displaystyle ABCDEFGHIJKL\) the squares \(\displaystyle ABPQ\) and \(\displaystyle GHRS\) are drawn on sides \(\displaystyle AB\) and \(\displaystyle GH\), on the inside, as shown in the figure. Show that \(\displaystyle PQ\) and \(\displaystyle RS\) are two opposite sides of a regular hexagon.
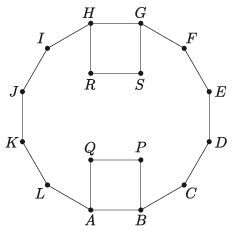
(5 pont)
solution (in Hungarian), statistics
K/C. 718. How many numbers are there from 1 to 50 that can be represented as a sum of at least two consecutive non-negative integers?
(5 pont)
 |
Problems with sign 'C'Deadline expired on February 10, 2022. |
C. 1699. In the expansion of the product \(\displaystyle (x+1)\cdot(x^2+1)\cdot(x^3+1)\cdot \ldots \cdot(x^{12}+1)\), what is the coefficient of the term in \(\displaystyle x^{14}\)?
(5 pont)
solution (in Hungarian), statistics
C. 1700. In a circle of centre \(\displaystyle O\), \(\displaystyle A\) is an interior point different from \(\displaystyle O\). For a point \(\displaystyle B\) on the circumference of the circle, \(\displaystyle \angle OAB =\alpha\). Let \(\displaystyle C\) be a point on the circumference such that \(\displaystyle 2\alpha+\beta=180^{\circ}\), where \(\displaystyle \angle BAC =\beta\), and the angles \(\displaystyle \angle BAO\) and \(\displaystyle \angle BAC\) have no common points apart from the ray \(\displaystyle AB\). Prove that the points \(\displaystyle O\), \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) are concyclic.
\
(5 pont)
solution (in Hungarian), statistics
C. 1701. What is the sum of all integers \(\displaystyle x\) for which
\(\displaystyle \sqrt{2x^2-6x-20}<-x+5? \)
(5 pont)
solution (in Hungarian), statistics
C. 1702. Vertex \(\displaystyle A\) of a quadrilateral \(\displaystyle ABCD\) lies on the plane \(\displaystyle S\), its diagonal \(\displaystyle BD\) is parallel to the plane \(\displaystyle S\), and its vertex \(\displaystyle C\) is at a distance of \(\displaystyle 8\) units from the plane \(\displaystyle S\). Given that the orthogonal projection of the quadrilateral onto \(\displaystyle S\) is a square with a diagonal \(\displaystyle 6\) units long, prove that quadrilateral \(\displaystyle ABCD\) is a rhombus, and calculate the length of its sides.
Proposed by N. Zagyva, Baja
(5 pont)
solution (in Hungarian), statistics
C. 1703. The natural numbers \(\displaystyle a\) and \(\displaystyle b\) each have only digits of \(\displaystyle 1\) in decimal notation. Prove that if \(\displaystyle a\) and \(\displaystyle b\) are not relatively prime then the sums of their digits, \(\displaystyle S(a)\) and \(\displaystyle S(b)\) are not relatively prime either.
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 10, 2022. |
B. 5214. The sequence of digits 110 represents an even integer, whatever positive integer greater than 1 is the base of notation. Is there a sequence of digits 1 and 0 such that it represents a multiple of 3, whatever positive integer greater than 1 is the base of notation?
(3 pont)
solution (in Hungarian), statistics
B. 5215. Find all positive real numbers \(\displaystyle x\) for which \(\displaystyle x + \frac1{x}\) is an integer, and \(\displaystyle x^3 + \frac1{x^3}\) is a prime number.
Based on the idea of B. and V. Szaszkó-Bogár
(4 pont)
solution (in Hungarian), statistics
B. 5216. The tangents drawn to the circumscribed circle of a right triangle \(\displaystyle ABC\) at the right-angled vertex \(\displaystyle C\) and at another vertex \(\displaystyle A\) intersect at \(\displaystyle D\). Prove that the line \(\displaystyle BD\) bisects the altitude drawn from vertex \(\displaystyle C\).
(3 pont)
solution (in Hungarian), statistics
B. 5217. A new triangle is constructed out of the line segments obtained by multiplying the medians of a triangle by \(\displaystyle \frac{2}{\sqrt3}\). The procedure is repeated with the triangle obtained. Show that the triangle obtained in the second step is congruent to the original triangle.
Proposed by P. Bártfai, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 5218. What is the largest number of elements that can be selected out of the first \(\displaystyle 2022\) positive integers such that the difference of any two selected numbers is not a prime?
(5 pont)
solution (in Hungarian), statistics
B. 5219. Prove that
\(\displaystyle \frac{|a+b+c|}{1+|a+b+c|}\le \frac{|a|}{1+|a|}+\frac{|b|}{1+|b|}+\frac{|c|}{1+|c|}. \)
for all real numbers \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\). On what condition will equality occur?
Proposed by J. Schultz, Szeged
(5 pont)
solution (in Hungarian), statistics
B. 5220. Let \(\displaystyle n\) be a positive integer. Prove that it is possible to select \(\displaystyle n\) perfect squares from the numbers \(\displaystyle 1\) to \(\displaystyle 2^{n+2}\) such that the sums obtained by adding an arbitrary subset of the selected numbers (including sums of single terms and the sum of all the numbers) are all distinct.
Proposed by R. Freud, Budapest
(6 pont)
solution (in Hungarian), statistics
B. 5221. In an acute-angled triangle \(\displaystyle ABC\), the points of tangency of the inscribed circle on sides \(\displaystyle BC\), \(\displaystyle CA\), \(\displaystyle AB\) are \(\displaystyle D\), \(\displaystyle E\), and \(\displaystyle F\), respectively. The circumscribed circle of the triangle intersects circle \(\displaystyle AEF\) at a point \(\displaystyle P\) different from \(\displaystyle A\), intersects circle \(\displaystyle BFD\) at a point \(\displaystyle Q\) different from \(\displaystyle B\), and intersects circle \(\displaystyle CDE\) at a point \(\displaystyle R\) different from \(\displaystyle C\). Show that the lines \(\displaystyle DP\), \(\displaystyle EQ\) and \(\displaystyle FR\) are concurrent.
Proposed by M. Lovas, Budapest
(6 pont)
 |
Problems with sign 'A'Deadline expired on February 10, 2022. |
A. 815. Let \(\displaystyle q\) be a monic polynomial with integer coefficients. Prove that there exists a constant \(\displaystyle C\) depending only on polynomial \(\displaystyle q\) such that for an arbitrary prime number \(\displaystyle p\) and an arbitrary positive integer \(\displaystyle N\le p\) the congruence \(\displaystyle n! \equiv q(n) \pmod{p}\) has at most \(\displaystyle CN^{2/3}\) solutions among any \(\displaystyle N\) consecutive integers.
Submitted by Navid Safaei, Iran
(7 pont)
solution (in Hungarian), statistics
A. 816. Peter has 2022 pieces of magnetic railroad cars, which are of two types: some has the front with north and the rear with south magnetic polarity, and some has the rear with north and the rear with south magnetic polarity (on these railroad cars the front and the rear can be distinguished). Peter wants to decide whether there are the same number of both type of cars. He can try to fit together two cars in one try. What is the least number of tries needed?
Submitted by Dömötör Pálvölgyi, Budapest
(7 pont)
solution (in Hungarian), statistics
A. 817. Let \(\displaystyle ABC\) be a triangle. Let \(\displaystyle T\) be the point of tangency of the circumcircle of triangle \(\displaystyle ABC\) and the \(\displaystyle A\)-mixtilinear incircle (the circle which is tangent to sides \(\displaystyle AB\), \(\displaystyle AC\), and internally tangent to the circumcircle of triangle \(\displaystyle ABC\)). The incircle of triangle \(\displaystyle ABC\) has center \(\displaystyle I\) and touches sides \(\displaystyle BC\), \(\displaystyle CA\) and \(\displaystyle AB\) at points \(\displaystyle D\), \(\displaystyle E\) and \(\displaystyle F\), respectively. Let \(\displaystyle N\) be the midpoint of line segment \(\displaystyle DF\). Prove that the circumcircle of triangle \(\displaystyle BTN\), line \(\displaystyle TI\) and the perpendicular from \(\displaystyle D\) to \(\displaystyle EF\) are concurrent.
Submitted by Diaconescu Tashi, Romania
(7 pont)
Upload your solutions above.
