KöMaL Problems in Physics, April 2022
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on May 16, 2022. |
M. 413. Measure the refractive index of cooking oil.
(6 pont)
 |
Problems with sign 'G'Deadline expired on May 16, 2022. |
G. 777. We would like to heat room temperature espresso coffee by ``steaming''. Estimate how much the ``quality'' of the coffee deteriorates, that is, how much the coffee concentration decreases.
(4 pont)
solution (in Hungarian), statistics
G. 778. The figure shows the wet track of a bicycle on a dry asphalt after the bicycle passed a puddle. Did the bike move from the left to the right or from the right to the left? Which trail was made by the front wheel and which one was made by the rear one?
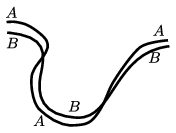
(3 pont)
solution (in Hungarian), statistics
G. 779. Would there be tides on the Moon if its surface was covered by oceans and landmasses?
(3 pont)
solution (in Hungarian), statistics
G. 780. Are fish disturbed by fishermen talking 2 metres away from the shore? (The speed of sound is 340 m/s in air and 1500 m/s in water.)
(4 pont)
 |
Problems with sign 'P'Deadline expired on May 16, 2022. |
P. 5400. One of the little prince's spherical planets is spinning so fast that the gravitational acceleration on its equator is zero. In which direction do the trees on the planet grow?
(4 pont)
solution (in Hungarian), statistics
P. 5401. A small (considered point-like) but heavy body is held by two ropes having the same length and approximately the same working load limit. The upper ends of the ropes are slowly moved apart along a horizontal line. When the angle between the ropes becomes \(\displaystyle 2\alpha\), one of the ropes breaks and the body begins to swing as a pendulum about the fixed end of the other rope. What could the value of \(\displaystyle \alpha\) be if the other rope does not break during the motion?
(5 pont)
solution (in Hungarian), statistics
P. 5402. A point-like weight \(\displaystyle m\) is attached to a thin ring of radius \(\displaystyle R\) and of negligible mass The ring moves out of its unstable equilibrium position shown in the figure, and it starts slipping on the ground when the displacement of its centre is just \(\displaystyle R\). What is the coefficient of friction between the ring and the horizontal ground?
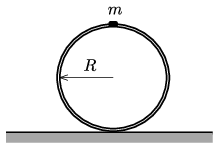
(5 pont)
solution (in Hungarian), statistics
P. 5403. Someone suggested building a mobile dam from iron sheets: a horizontal one and another which is attached to it and is tilted at an angle of \(\displaystyle 45^\circ\). The length of the edges of the sheets which are perpendicular to the common intersection line of the two sheets are 1 metre and \(\displaystyle \sqrt2\) metres, and the width of the iron sheets is 2 cm. ``This structure is pressed against the ground not only by the weight of the iron plates but also by the pressure of the water'' – argued the inventor.
\(\displaystyle a)\) What is the least value of the coefficient of static friction between the mobile dam and the ground in order that the dam should be able to protect safely even if the water level is maximum (that is: the level of the water reaches the top edge of the slant iron sheet)?
\(\displaystyle b)\) Where is the point of application of the vertical normal force exerted by the ground on the mobile barrier of this shape, if we use iron sheets having a thickness less than 2 cm or more than 2 cm? Can the mobile dam overturn in the case of the highest water level (i.e. when the water just to the top of the tilted iron plate)?
Investigate the two options for installing the mobile dam:
\(\displaystyle (i)\) the tilted surface slopes towards the water;
\(\displaystyle (ii)\) the tilted surface slopes towards the area to be protected (see the figure).
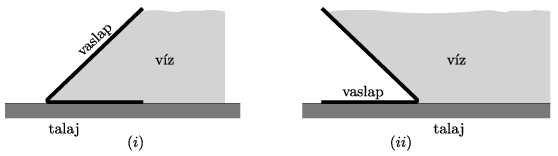
(5 pont)
solution (in Hungarian), statistics
P. 5404. An ideal Carnot heat engine, with the help of heat reservoirs of temperatures \(\displaystyle T_1\) and \(\displaystyle T_2\) \(\displaystyle (T_2<T_1)\), can perform \(\displaystyle W\) work in each cycle (through isothermal and adiabatic processes). How will the efficiency of the heat engine change if the small friction between the piston in the working cylinder causes that \(\displaystyle 2q\) heat in each cycle is released (\(\displaystyle q\ll W)\), and this heat is absorbed evenly by the two heat reservoirs?
(5 pont)
solution (in Hungarian), statistics
P. 5405. The sum of the currents through two resistors is \(\displaystyle I\). Prove that the total dissipated power in the two resistors is minimum if the voltages across the two resistors are equal.
(4 pont)
solution (in Hungarian), statistics
P. 5406. What is the maximum potential difference that can be created with the help of two alike capacitors and a battery of electromotive force \(\displaystyle U\)? The capacitors can be rearranged and connected into a circuit again after they were charged.
(5 pont)
solution (in Hungarian), statistics
P. 5407. Protons initially considered stationary in a linear accelerator at CERN are accelerated along a path of \(\displaystyle L=30.0\) m through a voltage of \(\displaystyle U=500\) MV. The electric field in the accelerator can be considered uniform. How long does it take for the protons to travel the distance \(\displaystyle L\)?
(5 pont)
solution (in Hungarian), statistics
P. 5408. A simple pendulum is attached to the top of a rod mounted to a trolley of mass \(\displaystyle M=3m\). The trolley is on a horizontal surface. The length of the thread of the pendulum is \(\displaystyle L=50\) cm, and the mass of the point-like bob at its end is \(\displaystyle m=0.15\) kg. Initially the objects are at rest. Then the pendulum bob is displaced such that its thread is tight and horizontal, and then released without initial speed. Friction is negligible everywhere.
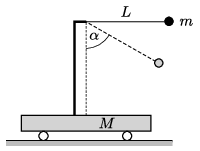
\(\displaystyle a)\) What is the speed of the trolley, when the angle between the thread and the vertical is \(\displaystyle \alpha = 60^\circ\)?
\(\displaystyle b)\) What is the tension in the thread at this position?
(6 pont)
Upload your solutions above.
