KöMaL Problems in Mathematics, April 2022
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'C'Deadline expired on May 10, 2022. |
C. 1714. The integers 1 to 22 are written on a blackboard. In each move, a pair of numbers is selected, erased and replaced with the absolute value of their difference. Prove that the last number added to the board is odd.
(German problem)
(5 pont)
solution (in Hungarian), statistics
C. 1715. A circle \(\displaystyle k_1\) of radius 8 cm lies in the interior of a circle \(\displaystyle k\). Both circles intersect the circle \(\displaystyle k_2\) of radius 15 cm, as shown in the figure. What is the radius of \(\displaystyle k\) if the shaded area inside \(\displaystyle k\) but outside \(\displaystyle k_1\) is equal to the total area of the shaded regions in the interior of \(\displaystyle k_2\)?
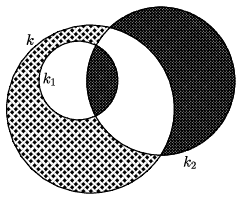
(5 pont)
solution (in Hungarian), statistics
C. 1716. In factorial representation, the place values of the digits are not the powers of a base: the \(\displaystyle n\)th place value is \(\displaystyle n\) factorial. Thus the digit in the first place is to be multiplied by 1, the digit in the second place is multiplied by 2, that in the third place is multiplied by 6, and so on. For example, the number \(\displaystyle 3310_!\) in factorial representation corresponds to the number \(\displaystyle 3\cdot4!+3\cdot3!+1\cdot2!=92\) in decimal notation. (If there is a number of more than one decimal digits in a certain place then it is indicated by using brackets.) (It can be shown that the representation is unique, that is, every positive integer has a single factorial representation. See the Informatics problems I. 553. of the January issue.) It is observed that one third of \(\displaystyle 111_!\) is \(\displaystyle 11_!\), one third of \(\displaystyle 111\;111_!\) is \(\displaystyle 22\;011_!\), and one third of \(\displaystyle 111\;111\;111_!\) is \(\displaystyle 33\;022\;011_!\). Determine the factorial representation of one third of the number that consists of \(\displaystyle 3n\) digits of 1, also given in factorial representation.
Based on the idea of I. Lénárt, Budapest
(5 pont)
solution (in Hungarian), statistics
C. 1717. Let \(\displaystyle x_1\) and \(\displaystyle x_2\) denote the two real roots of the equation \(\displaystyle 15x^2-21x+7=0\). Find the exact value of the expression
\(\displaystyle \frac{x_1}{x_2}+\frac{x_2}{x_1}+\frac{1}{x_1}+\frac{1}{x_2} \)
(5 pont)
solution (in Hungarian), statistics
C. 1718. Eight unit cubes are placed on a plane, and five further unit cubes are placed on top of them as shown in the figure.
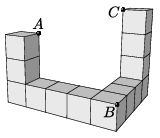
Find the lengths of the sides of triangle \(\displaystyle ABC\).
(5 pont)
solution (in Hungarian), statistics
C. 1719. In the interior of a regular triangle \(\displaystyle ABC\) consider the points \(\displaystyle P\) where side \(\displaystyle AB\) subtends an angle of \(\displaystyle 135^{\circ}\). Prove that the line segments \(\displaystyle PA\), \(\displaystyle PB\), \(\displaystyle PC\) can always form a triangle, and one angle of such triangles is always the same, independently of the position of point \(\displaystyle P\).
(5 pont)
solution (in Hungarian), statistics
C. 1720. The elements of a given set of \(\displaystyle 10\) elements are all at most two-digit positive integers. Is it true that such a set will always have two disjoint subsets in which the sum of the elements is equal?
(5 pont)
 |
Problems with sign 'B'Deadline expired on May 10, 2022. |
B. 5238. Solve the following equation over the set of positive integers:
\(\displaystyle (k+n)!=k^3+n^3+(k+n)(3kn-1). \)
Proposed by M. Szalai, Szeged
(3 pont)
solution (in Hungarian), statistics
B. 5239. The sides \(\displaystyle a\), \(\displaystyle b\) and \(\displaystyle c\) of a triangle, in this order, form an arithmetic sequence. Show that the centre of the inscribed circle divides the angle bisector drawn to side \(\displaystyle b\) in a \(\displaystyle 1:2\) ratio.
(3 pont)
solution (in Hungarian), statistics
B. 5240. Show that every positive integer \(\displaystyle n\) has a multiple in which the sum of the digits is \(\displaystyle n\).
Proposed by Cs. Sándor, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 5241. In a triangle \(\displaystyle ABC\), the centre of the circumscribed circle is \(\displaystyle O\), and \(\displaystyle \angle ABC > 90^\circ\). The tangent drawn to the circumscribed circle at \(\displaystyle C\) intersects line \(\displaystyle AB\) at point \(\displaystyle P\), and the perpendicular drawn from \(\displaystyle P\) to \(\displaystyle BC\) intersects line \(\displaystyle OC\) at \(\displaystyle Q\). Prove that \(\displaystyle AB\) is perpendicular to \(\displaystyle AQ\).
Proposed by Z.\(\displaystyle \,\)L. Nagy, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 5242. Let \(\displaystyle m\) and \(\displaystyle n\) denote arbitrary positive integers. Consider those lattice points \(\displaystyle (x;y)\) in the Cartesian coordinate plane for which \(\displaystyle 1\le x\le m\) and \(\displaystyle 1\le y\le n\). What is the maximum possible number of points that can be selected out of these \(\displaystyle mn\) lattice points such that no four points selected should form a non-degenerate parallelogram?
Proposed by E. Füredi, Budapest
(6 pont)
solution (in Hungarian), statistics
B. 5243. In a triangle \(\displaystyle ABC\), \(\displaystyle \angle CAB =48^{\circ}\) and \(\displaystyle \angle ABC =54^{\circ}\). \(\displaystyle D\) is an interior point of the triangle such that \(\displaystyle \angle CDB =132^{\circ}\) and \(\displaystyle \angle BCD =30^{\circ}\). Prove that the line segments forming the polygon \(\displaystyle ACDB\) cannot form a triangle.
(5 pont)
solution (in Hungarian), statistics
B. 5244. Determine all integers \(\displaystyle n > 4\) such that \(\displaystyle (k,n) > 1\) for all composite numbers \(\displaystyle k\) less than \(\displaystyle n\).
Proposed by S. Róka, Nyíregyháza
(5 pont)
solution (in Hungarian), statistics
B. 5245. \(\displaystyle a)\) Prove that there exist infinitely many, pairwise non-similar triangles in which the lengths of the sides are integers, and one angle is 3 times as large as another.
\(\displaystyle b)\) Is there a triangle with the above property in which the lengths of the sides are all at most 10?
Based on the idea of M. Hujter, Budapest
(6 pont)
 |
Problems with sign 'A'Deadline expired on May 10, 2022. |
A. 824. An infinite set \(\displaystyle S\) of positive numbers is called thick, if in every interval of the form \(\displaystyle \big[1/(n+1), 1/n\big]\) (where \(\displaystyle n\) is an arbitrary positive integer) there is a number which is the difference of two elements from \(\displaystyle S\). Does there exist a thick set such that the sum of its elements is finite?
Proposed by Gábor Szűcs, Szikszó
(7 pont)
A. 825. Find all functions \(\displaystyle f\colon \mathbb{Z}^+\to \mathbb{R}^+\) that satisfy \(\displaystyle f(nk^2)=f(n)f^2(k)\) for all positive integers \(\displaystyle n\) and \(\displaystyle k\), furthermore \(\displaystyle \lim\limits_{n\to \infty} \frac{f(n+1)}{f(n)}=1\).
(7 pont)
solution (in Hungarian), statistics
A. 826. An antelope is a chess piece which moves similarly to the knight: two cells \(\displaystyle (x_1, y_1)\) and \(\displaystyle (x_2, y_2)\) are joined by an antelope move if and only if
\(\displaystyle \big\{|x_1-x_2|, |y_1-y_2|\big\} = \{3, 4\}. \)
The numbers from \(\displaystyle 1\) to \(\displaystyle 10^{12}\) are placed in the cells of a \(\displaystyle 10^6 \times 10^6\) grid. Let \(\displaystyle D\) be the set of all absolute differences of the form \(\displaystyle |a-b|\), where \(\displaystyle a\) and \(\displaystyle b\) are joined by an antelope move in the arrangement. How many arrangements are there such that \(\displaystyle D\) contains exactly four elements?
Proposed by Nikolai Beluhov, Bulgaria
(7 pont)
Upload your solutions above.
