Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány

Már regisztráltál?
Új vendég vagy?

A KöMaL 2005. decemberi matematika feladatai

Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.

Feladat típusok elrejtése/megmutatása:

K-jelű feladatok

A beküldési határidő 2006. január 10-én LEJÁRT.

K. 61. Egy Loire menti kastély 20×10 méteres téglalap alakú parkjában egy 1 méter széles szögletes ,,spirálút'' vezet a kert belsejébe. A kastély ura minden reggel végigsétál a csigavonalú sétányon (az út közepén halad, és mindig derékszögben fordul) a csigavonal legvégéig, ott meglocsolja az 1×1 méteres virágágyban levő fehér margarétáit, majd visszasétál. Mekkora utat tesz meg ezalatt?

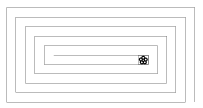
(6 pont)

megoldás, statisztika

K. 62. Zsófi logikai játékában 9 db, egy négyzet alakú falapba illesztett, különböző színű farúdra kell kilenc piros, kilenc zöld és kilenc kék, alakra egyforma fakarikát felhelyezni. (A rudak elrendezése felülnézetben látható az ábrán.) Helyes elrendezés akkor keletkezik, ha minden rúdon három különböző színű karika van, valamint ha mindhárom szinten az ábrán nyíllal jelölt irányokban három különböző színű karikát találunk. Hányféle helyes elrendezése létezik a karikáknak? (Két elrendezés akkor számít különbözőnek, ha legalább az egyik rúdon a két elrendezésben a karikák más sorrendben követik egymást.)

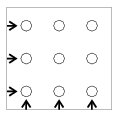
(6 pont)

megoldás, statisztika

K. 63. Az háromszögben X az AB, Y az AC oldal felezőpontja; BY és CX metszéspontja S. Mutassuk meg, hogy:

a) az SBX és az SCY háromszögek területe egyenlő;

b) az SBC háromszög és az AXSY négyszög területe egyenlő.

(6 pont)

megoldás, statisztika

K. 64. Adjuk meg két egész szám hányadosaként az alábbi összeget:

$\frac{4}{1989\cdot 1993}+\frac{4}{1993\cdot 1997}+\frac{4}{1997\cdot 2001}+\frac{4}{2001\cdot 2005}$

(6 pont)

megoldás, statisztika

K. 65. A valós x számra $x+\frac{1}{x}=5$ . Határozzuk meg az $x^2+\frac{1}{x^2}$ és az $x^3+\frac{1}{x^3}$ pontos értékét.

(6 pont)

megoldás, statisztika

K. 66. A karácsonyfán már csak 5 szem szaloncukor van: két zselés és három marcipános, de az ízük a csomagoláson nem látszik. Hanga elhatározta, hogy minden nap meg fog enni egyet közülük. Mi a valószínűbb: hogy a harmadik napon eszi meg a második zseléset, vagy hogy a negyedik napon a harmadik marcipánosat?

(6 pont)

megoldás, statisztika

C-jelű feladatok

A beküldési határidő 2006. január 16-án LEJÁRT.

C. 830. Lord Moneybag így szólt az unokájához: ,,Bill, figyelj jól! Mindjárt itt a karácsony. Magamhoz vettem egy 300 és 500 font közötti összeget, mégpedig 6 font egész számú többszörösét. Kapsz belőle 5 fontot 1 fontosokban. Amikor egy-egy fontot átadok neked, a nálam maradt összeg először osztható lesz 5-tel, majd 4-gyel, azután 3-mal, majd 2-vel, végül csak 1-gyel és önmagával. Ha megmondod, hány font van nálam, még egy tízes üti a markodat.'' Mennyi pénzt vett magához a lord?

(5 pont)

megoldás, statisztika

C. 831. Mennyi azoknak a háromjegyű számoknak az összege, amelyeknek minden számjegye páratlan?

(5 pont)

megoldás, statisztika

C. 832. Adott a koordinátarendszerben három pont: A(2;1), B(3;4), C(2;11). Igazoljuk, hogy az OB félegyenes felezi az AOC szöget.

(5 pont)

megoldás, statisztika

C. 833. Egy négyzet alapú egyenes gúla alapéle és magassága is 40 cm. Az oldallapokon szeretnénk egy vonalat rajzolni az alaplap egyik csúcsából az alaplap átellenes csúcsába. Milyen hosszú a legrövidebb ilyen vonal?

(5 pont)

megoldás, statisztika

C. 834. Oldjuk meg a következő egyenletet:

$\frac{1}{\sin x}-\frac{1}{\sin2x}=\frac{2}{\sin4x}.$

(5 pont)

megoldás, statisztika

B-jelű feladatok

A beküldési határidő 2006. január 16-án LEJÁRT.

B. 3862. Hányféleképpen lehet elhelyezni a 8×8-as sakktáblán 32 huszárt úgy, hogy semelyik kettő ne támadja egymást?

(4 pont)

megoldás, statisztika

B. 3863. Mutassuk meg, hogy az

$1^{2006}-2^{2006}+3^{2006}-4^{2006}+\ldots-2004^{2006}+2005^{2006}$

szám osztható 1003-mal. Osztható-e 2006-tal is?

(3 pont)

megoldás, statisztika

B. 3864. Az ABCD húrnégyszögben AC=BC. A C pont merőleges vetülete az AD és BD egyenesekre E, illetve F. Mutassuk meg, hogy AE=BF.

(3 pont)

megoldás, statisztika

B. 3865. Az AB₁C₁ és AB₂C₂ háromszögek hasonlók és a körüljárási irányuk is megegyezik. A B₁B₂ és C₁C₂ egyenesek az A-tól különböző D pontban metszik egymást.

(a) Mutassuk meg, hogy az AB₁B₂ és AC₁C₂ háromszögek hasonlók.

(b) Igazoljuk, hogy az AB₁C₁ és AB₂C₂ háromszög körülírt köre átmegy a D ponton.

(4 pont)

megoldás, statisztika

B. 3866. Egy kör AB ívének melyik P pontjára maximális az ABP háromszög kerülete?

(4 pont)

megoldás, statisztika

B. 3867. Legyen az n olyan pozitív egész szám, amelyre 4ⁿ+2ⁿ+1 prímszám. Bizonyítsuk be, hogy n a 3-nak egész kitevőjű hatványa.

(5 pont)

megoldás, statisztika

B. 3868. Ismeretes, hogy cos 2x előáll cos x polinomjaként:

cos 2x=2cos²x-1.

Előállítható-e sin 2x a sin x polinomjaként?

(4 pont)

megoldás, statisztika

B. 3869. Az ABC hegyesszögű háromszög belsejében, az A csúcsból induló szögfelezőn felvettük az M pontot. Az AM, BM, CM egyeneseknek a körülírt körrel való második metszéspontja rendre A₁, B₁ és C₁. Az AB és a C₁A₁ egyenesek az L pontban, az AC és a B₁A₁ egyenesek az N pontban metszik egymást. Bizonyítsuk be, hogy az LN szakasz párhuzamos BC-vel.

Javasolta: Bodnár János, Budapest

(5 pont)

megoldás, statisztika

B. 3870. Az F₁ és F₂ fókuszú ellipszisnek P a nagytengely végpontjaitól különböző pontja. Mutassuk meg, hogy

$\mathop{\rm tg} \frac{PF_1F_2\sphericalangle}{2}\cdot \mathop{\rm tg} \frac{PF_2F_1\sphericalangle}{2}$

értéke nem függ P-től.

(4 pont)

megoldás, statisztika

B. 3871. Oldjuk meg az x²-x-1=2^x-log₂(x²+2^x) egyenletet a pozitív számok körében.

(5 pont)

megoldás, statisztika

A-jelű feladatok

A beküldési határidő 2006. január 16-án LEJÁRT.

A. 386. Egy O középpontú derékszögű hiperbolának rajzoljuk meg az egyik ágát, és azon válasszunk ki egy tetszőleges P pontot. A P középpontú, 2OP sugarú kör messe a hiperbolaágat a Q és R pontokban. Igazoljuk, hogy $QPR\sphericalangle=120^\circ$ .

(5 pont)

megoldás, statisztika

A. 387. Van n látszólag egyforma golyónk, ami közül tudjuk, hogy az egyik radioaktív; ezt a golyót szeretnénk megtalálni. Egy radioaktivitást jelző műszer segítségével a golyók egy tetszőleges részhalmazáról el tudjuk dönteni, hogy a radioaktív golyó köztük van-e.

Olyan mérési stratégiát szeretnénk választani, amelyre a szükséges mérések számának várható értéke a lehető legkisebb. Határozzuk meg ezt a legkisebb lehetséges várható értéket.

(5 pont)

megoldás, statisztika

A. 388. Az ABCDEF hatszögben AB=BC, CD=DE és EF=FA. Bizonyítsuk be, hogy

$\frac{AB}{BE}+\frac{CD}{DA}+\frac{EF}{FC}\ge\frac32.$

(5 pont)

megoldás, statisztika

A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:

megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.

(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)