A KöMaL 2013. szeptemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2013. október 10-én LEJÁRT. |
M. 334. Vegyünk egy csupa egyforma szemből álló láncot, és helyezzük el az asztalon úgy, hogy egy része lelógjon az asztal szélén. Mikor kezd el lecsúszni az egész lánc az asztalról? Ennek alapján adjunk becslést a lánc és az asztal közötti tapadási súrlódási együttható nagyságára! Becslésünket ellenőrizzük más mérési módszerrel is!
Károly Ireneusz verseny, Esztergom
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2013. október 10-én LEJÁRT. |
P. 4551. Vízszintes helyzetű, mindkét végén zárt, 1 méter hosszú cső közepén elhanyagolható tömegű, súrlódásmentesen mozgó dugattyú van. A bal oldali rész oxigéngázt, a jobb oldali rész negyedannyi tömegű és azonos hőmérsékletű hidrogéngázt tartalmaz. Hol van a dugattyú egyensúlyi helyzete?
Hatvani István fizikaverseny, Debrecen
(3 pont)
P. 4552. Egy csónakban ülő horgász a tóba ejti a pipáját. Az így létrejövő vízszintváltozás nagysága ugyanakkora, mint amikor a pipát a partról ejti a tóba. Mekkora a pipa sűrűsége?
Öveges József emlékverseny, Tata
(4 pont)
P. 4553. Egy hőlégballon működését szeretnénk modellezni egy kis mécses és egy könnyű műanyagzsák felhasználásával. Adjunk becslést a felemelkedő zsák minimális térfogatára egy 20 oC-os szobában, ha a zsákban a levegő átlagos hőmérséklete 80 oC, a mécses, a zsák és a szerelvények tömege pedig összesen 12 gramm.
Lánczos Kornél fizikaverseny, Székesfehérvár
(4 pont)
P. 4554. Két asztal áll szorosan egymás mellett. Mennyi munkát végez az a személy, aki az egyik asztalon levő lapos csomagot a másikra áthúzza? A csomag és az asztallapok közötti súrlódási együtthatók különbözőek.
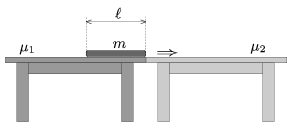
Adatok: m=18 kg; 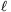 =0,8 m;
=0,8 m; 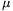 1=0,1;
1=0,1; 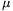 2=0,4. (A csomag súlya egyenletesen oszlik el az asztalokkal érintkező felületek mentén.)
2=0,4. (A csomag súlya egyenletesen oszlik el az asztalokkal érintkező felületek mentén.)
Jedlik Ányos fizikaverseny, Nyíregyháza
(4 pont)
P. 4555. Egy 4 méter hosszú, 1,2 kg tömegű lánc kicsire összetekerve nyugszik a 2 méter mély tó fenekén. Legalább mekkora mechanikai munkavégzés árán sikerül egyik végénél fogva, függőlegesen mozgatva, teljesen kihúzni a láncot a vízből? A lánc anyagának sűrűsége 3000 kg/m3.
Vermes Miklós fizikaverseny, Sopron
(4 pont)
P. 4556. Egy m1=2 kg és egy m2=3 kg tömegű, könnyen gördülő kiskocsi között D=240 N/m direkciós erejű csavarrugót vékony fonál tart megfeszítve. A rugó összenyomódása 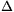
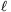 =15 cm. A két kocsi v=2 m/s sebességgel halad. Mekkora sebességgel haladnak a kocsik a fonál elszakadása után?
=15 cm. A két kocsi v=2 m/s sebességgel halad. Mekkora sebességgel haladnak a kocsik a fonál elszakadása után?
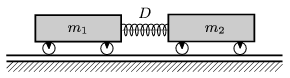
Mikola Sándor fizikaverseny, Gyöngyös
(4 pont)
P. 4557. Az ábrán látható rugó végére egy 0,6 kg tömegű vashenger van kötve, a vashenger aljára pedig egy 0,2 kg tömegű, korong alakú mágnes tapad. A 64 N/m direkciós erejű rugó kezdetben nyújtatlan, majd ebből a helyzetből a rendszert magára hagyjuk. A rezgés során a mágnes nem esik le a vashengerről.
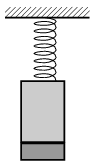
a) Mekkora a rezgés periódusideje?
b) Mekkora a mágnes legnagyobb sebessége?
c) Legalább mekkora a mágnes és a vashenger közötti vonzóerő?
Wigner Jenő fizikaverseny, Békéscsaba
(4 pont)
P. 4558. Egy dugattyúval ellátott edényben víz és annak telített gőze van 370 oC hőmérsékleten. A víz és a gőz együttes tömege 2 kg. Kezdetben a víz és a gőz együttes térfogata 8 dm3.
a) Mennyi ebből a gőz térfogata?
b) A dugattyút beljebb tolva - a hőmérsékletet állandó értéken tartva - a térfogatot 5 dm3-re csökkentjük. Mennyi lesz az új gőztérfogat?
c) Hány molekulával van most kevesebb a gőztérben, mint korábban?
Bay Zoltán fizikaverseny, Békéscsaba
(4 pont)
P. 4559. Az 5 cm3 normál állapotú levegőt tartalmazó töltőtoll-dozimétert, amelynek kapacitása 1 pF, töltsük fel 1000 V-ra. Mennyi az elnyelt dózis, ha a besugárzás után a feszültség 900 V-ra csökken? A levegő átlagos ionizációs energiája 6,88 aJ, sűrűségét vegyük 1,3 kg/m3-nek.
Szilárd Leó nukleáris verseny, Paks
(4 pont)
P. 4560. Gyapjas mamut csontokat találtak Észak-Amerikában. A legfiatalabb csontok C-14 aktivitása egy ma élő állat csontjaiban lévő aktivitás 21%-a. Hány évvel ezelőtt tűntek el a gyapjas mamutok Észak-Amerikából?
Tornyai Sándor fizikaverseny, Hódmezővásárhely
(4 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

