Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány

Már regisztráltál?
Új vendég vagy?

A KöMaL 2013. decemberi matematika feladatai

Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.

Feladat típusok elrejtése/megmutatása:

K-jelű feladatok

A beküldési határidő 2014. január 10-én LEJÁRT.

K. 397. Egy sziget önálló országként működik, pénzneme a fabatka. Mindenki minden megszerzett jövedelme után (függetlenül az elért jövedelem nagyságától) annak egy bizonyos százalékát be kell fizesse adóként az államkasszába. Azonban a kormányzat támogatni szeretné a gyerekek felnevelését, ezért minden családnak a megszerzett jövedelem utáni adóból az általuk nevelt gyerek után gyerekenként adott összegű adókedvezményt biztosít (pl. két gyerek után így kétszer annyi fabatka adókedvezmény jár, mint egy gyerek után). Egy család összes jövedelme egy évben 1500000 fabatka, egy gyerekük van, és a befizetendő adójuk nagysága 150000 fabatka. Egy másik család összes jövedelme egy évben 2500000 fabatka, két gyerekük van, és a befizetendő adójuk 225000 fabatka. A jövedelem hány százalékát kell befizetni adóként, és mennyi az egy gyerek után járó adókedvezmény nagysága?

(6 pont)

megoldás, statisztika

K. 398. A 135726 egy olyan hatjegyű szám, amelyben az ezresek helyén álló számjegy (az 5-ös) egyenlő a százezresek duplájának és a tízezreseknek az összegével (azaz 2^.1+3-mal). A százasok helyén álló számjegy (a 7-es) egyenlő a tízezresek duplájának és a százezreseknek az összegével (azaz 2^.3+1-gyel). A tízes helyiértéken lévő számjegy a százezresek, az egyes helyiértéken lévő számjegy pedig a tízezresek kétszeresével egyenlő. A példaként adott szám osztható hattal. Igaz-e, hogy az ilyen tulajdonságú számok mindegyike osztható hattal?

(6 pont)

megoldás, statisztika

K. 399. a) Hány olyan A szám van, amelyre 6⁶, 8⁸ és A legkisebb közös többszöröse 12¹²?

b) Hány olyan 1000-nél kisebb B szám van, amire 6⁶, 30³ és B legnagyobb közös osztója 3³?

(6 pont)

megoldás, statisztika

K. 400. Pisti és Kati a focipálya körül futnak, és mérik közben az időt. Pisti stoppere köridő mérésre van állítva, ami azt jelenti, hogy amikor megnyomja a gombot, az aktuális idő értékét eltárolja a stopper, és elölről kezdi a mérést. Kati stoppere részidő mérésre van beállítva, ami azt jelenti, hogy ha megnyomja a gombot, akkor a stopper eltárolja az éppen aktuális idő értékét, de folytatja tovább az idő mérését. A gyerekek négy kört futottak együtt, Kati azonban elfelejtette megnyomni az első és a harmadik kör végén a gombot, így a végén stoppere csak két időt mutatott: 164 másodpercet, és 340 másodpercet. Pisti annyit mondott az ő stoppere alapján, hogy az első kört 5 másodperccel gyorsabban futották le, mint a négy köridő átlaga, a második és harmadik köridő átlaga pedig 4 másodperccel több, mint a negyedik köridő. Mennyi idő alatt futották le a negyedik kört?

(6 pont)

megoldás, statisztika

K. 401. Az ABCD téglalapban AB=1, $BC=\sqrt 3$ . Az AB oldalra befelé, a BC oldalra kifelé szabályos háromszöget rajzolunk, így kapjuk a P, illetve Q pontokat. Mekkora az APQ háromszög területe?

(6 pont)

megoldás, statisztika

K. 402. Bizonyítsuk be, hogy két egymást követő páratlan szám reciprokait összeadva olyan törtszámot kapunk, amelynek számlálója és nevezője egy pitagoraszi számhármas két kisebb tagja.

(6 pont)

megoldás, statisztika

C-jelű feladatok

A beküldési határidő 2014. február 10-én LEJÁRT.

C. 1196. Négy testvér Mikuláskor kapott néhány zselés szaloncukrot, ám a gyerekek újra szétosztották. Olívia odaadta Péternek a cukrai felét. Péter ezután nagylelkűen továbbadta a nála levők harmadát Robinak, ő pedig továbbadta édességeinek negyedét Sárinak. Sári ekkor felkiáltott: ,,Ha Olíviának adnám cukraim ötödét, akkor mindenkinek ugyanannyi lenne!'' Hogyan osztották ki eredetileg a szaloncukrokat a gyerekeknek? Mennyi lehetett a legkevesebb szétosztott darabszám?

(5 pont)

megoldás, statisztika

C. 1197. A 64 egység területű ABCD négyzet AD oldalára illeszkedő E, és az AB oldalegyenes B csúcson túli meghosszabbítására illeszkedő F pont 50 egység területű, egyenlőszárú derékszögű háromszöget alkot a C csúccsal. Mekkora az AFE háromszög területe?

(5 pont)

megoldás, statisztika

C. 1198. Oldjuk meg az

x²+y²+1=xy+x+y

kétismeretlenes egyenletet.

(5 pont)

megoldás, statisztika

C. 1199. A mellékelt ábra burkolólapokból készített minták sorozatát mutatja. A mintákhoz használt sötétszürke lapok száma sorban: 1,6,13,24,37,....

Zsófi bebizonyította, hogy a páratlan sorszámú mintákon a sötétszürke burkolólapok száma a sorszám másodfokú függvénye. Adjuk meg, hogy hány darab sötétszürke lapot tartalmaz a kilencvenkilencedik ábra Zsófi szerint.

(5 pont)

megoldás, statisztika

C. 1200. Oldjuk meg a

$2^{\sqrt{9-4x^2}} =1-\bigg|\frac{1}{2}-\Big|\frac{1}{3}x\Big|\bigg|$

egyenletet.

(5 pont)

megoldás, statisztika

C. 1201. Az ABCD négyzet AB oldalára kifelé rajzolt AEB egyenlőszárú háromszög E csúcsnál lévő szárszöge 135^o. Legyen az AD és a BE egyenesek metszéspontja P, a CE és az AB egyenesek metszéspontja pedig Q. Igazoljuk, hogy AP=BQ.

(5 pont)

megoldás, statisztika

C. 1202. Egy henger alakú konzervdoboz alapkörének átmérője és a magassága centiméterben mérve egyenlő hosszúságú, továbbá a felszínének és a térfogatának a mérőszáma is egyenlő. Mekkora területű címke fedi be a doboz palástját?

(5 pont)

megoldás, statisztika

B-jelű feladatok

A beküldési határidő 2014. január 10-én LEJÁRT.

B. 4582. Jelölje d(n) az n pozitív egész szám pozitív osztóinak a számát. Határozzuk meg azokat az n számokat, amelyekre

d(n³)=5^.d(n).

Javasolta: Di Giovanni Márk (Győr, Révai Miklós Gimnázium)

(3 pont)

megoldás, statisztika

B. 4583. Az AB szakaszon adottak a D és E pontok. Az AD, DB, AE és EB szakaszokra ugyanabban a félsíkban emelt szabályos háromszögek harmadik csúcsai rendre F, G, H és I. Igazoljuk, hogy ha az FI és GH egyenesek nem párhuzamosak, akkor metszéspontjuk rajta van az AB egyenesen.

Javasolta: Miklós Szilárd (Herceghalom)

(3 pont)

megoldás, statisztika

B. 4584. Egy parallelogramma két átellenes csúcsán át fektessünk egy-egy olyan egyenest, amelyek a parallelogramma oldalainak meghosszabbításait két-két pontban metszik. Bizonyítsuk be, hogy ez a négy metszéspont egy trapéz négy csúcsa.

Javasolta: Moussong Gábor (Budapest)

(4 pont)

megoldás, statisztika

B. 4585. Bizonyítsuk be, hogy ha x₁ $\ge$ x₂ $\ge$ x₃ $\ge$ x₄ $\ge$ x₅ $\ge$ 0, akkor

${(x_1+x_2+x_3+x_4+x_5)}^2\ge \frac{25}{2} \big(x_4^2+x_5^2\big).$

Mi az egyenlőség feltétele?

Javasolta: Erben Péter és Pataki János (Budapest)

(3 pont)

megoldás, statisztika

B. 4586. A K, L és M az ABC háromszög AB, AC és BC oldalának olyan pontjai, melyekre KL párhuzamos BC-vel, továbbá KL=LC és $LMB\sphericalangle = BAC\sphericalangle$ . Igazoljuk, hogy LM=AK.

(Kvant)

(4 pont)

megoldás, statisztika

B. 4587. Oldjuk meg a $4^{x}-3^{x}=\mathop{\rm tg} 15^{\circ}$ egyenletet.

(3 pont)

megoldás, statisztika

B. 4588. Adott az ABC háromszög belsejében a D pont. A CD, AD és BD egyenesek az AB, BC és CA oldalakat rendre az E, F és G pontokban metszik. Az EG és AF egyenesek metszéspontja H, az EF és BG egyenesek metszéspontja pedig I. Mutassuk meg, hogy az AB, FG és HI egyenesek egy pontban metszik egymást.

Javasolta: Miklós Szilárd (Herceghalom)

(5 pont)

megoldás, statisztika

B. 4589. Létezik-e olyan n természetes szám, amelyre az $1^{10},2^{10},\ldots, n^{10}$ számok 10 csoportba oszthatók úgy, hogy mindegyik csoportban a tagok összege ugyanannyi?

(6 pont)

megoldás, statisztika

B. 4590. Adott a gömbfelületen két pont, valamint a k körvonal, ami a két pont közül pontosan az egyiken megy át. Hány olyan kör van a gömbön, amely mindkét ponton átmegy és érinti k-t?

(5 pont)

megoldás, statisztika

B. 4591. Legyen 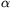$\alpha$ irracionális szám. Minden q pozitív egészre legyen $N_q(\alpha)=\min \left\{{\left|\alpha-\frac pq\right|} \colon {p \in \mathbb{Z}}\right\}$ , vagyis a legközelebbi olyan törttől való távolság, amely felírható q nevezővel (nem feltétlenül redukált alakban). Mutassuk meg, hogy létezik olyan k, amelyre

$\sum_{q=1}^{k} N_q(\alpha)>1.$

Javasolta: Maga Péter (Budapest)

(6 pont)

megoldás, statisztika

A-jelű feladatok

A beküldési határidő 2014. január 10-én LEJÁRT.

A. 602. Legyen ABC nem szabályos háromszög. Tekintsük az olyan XYZ szabályos háromszögeket, amelyek X csúcsa a BC egyenesen, Y csúcsa az AC egyenesen, Z csúcsa pedig az AB egyenesen van. Mutassuk meg, hogy az ilyen XYZ háromszögek középpontjainak mértani helye egy párhuzamos egyenespár, ami merőleges az ABC háromszög Euler-egyenesére.

Javasolta: Hraskó András (Budapest)

(5 pont)

megoldás, statisztika

A. 603. Legyen 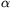$\alpha$ valós szám. Minden q pozitív egészre legyen $N_q(\alpha) = \min \left\{{\left|\alpha-\frac pq\right|} \colon {p \in \mathbb{Z}}\right\}$ , vagyis a legközelebbi olyan törttől való távolság, amely felírható q nevezővel (nem feltétlenül redukált alakban). Mutassuk meg, hogy az

$a_k= \frac{1}{\log k} \sum_{q=1}^{k} N_q(\alpha)$

sorozat konvergens.

(5 pont)

megoldás, statisztika

A. 604. Adott egy egészekből álló, (2ⁿ-1)×(2ⁿ⁺¹-1) méretű táblázat. Igazoljuk, hogy lehetséges a táblázatból 2ⁿ-1 oszlopot törölni úgy, hogy a megmaradó (2ⁿ-1)×2ⁿ-es résztáblázat minden sorában az elemek összege páros legyen.

(5 pont)

megoldás, statisztika

A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:

megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.

(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)