A KöMaL 2015. szeptemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2015. október 12-én LEJÁRT. |
M. 352. Mérjük meg egy rugós ,,ugráló béka'' rugóállandóját! A béka úgy hozható mozgásba, hogy a tapadógumit a rugó tengelyének irányában rányomjuk a korongra. (Aki nem tud ugráló békát beszerezni, egy rugós golyóstollal is elvégezheti a mérést.)

Becslési verseny, Sárospatak
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2015. október 12-én LEJÁRT. |
P. 4748. Elképzelhető-e, hogy a soproni Károly-kilátó tetejéről leejtett fagylaltgömb már a talajra érkezése előtt teljesen felolvad?
Vermes Miklós fizikaverseny, Sopron
(3 pont)
P. 4749. Egy ejtőernyős szélcsendben egyenletesen, 8 m/s sebességgel ereszkedik. Mekkora lesz az ejtőernyős sebességének nagysága, ha 6 m/s sebességű oldalszél fúj?
Jedlik Ányos fizikaverseny, Nyíregyháza
(3 pont)
P. 4750. Ezüst és arany tetszőleges arányban ötvözhető egymással. Egy ilyen ötvözet súlya levegőben 15 N, vízben 14 N. Hány tömegszázalék aranyat tartalmaz az ötvözet?
Versenyfeladat nyomán
(4 pont)
P. 4751. Mit tapasztalunk, ha egy megpendített hangvilla nyelét
\(\displaystyle a)\) az asztal lapjához érintjük, vagy
\(\displaystyle b)\) vízbe merítjük?
Magyarázzuk meg a tapasztaltakat!
Hatvani István fizikaverseny, Debrecen
(4 pont)
P. 4752. Egy íj idegét (húrját) 200 N erővel feszítjük meg, ezzel a nyilvesszőt 50 cm-rel húzzuk hátra. A feszítőerő arányos az ideg közepének kitérésével. A kihúzott íjjal függőlegesen felfelé lövünk egy 4 dkg tömegű nyilat. Legfeljebb milyen magasra szállhat fel a nyilvessző, ha a rugalmas energia 40%-a hasznosul?
Versenyfeladat nyomán
(4 pont)
P. 4753. Két orgonasíp, amelyek 80, illetve 81 cm hosszúak, 2,6 Hz-es lebegést ad, amikor mindkettő az alapfrekvencián szólal meg. Számoljuk ki a levegőben terjedő hang sebességét és a sípok alakhangjának frekvenciáját ezekből az adatokból!
Versenyfeladat nyomán
(4 pont)
P. 4754. Egy félgömb alakú, \(\displaystyle 4~{\rm dm}^3\) térfogatú rézedénybe 4 liter \(\displaystyle 30\,^\circ\)C-os vizet öntve azt tapasztaljuk, hogy a víz hőmérséklete \(\displaystyle 3\,^\circ\)C-kal csökken, az edényé viszont \(\displaystyle 27\,^\circ\)C-kal emelkedik. Mekkora az edény falának vastagsága?
Zemplén Győző fizikaverseny, Nagykanizsa
(4 pont)
P. 4755. Rendelkezésünkre áll 4 db 4,5 V-os izzólámpa, valamint egy 12 V-os és egy 3 V-os akkumulátor. Készítsünk az adott eszközök felhasználásával kapcsolást, amellyel az izzólámpák üzemi hőmérsékleten működnek!
Károly Ireneusz fizikaverseny, Esztergom
(4 pont)
P. 4756. \(\displaystyle 2a\) vastagságú, \(\displaystyle \varrho\) fajlagos ellenállású fémhuzalből \(\displaystyle r\) közepes sugarú körgyűrűt készítünk (\(\displaystyle r\gg a\)). A körvezetőt síkjára merőleges, \(\displaystyle \boldsymbol{B}_0\) indukciójú homogén mágneses mezőbe helyezzük, majd az indukciót \(\displaystyle \Delta t\) idő alatt egyenletesen nullára csökkentjük. Határozzuk meg a folyamat során indukálódó mágneses mező indukcióvektorának \(\displaystyle B_{\rm ind}\) nagyságát a körvezető középpontjában!
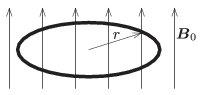
Wigner Jenő fizikaverseny, Békéscsaba
(5 pont)
P. 4757. Egy fotocellás áramkör katódjának kilépési munkája \(\displaystyle 6\cdot 10^{-19}\) J. A katód felületére merőlegesen 250 nm-es hullámhosszúságú ibolyántúli sugárzás érkezik.
\(\displaystyle a)\) Mekkora zárófeszültséggel lehet megszüntetni a fotoáramot?
\(\displaystyle b)\) Mekkora impulzust vesz fel a katód egy elemi folyamat során, ha az elektron a beeső sugárzással ellentétes irányban repül ki?
\(\displaystyle c)\) Változtassuk a sugárzás frekvenciáját! Legfeljebb hányszorosa lehet egy kilépő elektron impulzusa a beeső foton impulzusának?
Budó Ágoston fizikaverseny, Szeged
(5 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

