A KöMaL 2018. januári matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2018. február 12-én LEJÁRT. |
K. 571. Egy iskola vezetése elrendelte, hogy a tanulók nadrágszárának hossza nem lehet kisebb, mint testmagasságuk egyötöde. Samu nadrágszára hosszának ügyében vizsgálat indult, és az etikai bizottság megállapította, hogy ez éppen a megengedett minimum hossznál annak \(\displaystyle \frac{2}{7}\) részével kisebb. Sőt, azt is megállapították, hogy ha 3 cm-rel hosszabb lenne az a nadrágszár, akkor még mindig 20%-kal kisebb lenne, mint a minimális megengedett hossz. Milyen magas Samu?
(6 pont)
K. 572. Tom Sawyer és Huckleberry Finn együtt festették a kerítést. Tom egyedül 3 óra alatt, Huck egyedül 4 óra alatt festené le a kerítést. Délben kezdték a munkát, de egy idő után Huck elunta, és elindult pecázni. Tom 10 percig győzködte (ez idő alatt egyikük sem festett), de nem tudta rávenni, hogy tovább dolgozzon, így hozzávágott egy döglött patkányt, és egyedül fejezte be a munkát. 2 óra 34 perckor készen lett, és elment ebédelni. Amikor Huck és Tom együtt dolgoznak, akkor munkatempójuk 20%-kal csökken, mert folyton ugratják egymást. Mikor hagyta abba Huckleberry Finn a festést?
(6 pont)
K. 573. Kati, Sanyi és Pisti elmentek az édességboltba. Kati vett 9 egyforma bonbont karácsonyi ajándéknak, de csak \(\displaystyle 11\,000\) Ft volt nála, ezért kölcsönkérte Sanyi összes aprópénzét, így pont ki tudta fizetni a bonbonok árát. Közben Sanyinak is megtetszett ez a bonbonfajta, ezért ő is vett 13 dobozzal ajándékozásra, de mivel neki csak kereken \(\displaystyle 15\,000\) Ft-ja maradt, ezért kölcsönkérte Pisti összes aprópénzét, és így éppen ki tudta fizetni a bonbonok árát. Tudjuk, hogy egy doboz bonbon ára 0-ra végződik, és a Sanyi, illetve a Kati által kölcsönkért pénzösszeg 1000 Ft alatt volt. Mennyivel tartozik Kati Sanyinak, illetve Sanyi Pistinek?
(6 pont)
K. 574. Egy pozitív \(\displaystyle N\) számjegyeinek összege ugyanannyi, mint a szám kétszeresében a számjegyek összege.
\(\displaystyle a)\) Keressünk egy-egy ilyen kétjegyű, háromjegyű és négyjegyű számot.
\(\displaystyle b)\) Mutassuk meg, hogy \(\displaystyle N\) osztható 9-cel.
(6 pont)
K. 575. Egy összejövetelen hat ember vesz részt. Bármely három résztvevő között van kettő, aki nem ismeri egymást. Bizonyítsuk be, hogy van három olyan résztvevő közöttük, akik között nincsen ismeretség. (Az ismeretség kölcsönös.)
(6 pont)
K. 576. Egy dobozban piros és kék golyók vannak. Tudjuk, hogy \(\displaystyle \frac{2}{5}\) annak a valószínűsége, hogy a dobozból egy golyót véletlenszerűen húzva kék színű akad a kezünkbe. Ha kiveszünk a dobozból egy kék golyót, akkor \(\displaystyle \frac{5}{8}\) lesz annak a valószínűsége, hogy a dobozból egy golyót véletlenszerűen kiválasztva pirosat kapunk. Hány golyó van a dobozban?
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2018. február 12-én LEJÁRT. |
C. 1455. Egy szigeten különös pénzérmék vannak forgalomban: a pénznem alapegységei három egymástól különböző egyjegyű szám, és ezeken túl létezik az ő tízszeresük, százszorosuk, ezerszeresük. Tudjuk továbbá, hogy egy kiló kókuszdió árát ki lehet fizetni két egyforma és egy tőlük különböző harmadik pénzérme segítségével, a kétszer annyiba kerülő maracujához viszont a harmadik pénzérme helyett annak tízszeresét kell a másik kettőhöz hozzátenni. Határozzuk meg, hogy milyen értékű érmék vannak forgalomban, ha tudjuk, hogy nincsen 1-es, és a legértékesebb érme a 7000-es.
(5 pont)
C. 1456. Bizonyítsuk be, hogy nincs olyan négyzetszám, amely felírható \(\displaystyle {3^a+9^b+1}\) alakban (\(\displaystyle a\), \(\displaystyle b\) pozitív egész számok).
(5 pont)
C. 1457. Az egységsugarú körbe írt egyenlőszárú, derékszögű háromszöget a kör középpontja körül 45 fokkal elforgattuk. Határozzuk meg a két háromszög közös részének kerületét és területét.
(5 pont)
C. 1458. Oldjuk meg az egyenletet a valós számok halmazán:
\(\displaystyle \sqrt{x+11} + \sqrt{x^2+11x} -\sqrt{x} -x=4. \)
(5 pont)
C. 1459. Tükrözzük az \(\displaystyle y=x^2\) egyenletű normál parabolát az \(\displaystyle F\left(0;\frac 14\right)\) pontra. Mekkora szögben metszi egymást a két parabola?
(5 pont)
C. 1460. Egy speciális, forgásszimmetrikus hópehely képződése a következőképpen zajlik: minden másodpercben a hópehely végződéseinek felezőpontjából indulva két, egyenként harmadakkora új végződés keletkezik. (A hópehely kiinduló állapota és a képződés első két lépése az ábrán látható.) Hány darab 10 mikrométer hosszúságú végződése lesz a hópehelynek 6 másodperc elteltével, ha a hópehely átmérője 4,32 mm?
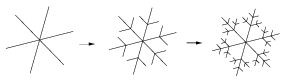
(5 pont)
C. 1461. A pozitív egész számok esetén értelmezzük a \(\displaystyle \circ\) műveletet, amelyről a következő dolgokat tudjuk: \(\displaystyle i)\) \(\displaystyle 1 \circ 1=3\); \(\displaystyle ii)\) \(\displaystyle a\circ b=b\circ a\) minden \(\displaystyle a\), \(\displaystyle b\) számra; \(\displaystyle iii)\) \(\displaystyle a \circ (b+1) = a\circ b + (a+1) + 2b\) minden \(\displaystyle a\), \(\displaystyle b\) esetén. Adjuk meg \(\displaystyle 2017\circ 2018\) értékét.
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2018. február 12-én LEJÁRT. |
B. 4921. Bizonyítsuk be, hogy ha \(\displaystyle n\) és \(\displaystyle k\) pozitív egészek, akkor \(\displaystyle n+k\) egész szám közül mindig ki lehet választani legalább \(\displaystyle (k+1)\)-et úgy, hogy az összegük \(\displaystyle n\)-nel osztható legyen.
Javasolta: Gyenes Zoltán (Budapest)
(5 pont)
B. 4922. Oldjuk meg az egész számhármasok körében a következő egyenletrendszert:
\(\displaystyle 3x-y^{2} =\frac{z}{2},\)
\(\displaystyle 3y+x^{2} =\frac{3z}{2}.\)
Javasolta: Bíró Bálint (Eger)
(3 pont)
B. 4923. Az \(\displaystyle ABC\) háromszög \(\displaystyle A\)-ból induló belső szögfelezője a \(\displaystyle BC\) oldalt \(\displaystyle E\)-ben, a \(\displaystyle B\)-ből induló belső szögfelezője az \(\displaystyle AC\) oldalt \(\displaystyle F\)-ben metszi. Jelölje \(\displaystyle O\) a háromszög beírt körének középpontját. Mekkora lehet a \(\displaystyle C\)-nél levő szög, ha az \(\displaystyle OFA\triangle\) és a \(\displaystyle OBE\triangle\) területének összege egyenlő az \(\displaystyle AOB\triangle\) területével?
(3 pont)
B. 4924. Tekintsük egy háromszög hozzáírt köreinek középpontjaiból a hozzájuk tartozó oldalakra bocsátott merőlegeseket. Igazoljuk, hogy ez a három egyenes egy pontban metszi egymást.
(4 pont)
B. 4925. Igazoljuk, hogy ha az \(\displaystyle a_1;a_2;\ldots;a_{2017}\) nemnegatív valós számok átlaga 1, akkor teljesül a következő egyenlőtlenség:
\(\displaystyle \frac{a_1}{a_1^{2018} + a_2 + a_3 + \ldots +a_{2017}} + \frac{a_2}{a_2^{2018} + a_3 + a_4 + \ldots +a_{2017} + a_1} + \ldots + \)
\(\displaystyle + \frac{a_{2017}}{a_{2017}^{2018} + a_1 + a_2 + \ldots +a_{2016}} \le 1.\)
(4 pont)
B. 4926. Az \(\displaystyle ABC\) hegyesszögű háromszögben a \(\displaystyle B\)-ből és \(\displaystyle C\)-ből induló magasság talppontja \(\displaystyle D\), illetve \(\displaystyle E\). Az \(\displaystyle E\) pont tükörképe az \(\displaystyle AC\) és a \(\displaystyle BC\) egyenesre \(\displaystyle S\), illetve \(\displaystyle T\). Az \(\displaystyle O\) középpontjú \(\displaystyle CST\) kör az \(\displaystyle AC\) egyenest másodszor az \(\displaystyle X\ne C\) pontban metszi. Mutassuk meg, hogy az \(\displaystyle XO\) és \(\displaystyle DE\) egyenesek merőlegesek egymásra.
(Koreai feladat)
(5 pont)
B. 4927. Legyen \(\displaystyle A\) és \(\displaystyle B\) vektorok egy-egy véges halmaza, továbbá legyen \(\displaystyle A+B=\{\mathbf{v} +\mathbf{w} \mid \mathbf{v}\in A\), \(\displaystyle \mathbf{w} \in B\}\). Mutassuk meg, hogy \(\displaystyle |A+B|\ge |A|+|B|-1\).
(5 pont)
B. 4928. Az égig érő fa törzse egy láb magasan kétfelé ágazik. A továbbiakban ágnak két elágazás közti részt tekintünk, amin nincs további elágazás. Az égig érő fa minden ága egyenes és egy lábbal magasabban végződik, mint a talajhoz közelebbi vége. Egy ág gyermekeinek tekintjük az ág magasabban lévő végéből kiinduló ágakat, amiket egyúttal egymás testvéreinek is nevezünk. Az égig érő fa minden ágának van legalább két gyermeke, és ha nem pont két gyermeke van, akkor van olyan testvére, akinek pontosan két gyereke van. A testvéreknek mindig különböző számú gyerekük van. Ha egy ágnak több, mint két gyereke van, akkor van olyan testvére, akinek pontosan eggyel kevesebb gyereke van, mint neki. Hány ág indul ki az \(\displaystyle n\) láb magasan lévő elágazásokból?
Javasolta: Gáspár Merse Előd (Budapest)
(6 pont)
B. 4929. Adott az \(\displaystyle \mathcal E\) ellipszis és a \(\displaystyle \mathcal H\) hiperbola a térben úgy, hogy síkjaik merőlegesek egymásra, valamint \(\displaystyle \mathcal E\) fókuszai \(\displaystyle \mathcal H\) valós tengelyének végpontjai, \(\displaystyle \mathcal H\) fókuszai pedig \(\displaystyle \mathcal E\) nagytengelyének végpontjai. Legyen \(\displaystyle A\) és \(\displaystyle B\) két rögzített pont a \(\displaystyle \mathcal H\) hiperbola különböző ágain, továbbá \(\displaystyle P\) legyen az ellipszis egy tetszőleges pontja. Mutassuk meg, hogy a \(\displaystyle PA+PB\) távolságösszeg nem függ \(\displaystyle P\) megválasztásától.
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2018. február 12-én LEJÁRT. |
A. 713. Azt mondjuk, hogy a valós számokból álló \(\displaystyle a_1,a_2,\dots\) sorozat terpeszkedő, ha minden pozitív egész \(\displaystyle j\)-re \(\displaystyle i<j\) esetén \(\displaystyle |a_i-a_j|\ge \frac1{j}\). Határozzuk meg az összes olyan \(\displaystyle C\) pozitív valós számot, melyre megadható a \(\displaystyle [0;C]\) intervallumban egy terpeszkedő sorozat.
Javasolta: Di Giovanni Márk (Cambridge)
(5 pont)
A. 714. Adottak a páronként diszjunkt \(\displaystyle D_1,D_2,\dots,D_n\) körlemezek az euklideszi síkon (\(\displaystyle n\ge 2\)). Jelölje \(\displaystyle k=1,2,\dots,n\)-re \(\displaystyle f_k\) a \(\displaystyle D_k\)-t határoló körre való inverziót. (Az \(\displaystyle f_k\) függvényt \(\displaystyle D_k\) középpontjának kivételével a sík minden pontjában értelmezzük.) Hány fixpontja lehet a sík lehető legbővebb részhalmazán értelmezett \(\displaystyle f_n\circ f_{n-1}\circ \ldots\circ f_1\) transzformációnak?
Javasolta: Váli Benedek (Szeged)
(5 pont)
A. 715. Legyenek \(\displaystyle a\) és \(\displaystyle b\) pozitív egész számok. Egy \(\displaystyle a\times b\) méretű téglalapot olyan négyzetekkel fedünk le hézagmentesen és átfedések nélkül, melyek oldalhossza \(\displaystyle 2\)-hatvány, vagyis a lefedéshez \(\displaystyle 1\times 1\)-es, \(\displaystyle 2\times 2\)-es, \(\displaystyle 4\times 4\)-es, \(\displaystyle \ldots\) méretű négyzeteket használhatunk fel. Jelölje \(\displaystyle M\) azt, hogy egy ilyen fedéshez minimálisan hány négyzetet kell felhasználnunk. Az \(\displaystyle a\) és \(\displaystyle b\) számok egyértelműen felírhatók különböző kettőhatványok összegeként: \(\displaystyle a=2^{a_1}+\ldots+2^{a_k}\), \(\displaystyle b=2^{b_1}+\ldots +2^{b_\ell}\). Mutassuk meg, hogy
\(\displaystyle M=\sum_{i=1}^k \;\sum_{j=1}^{\ell} 2^{|a_i-b_j|}. \)
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

