A KöMaL 2018. májusi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2018. június 11-én LEJÁRT. |
M. 378. Méréssel határozzuk meg, hogy egy szúnyogháló (vagy hasonló, finom szövésű anyag) hány százalékkal csökkenti az ablak fényáteresztő képességét!
Közli: Nagy Piroska Mária, Dunakeszi
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2018. június 11-én LEJÁRT. |
G. 637. Két golyót azonos kezdősebességgel, egyszerre indítunk egy-egy vízszintes, sík felületen. A mozgás során mindkét golyó legurul egy lejtőn, majd felgurul az eredeti szintre, és így jut el az út végére. Az utak hossza ugyanakkora, és a lejtők mélysége is megegyezik. A súrlódási veszteségektől mindkét esetben eltekinthetünk.
Melyik golyó ér hamarabb az út végére?
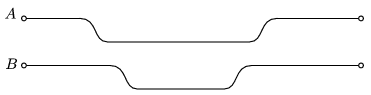
(3 pont)
G. 638. Egy kéttonnás gépkocsi kikapcsolt motorral, fékezés nélkül 36 km/h állandó sebességgel gurulna le egy 5 százalékos emelkedésű lejtőn. Mekkora a motor hasznos teljesítménye, ha ugyanezen a lejtőn, ugyanekkora sebességgel haladna felfelé ez a gépkocsi?
(3 pont)
G. 639. Megfigyelték, hogy az égő gyertya lángja a Föld körül keringő űrhajóban gömb alakú. Adjunk magyarázatot erre!
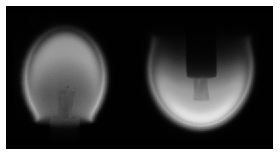
(3 pont)
G. 640. Ha a Föld \(\displaystyle R\) sugarú, homogén gömb lenne, az alábbi grafikonok közül melyik ábrázolná helyesen a gravitációs erő függését a Föld középpontjától mért távolságtól?
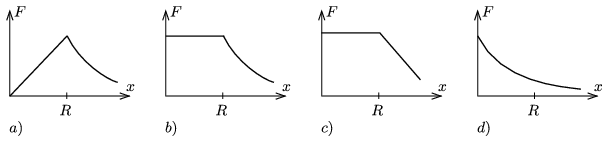
(3 pont)
 |
P-jelű feladatokA beküldési határidő 2018. június 11-én LEJÁRT. |
P. 5034. Mennyi ideig esett egy \(\displaystyle v_0\) kezdősebességgel vízszintesen elhajított test, amíg az eldobás helyétől \(\displaystyle s\) távolságra került? (A légellenállástól tekintsünk el!)
Adatok: \(\displaystyle v_0=5\) m/s, \(\displaystyle s=20\) m.
Közli: Holics László, Budapest
(4 pont)
P. 5035. Télen a cinkék egyik kedvenc eledele a magokat is tartalmazó faggyúgolyó, amelyet például egy fa alsó ágára lehet fonállal felfüggeszteni. Egy ilyen golyóból akár két cinke is falatozhat egyszerre. Egy alkalommal a 90 gramm tömegű golyón lakmározó két cinke – valamitől megriadva – egyszerre röppent fel a golyóról, ugyanakkora kezdősebességgel, egymásra merőleges irányban úgy, hogy mindkét madár kezdősebessége a vízszintessel \(\displaystyle 35^\circ\)-os szöget zárt be. Az egyenként 18 gramm tömegű cinkék közös felröppenését követően a golyót tartó függőleges fonál \(\displaystyle 10^\circ\)-kal lendült hátra, majd 1,4 másodperces lengésidővel kezdett lengedezni.
Mekkora kezdősebességgel röppentek fel a cinkék?
Közli: Radnai Gyula, Budapest
(5 pont)
P. 5036. A Nap körül keringő egyik üstökös legkisebb távolsága a Naptól 0,5 CSE, a legnagyobb pedig 31,5 CSE.
\(\displaystyle a)\) Mekkora az üstökös keringési ideje?
\(\displaystyle b)\) Mekkora területet súrol az üstököst a (nyugvónak tekinthető) Nappal összekötő szakasz egy év alatt?
Csillagászati versenyfeladat alapján
(4 pont)
P. 5037. Egy 50 cm hosszúságú, 100 g tömegű, apró szemekből álló láncot függőleges helyzetben lógatunk úgy, hogy a vége éppen egy mérleg felett helyezkedjen el. A láncot egyszer csak elengedjük.

Határozzuk meg és ábrázoljuk a mérleg által mutatott értéket a lánc tetejének a mérlegtől való távolsága, illetve az elengedés pillanatától mért idő függvényében!
A Kvant nyomán
(5 pont)
P. 5038. Két alacsony, de erős fiú áll egymás mellett. Az egyikük, András, \(\displaystyle v_0=10\) m/s kezdősebességgel, a vízszinteshez képest \(\displaystyle \alpha=30^\circ\)-os szögben eldob egy hógolyót. Társa, Bendegúz \(\displaystyle t_0=0{,}5\) s reakcióidővel később valamekkora sebességgel eldob egy másik hógolyót, és azzal még reptében el akarja találni András ,,lövedékét''. Legalább mekkora sebességgel kell Bendegúznak dobnia, hogy esélye legyen a találatra? (A terep sík, a fiúk vállmagassága \(\displaystyle h=1\) m, és a közegellenállást az egyszerűség kedvéért ne vegyük figyelembe.)
Közli: Gnädig Péter, Vácduka
(5 pont)
P. 5039. Két könnyű, merev pálca hossza \(\displaystyle \ell_1\), illetve \(\displaystyle \ell_2\). Egyik végükhöz \(\displaystyle m_1\), illetve \(\displaystyle m_2\) tömegű, kis méretű testet erősítünk, másik végüket mereven összekötjük úgy, hogy a pálcák egymással bezárt szöge \(\displaystyle \alpha\) legyen. Ez a rendszer az összekötési ponton átmenő, vízszintes tengely körül szabadon lenghet a pálcák által meghatározott síkban. Mekkora az egyensúlyi helyzetéből kissé kitérített rendszer lengésideje?
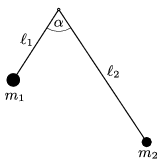
Példatári feladat
(5 pont)
P. 5040. Az \(\displaystyle 50~{\rm m}^2\) alapterületű és 3 m belmagasságú tanteremben nyitott ajtó mellett a diákok éppen dolgozatot írnak. A hőmérséklet \(\displaystyle 24~{}^\circ\)C, a légnyomás \(\displaystyle 10^5\) Pa. Adjunk becslést a következő mennyiségekre:
\(\displaystyle a)\) Mekkora a teremben található levegő tömege?
\(\displaystyle b)\) Mekkora a teremben található levegő belső energiája?
\(\displaystyle c)\) Mennyivel változna a teremben található levegő belső energiája, ha a hőmérséklet \(\displaystyle 2~^\circ\)C-kal emelkedne?
Közli: Széchenyi Gábor, Budapest
(4 pont)
P. 5041. Vízszintes síkban, egymástól \(\displaystyle L= 10\) cm távolságra két párhuzamos, elhanyagolható ellenállású, rögzített sín van, amelyeket az ábra szerint az egyik végüknél \(\displaystyle U_0= 0{,}3\) V-os, állandó feszültségű áramforrás kapcsol össze. A ,,berendezés'' függőlegesen lefelé mutató, \(\displaystyle B=1\) T indukciójú, homogén mágneses mezőben van. A sínekre merőlegesen \(\displaystyle R=0{,}2~\Omega\) ellenállású fémpálcát fektettünk, ami a síneken súrlódásmentesen mozoghat.
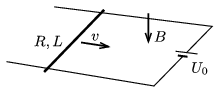
Mekkora nagyságú és milyen irányú erőt kell a sínekkel párhuzamosan kifejteni a pálcára, hogy az az ábrán jelzett irányban állandó \(\displaystyle v\) sebességgel mozogjon, ha
\(\displaystyle a)\) \(\displaystyle v=1\) m/s;
\(\displaystyle b)\) \(\displaystyle v=5\) m/s?
\(\displaystyle c)\) Mekkora a telep által leadott teljesítmény a két esetben?
Közli: Zsigri Ferenc, Budapest
(5 pont)
P. 5042. Egy hagyományos optikai rácsra merőlegesen olyan bíborszínű fényt bocsátunk, amely 652 nm hullámhosszú vörös és 489 nm hullámhosszú kék fény keveréke. A 2 m távolságra lévő ernyőn megfigyelhető legközelebbi bíborszínű fényfoltok távolsága 20 cm. Mekkora a rácsállandó?
Közli: Vigh Máté, Budapest
(4 pont)
P. 5043. Egy \(\displaystyle 1{,}6\cdot 10^{-13}\) J mozgási energiájú deutérium álló tríciumba ütközik. A lejátszódó magreakció:
\(\displaystyle {}^2_1{\rm H}+ {}^3_1{\rm H}\rightarrow {}^4_2{\rm He}+ {}^1_0{\rm n}. \)
A kilépő neutron sebessége a deutérium sebességének irányával \(\displaystyle 60^\circ\)-os szöget zár be.
\(\displaystyle a)\) Mennyi energia szabadul fel?
\(\displaystyle b)\) Mennyi lesz az \(\displaystyle \alpha\)-részecske és a neutron mozgási energiája az ütközés után?
\(\displaystyle c)\) Mekkora szöget zár be az \(\displaystyle \alpha\)-részecske sebessége a deutérium sebességével?
(Az izotóptömegek táblázata megtalálható honlapunkon a www.komal.hu/cikkek/atomtomegek.pdf címen.)
Közli: Kobzos Ferenc, Dunaújváros
(5 pont)
P. 5044. András és Béla ikertestvérek. A 20. születésnapjukon sorsuk megváltozik: András a Földön marad, Béla viszont egy hosszabb űrexpedícióra indul. Az űrhajó állandó sebességgel távolodik a Földtől. Egy év múlva András készít egy fényképet a születésnapi tortájáról, és rádiójelekkel elküldi azt Bélának, aki azt épp a 22. születésnapján kapja meg az űrhajóban.
\(\displaystyle a)\) Mekkora sebességgel távolodik az űrhajó a Földtől?
\(\displaystyle b)\) Milyen távol van az űrhajó a Földtől András szerint a fénykép megérkezésekor?
\(\displaystyle c)\) Béla is készít egy felvételt a 22. születésnapjáról, és azonnal elküldi azt testvérének. Hány éves korában kapja meg András ezt a fényképet?
Közli: Simon Péter, Pécs
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

