A KöMaL 2021. novemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2021. december 15-én LEJÁRT. |
M. 408. Ütköztessük egymással befőttesüvegek különböző méretű csavaros fedeleit úgy, hogy az egyik áll, a másik pedig egyenesen ütközik vele. Határozzuk meg az ütközés rugalmasságának mértékét jellemző ütközési számot!
Varga István (1952–2007) feladata
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2021. december 15-én LEJÁRT. |
G. 757. Van egy pár kifordítható kesztyűm, mindkét darabja kívül fekete, belül fehér. Tudom-e ezeket felemás kesztyűként hordani?
Közli: Vladár Károly, Kiskunhalas
(3 pont)
G. 758. Egy személygépkocsi mögötti, nem túl messze lévő tárgyat egyszerre láthatjuk az autó két oldalsó, valamint a középső (belső) visszapillantó tükrében. Mindhárom tükör sík. Melyik tükörben látja a vezető a tárgy képét legnagyobbnak, illetve legkisebbnek? Másképp fogalmazva, hasonlítsuk össze a három kép látószögét!
(3 pont)
G. 759. Egy vízszintes, súrlódásmentes, rögzített pálcára felfűzve négy darab \(\displaystyle m\) tömegű, négy darab \(\displaystyle M\) tömegű \(\displaystyle (m<M)\), majd ismét egy \(\displaystyle m\) tömegű, tökéletesen rugalmas golyó áll közel egymáshoz az ábrán látható elrendezésben. Balról egy \(\displaystyle m\) tömegű, szintén tökéletesen rugalmas golyó érkezik \(\displaystyle v\) sebességgel, és ütközik a golyósor első tagjával.
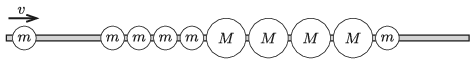
A további ütközések lezajlása után mely golyók maradnak nyugalomban, és a többiek milyen irányban fognak mozogni?
(4 pont)
G. 760. Alumíniumból készült, 10 cm magas, kúp alakú testet a csúcsához rögzített fonál segítségével lassan kiemelünk egy téglatest alakú akváriumból. Kezdetben a kúp a 10 cm átmérőjű alapkörén áll az akvárium alján, és a víz teljesen ellepi. Az akvárium térfogata sokkal nagyobb, mint az alumíniumkúpé.
Ábrázoljuk a fonalat feszítő erőt a kúp elmozdulásának függvényében!
A KöMaL Nyári Tábor mérési feladata nyomán
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2021. december 15-én LEJÁRT. |
P. 5355. Újsághír (2021. február 24.): A kínai Mars-szonda, a Tienven-1 már a Mars körül kering, és adatokat gyűjt a vörös bolygóról. Parkolási pályájának a Mars felszínétől mért legtávolabbi pontja 59 ezer kilométerre, míg a legközelebbi 280 kilométerre van. A szonda két marsi nap alatt tesz meg egy ,,kört'' a bolygó körül.
Számítással ellenőrizzük, hogy milyen pontossággal igaz a keringési időre megadott érték, ha a többi adatot helyesnek fogadjuk el!
Közli: Gnädig Péter, Vácduka
(4 pont)
P. 5356. Vízszintes talajon fekszik egy téglalap keresztmetszetű gerenda. A téglalap vízszintes oldala \(\displaystyle L\), függőleges oldala \(\displaystyle H\) hosszúságú. Elhanyagolva a közegellenállást, honnan és hogyan kell elugrania egy szöcskének, hogy a lehető legkisebb energiaráfordítással sikerüljön átugrania ezt a gerendát? Hol lesz az ugrási parabola fókuszpontja ebben az esetben?
Radnai Gyula (1939–2021) feladata
(5 pont)
P. 5357. Vízszintes asztallapon fekszik egy homogén tömegeloszlású rúd. Ezt a rudat lassan függőleges helyzetbe hozzuk az egyik végére ható, a rúdra mindenkor merőleges erővel. Legalább mekkora a rúd és az asztallap közötti tapadási súrlódási együttható, ha a rúd nem csúszik meg felállítás közben?
Amerikai feladat nyomán
(5 pont)
P. 5358. Hosszú, vékony, függőlegesen kifeszített szigetelőszálon két gyöngy közül az egyik rögzített, a másikat pedig efölött \(\displaystyle h = 0{,}5\) m magasságban tartjuk.
A felső gyöngy tömege \(\displaystyle m = 0{,}5\) gramm, mindkét gyöngy elektromos töltése \(\displaystyle Q = 2{,}6\cdot 10^{-7}\) C. Egy adott pillanatban a felső gyöngyöt lökésmentesen elengedjük.
\(\displaystyle a\)) Mekkora utat tesz meg a gyöngy a legnagyobb sebesség eléréséig?
\(\displaystyle b)\) Mekkora ez a sebesség?
\(\displaystyle c)\) Mekkora lesz a két gyöngy közötti minimális távolság?
\(\displaystyle d)\) Mekkora a pálya legalsó pontjában a gyöngy gyorsulása?
Közli: Holics László, Budapest
(4 pont)
P. 5359. Egy kocka élei kétféle ellenállásból épülnek fel. Valamelyik két szemközti laphoz tartozó 8 db él ellenállásának értéke \(\displaystyle r\), míg az ezekre merőleges 4 db élt alkotó ellenállások értéke \(\displaystyle R\). Határozzuk meg a hálózat eredő ellenállását az egyik \(\displaystyle R\) ellenállást közrefogó, két szomszédos csúcspont között!
Közli: Szekeres Béla, Budapest
(4 pont)
P. 5360. Demonstráció céljából egyszerű Kepler-távcsövet készítünk. Ehhez rendelkezésünkre áll két gyűjtőlencse: egy \(\displaystyle D\) átmérőjű, \(\displaystyle f_1\) fókusztávolságú objektív és egy \(\displaystyle d\) átmérőjű, \(\displaystyle f_2\ll f_1\) fókusztávolságú szemlencse, valamint egy, a távcső tubusában a lencsék közös fókuszsíkjában rögzíthető blende (más néven: fényrekesz). Ezzel szeretnénk szabályozni a távcső képalkotásában szerepet játszó sugárnyalábokat.
\(\displaystyle a)\) Mekkora a blende nélküli távcső látómezeje szögben kifejezve (azaz legfeljebb milyen szögtávolságra lehet két csillag akkor, ha egyszerre láthatók a távcsőben)?
\(\displaystyle b)\) Legfeljebb mekkorára választhatjuk a ,,látómező határoló blende'' nyílásának átmérőjét ahhoz, hogy a távcső fényerő szempontjából ne torzítson (azaz a kép szélének megfelelő irányokból is minden fény, ami az objektívre esik, átjusson a szemlencsén is)? Mekkora lehet így a távcső látómezeje?
Útmutatás: Vizsgáljuk az optikai tengelyhez képest különböző irányokból az objektívre érkező párhuzamos fénynyalábok alakulását, ahogy áthaladnak a távcsövön! A távcső kilépő pupillája (az objektív átmérője osztva a szögnagyítással) kisebb, mint a szemlencse átmérője.
Közli: Woynarovich Ferenc, Budapest
(5 pont)
P. 5361. Az alábbi két képen ugyanazt az autót látjuk, ugyanabban az időben. Az első képen függönyön keresztül, a másodikon függöny nélkül. Az autó 20 méterre volt a függönytől.

Milyen sűrű szövésű lehet a függöny?
Tichy Géza (1945–2021) feladata
(5 pont)
P. 5362. Szinkrociklotronban az elemi részecskék tömegének a sebességtől való függését a gyorsító elektromos tér frekvenciájának csökkentésével kompenzálják. Például ha protonokat gyorsítanak, a duánsokra (D alakú, fémből készült, üreges félkorongokra) kerülő feszültség frekvenciáját 25 MHz-ről 18,9 MHz-ig változtatják ciklusonként. Határozzuk meg ebben az esetben
\(\displaystyle a)\) a mágneses indukcióvektor nagyságát;
\(\displaystyle b)\) a kilépő protonok kinetikus energiáját!
Példatári feladat nyomán
(5 pont)
P. 5363. Egy vékony, magas üvegcsőből homokórát készítettünk. A benne lévő homok \(\displaystyle m_0\) tömege megegyezik az üvegcső és a tartótalpak együttes tömegével. Kezdetben a homok az alsó térfél \(\displaystyle h=5\) cm hosszú részét tölti ki, és az eszköz megfordítása után egyenletes ütemben \(\displaystyle t_0= 1\) perc alatt pereg le. (A felső és az alsó térfélben lévő homok alakját közelítsük hengerekkel.)

\(\displaystyle a)\) Határozzuk meg, hogy hol van a homokóra tömegközéppontja \(\displaystyle t\) idővel az óra elindítása után! (Ne foglalkozzunk a homokóra indítását követő, illetve a megállását közvetlenül megelőző nagyon rövid időtartamokkal, amikor a homokzuhatag még vagy már nem tölti ki a kifolyónyílás és az alsó becsapódási hely közötti teljes távolságot.)
\(\displaystyle b)\) Számítsuk ki, hogy mekkora a homokóra impulzusa (lendülete) \(\displaystyle t\) idővel a homokóra elindítása után!
\(\displaystyle c)\) Nagyon érzékeny mérleggel megmérjük a homokóra súlyát, miközben a homok a felső tartályból az alsóba pereg. Azt találjuk, hogy a mért súly egy kicsivel nagyobb, mint a már lepergett homokóra súlya. Az előző két részfeladatra adott választ felhasználva adjuk meg, hogy hány ezrelékkel nagyobb a működő homokóra súlya a már ,,lejárt'' homokóráénál!
Közli: Széchenyi Gábor, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

