The ellipse
 |
 |
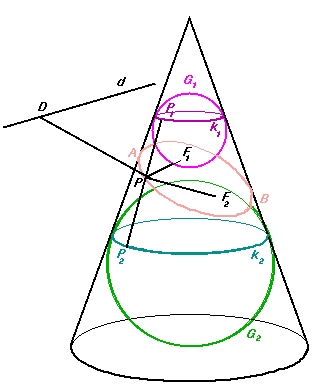
Let P be an arbitrary point of the conic section. Consider the two spheres which touch the cone and the plane. Let sphere G1 and G2 touch the cone at circles k1 and k2, and the plane at points F1 and F2, respectively. Let the generator through P intersect k1 and k2 at P1 and P2, respectively. As PP1=PF1 and PP2=PF2, PF1+PF2=P1P2. Since the line segment P1P2 is bounded by circles k1 and k2, its length does not depend on the choice of point P. Hence,
For all points P of the conic, PF1+PF2 is constant; and thus, by the definition, the conic is an ellipse.
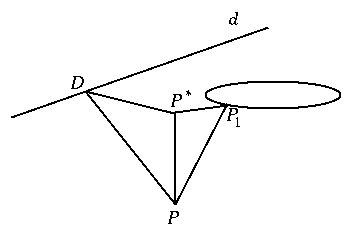
We can use the spheres to prove another important property of the ellipse. Let the intersection of the planes of circle k1 and the ellipse be line d, and let D and P* be the projections of P to d and to the plane of of circle k1, respectively. It is easy to see that the triangles PP*P1 are similar for all choices of P, thus the ratio of distances PP* and PP1=PF1 is constant. The triangles PP*D are also similar, which yields that the ratio of PP* and PD is another constant. Putting the results together, we obtain that
The ratio of the distance of P from the focus F1 to the distance from the line d is constant.
The constant is less than 1, because angle P*PP1 is the half of the apex angle of the cone, and angle P*PD is greater.
 |
