A hiperbola
 |
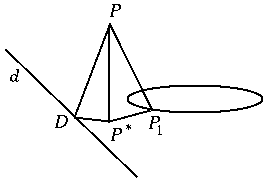 |
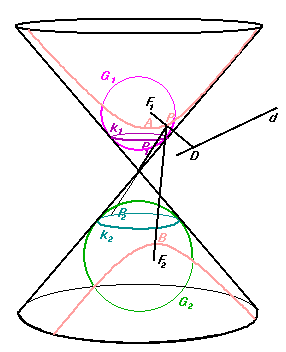
Legyen P a síkmetszet egy tetszőleges pontja. Illesszünk a kúpba olyan gömböket, amik érintik a kúpot és a metszősíkot is. A G1 gömb a kúp palástját k1 körben, a síkot F1 pontban érinti. A G2 gömb a kúpot k2 körben, a metszősíkot F2 pontban érinti. P-ből húzzunk a gömbökhöz érintőszakaszokat! Teljesül rájuk, hogy PP1=PF1 és PP2=PF2. Ugyanakkor PP1 és PP2 egy, közös alkotón vannak. A PP2 PP1-n kívüli alkotódarabját k1 és k2 körök határolják. A síkmetszetnek bármely pontjáról legyen is szó, a gömbökhöz rajzolt érintőszakaszok különbsége a paláston mindig a két kör között helyezkedik el, nagysága így állandó. Másrészről az érintési tulajdonság miatt a síkbeli érintőszakaszok hosszának különbsége, |PF1-PF2|=|PP1+PP2| is állandó nagyságú. Ezzel kaptunk két adott pontot: F1-t és F2-t, amelyektől mért távolságkülönbsége P-nek mindig ugyanakkora. Definíció szerint síkmetszetünk egy hiperbola.
A hiperbola egy másik, szintén "ponthalmazos" definíciójához is eljuthatunk a kúp metszésével. Messe ugyanis k1 kör síkja a metszősíkot d egyenesben. P-ből merőlegest állítva d-re, D talppontot kapjuk, az első kör síkjára állítva P* pontot nyerjük. Az így keletkezett PP*P1 háromszög derékszögű, P-nél levő szöge a kúp félnyílásszöge, tehát minden hiperbolapontból szerkesztett háromszögre ugyan akkora. Ezek a derékszögű háromszögek hasonlóak. Másrészről d-re állított merőlegesek - bármely hiperbolapontból indítva - a metszősíkban vannak és párhuzamosak. Most a DPP* háromszögeket vizsgálva, ha P befutja az ellipszis pontjait, derékszögűek és a párhuzamosállású szögeik miatt hasonlóak egymáshoz. Tehát \(\displaystyle PP_1={PP^*\over a}\) és \(\displaystyle PD={PP^*\over b}\), ahol a konstansok a megfelelő bezárt szögek cosinusai. Ekkor \(\displaystyle {PP_1\over PD}={PF_1\over PD}={b\over a}\) szögektől függő állandó. Vizsgálatunk eredménye, hogy a hiperbola pontjaira teljesül, hogy egy adott ponttól (fókusz) és egy adott egyenestől (direktrix) mért távolságuk hányadosa állandó, ami a konstrukció miatt 1-nél nagyobb.
 |
