The parabola
 |
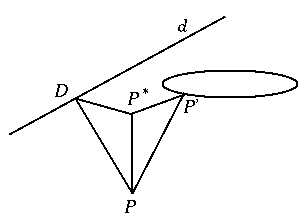 |
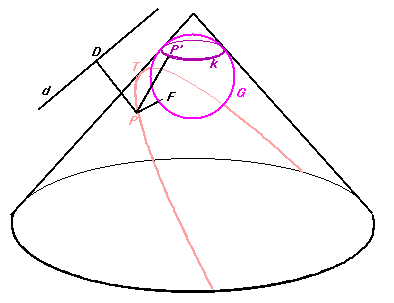
Let P be an arbitrary point of the conic. Consider the sphere G which touches the plane of the conic and the cone at the point F and at circle k, respectively. Let the generator through P intersect k at point P'. Let the intersection of the planes of circle k and the conic be line d, and let D and P* be the projections of P to d and to the plane of circle k, respectively. The angles P*PP' and P*PD are equal to the half of the apex angle of the cone, which yields that PD=PP'=PF. Hence,
Each point P of the conic is equidistant from point F and line d; and thus, by the definition, the conic is a parabola.
 |
