KöMaL Problems in Mathematics, October 2023
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on November 10, 2023. |
K. 779. Given a four-digit number, the following transformations are allowed in each step:
1. We may change the order of the digits as we wish.
2. We may increase each of the first two digits by 1.
Starting out from 2024, what is the least number of steps needed to obtain the number 7654?
(5 pont)
solution (in Hungarian), statistics
K. 780. \(\displaystyle a)\) Is it possible to obtain a prime number as a result if two prime numbers are both added to their product? If so, give at least three examples. If not, explain why it is not possible.
\(\displaystyle b)\) Is it possible to obtain a prime number as a result if two prime numbers are both added to their product, and then 1 is added to the sum? If so, give at least three examples. If not, explain why it is not possible.
(5 pont)
solution (in Hungarian), statistics
K. 781. The numbers \(\displaystyle 1\), \(\displaystyle 2\), \(\displaystyle 3\), \(\displaystyle 4\), \(\displaystyle 5\), \(\displaystyle 6\) are entered in the fields of each of two \(\displaystyle 2\times3\) tables, one red and one green. Within each table, every number occurs exactly once. Then the numbers in the corresponding fields of the two tables are added, and a third table is formed with them. See the example below.
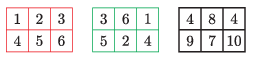
Fill in the given red and green tables so that the table on the right, with the lower right corner hidden, should be obtained by performing the addition. Find all possible solutions.
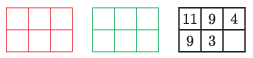
(5 pont)
 |
Problems with sign 'K/C'Deadline expired on November 10, 2023. |
K/C. 782. Archibald did not remember the correct way of adding fractions, and added the fractions \(\displaystyle \frac ab\) and \(\displaystyle \frac cd\) as follows: \(\displaystyle \frac ab + \frac cd = \frac{a+c}{b+d}\). Is it possible that he obtained a correct answer if \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle d\) are positive numbers?
(5 pont)
solution (in Hungarian), statistics
K/C. 783. Pilots refer to directions by using the face of a clock. For example, they say 12 o'clock instead of north, 3 o'clock instead of east. Follow the flight of a reconnaissance aeroplane that started from the army base on the ground, flew 1 minute in the direction of 1 o'clock, 2 minutes in the direction of 2 o'clock, 3 minutes in the direction of 3 o'clock, 10 minutes in the direction of 4 o'clock, 5 minutes in the direction of 5 o'clock, 6 minutes in the direction of 6 o'clock, 7 minutes in the direction of 7 o'clock, 8 minutes in the direction of 8 o'clock, 9 minutes in the direction of 9 o'clock, 4 minutes in the direction of 10 o'clock, 11 minutes in the direction of 11 o'clock, and 12 minutes in the direction of 12 o'clock. The speed of the plane relative to the ground remained the same throughout. What path would have been the shortest from the starting point to the final destination?
(5 pont)
 |
Problems with sign 'C'Deadline expired on November 10, 2023. |
C. 1778. Find all integers \(\displaystyle n\) for which \(\displaystyle 1+2+3+\cdots +n\), in decimal notation, equals a three digit number of identical digits.
(Vietnamese problem)
(5 pont)
solution (in Hungarian), statistics
C. 1779. Prove that there exist infinitely many triangles in which the lengths of the sides are
\(\displaystyle \frac{3x}{2};\quad 2x-1;\quad 3x+1 \)
where \(\displaystyle x\) is a positive integer. Determine the length of the sides in the triangle of the smallest perimeter.
Proposed by B. Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
C. 1780. Are there ordered pairs \(\displaystyle (a;b)\) of positive integers for which both \(\displaystyle a^2-2b\) and \(\displaystyle b^2-2a\) are perfect squares?
German competition problem
(5 pont)
solution (in Hungarian), statistics
C. 1781. Solve the simultaneous equations
$$\begin{align*} 3x+\sqrt{y^2-21y} & =2x^2,\\ x^2-x-\sqrt{y^2-21y} & =x^3 \end{align*}$$over the set of real number pairs.
Proposed by B. Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
C. 1782. From vertex \(\displaystyle D\) of a square \(\displaystyle ABCD\), a tangent is drawn to the semicircle of diameter \(\displaystyle AB\) lying inside the square. The point of tangency (different from point \(\displaystyle A\)) is \(\displaystyle E\), and the midpoint of line segment \(\displaystyle AB\) is \(\displaystyle F\). The tangent intersects line \(\displaystyle BC\) at point \(\displaystyle G\) and line \(\displaystyle AB\) at point \(\displaystyle H\). Line \(\displaystyle EF\) intersects line \(\displaystyle DA\) at point \(\displaystyle K\). Prove that the radii of the inscribed circles of triangles \(\displaystyle FHE\), \(\displaystyle DGC\) and \(\displaystyle DKE\), in this order, form three consecutive terms of an increasing arithmetric sequence.
Proposed by B. Bíró, Eger
(5 pont)
 |
Problems with sign 'B'Deadline expired on November 10, 2023. |
B. 5334. What is the smallest \(\displaystyle n\) for which every convex \(\displaystyle n\)-gon has two adjacent obtuse angles?
Paul Erdős, 1913–1996
(3 pont)
solution (in Hungarian), statistics
B. 5335. The product of the positive numbers \(\displaystyle x\), \(\displaystyle y\), \(\displaystyle z\) is 1. What may be the value of the expression
\(\displaystyle \left(x+\frac{1}{x}\right)^{2} +\left(y+\frac{1}{y}\right)^{2} +\left(z+\frac{1}{z}\right)^{2} -\left(x+\frac{1}{x}\right) \left(y+\frac{1}{y}\right) \left(z+\frac{1}{z}\right)? \)
Proposed by G. Kiss, Csömör
(3 pont)
solution (in Hungarian), statistics
B. 5336. The organizers of a school event bought four kinds of sweets to use them as awards for correct answers. The prices paid for them were \(\displaystyle 1300\) forints (HUF, Hungarian currency), \(\displaystyle 3000\) forints, \(\displaystyle 3300\) forints and (for questions for the audience) a large number of sweets for \(\displaystyle 50\) forints a piece.
The total was \(\displaystyle 41\,300\) forints, and the mean price per item was exactly \(\displaystyle 100\) forints. How many of each kind did they buy?
Proposed by G. Kiss, Csömör
(4 pont)
solution (in Hungarian), statistics
B. 5337. A regular triangle is drawn over each side of a regular \(\displaystyle n\)-gon, on the outside. The third vertices of the triangles form a larger \(\displaystyle n\)-gon. What may the number \(\displaystyle n\) be if the ratio of the areas of the two polygons is an integer?
Proposed by B. Hujter, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 5338. There are 10 numbered seats in a particular row of an auditorium. The seats are accessible from each end of the row. The 10 spectators holding tickets for that row arrive in a random order and they take their seats. Since the spectators do not like passing others already seated, they will approach their seats from the direction where that can be avoided, if possible. Determine the probability that at least one of the 10 ticket holders will not be able to access their seat without passing a seated spectator.
Proposed by L. Koncz, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 5339. A circle \(\displaystyle k_1\) touches another circle \(\displaystyle k_2\) from the inside at point \(\displaystyle P\). Let \(\displaystyle M\) denote an arbitrary point on the circumference of \(\displaystyle k_1\), and let the tangent drawn to \(\displaystyle k_1\) at \(\displaystyle M\) intersect \(\displaystyle k_2\) at points \(\displaystyle A\) and \(\displaystyle B\). Show that \(\displaystyle PM\) bisects the angle \(\displaystyle APB\).
(4 pont)
solution (in Hungarian), statistics
B. 5340. Let \(\displaystyle n\) be a positive integer, and let \(\displaystyle f\), \(\displaystyle g\) and \(\displaystyle h\) denote polynomials with real coefficients whose degrees are at most \(\displaystyle n\). What is the largest possible number of real numbers \(\displaystyle x\) for which \(\displaystyle f(x)\), \(\displaystyle g(x)\), \(\displaystyle h(x)\), in some order, are consecutive terms of a non-constant arithmetic sequence, assuming that there are only a finite number of such \(\displaystyle x\)?
Proposed by P.\(\displaystyle \,\)P. Pach, Budapest
(6 pont)
solution (in Hungarian), statistics
B. 5341. The centroid of a regular tetrahedron \(\displaystyle ABCD\) is \(\displaystyle S\), and an arbitrary interior point is \(\displaystyle P\). Reflect point \(\displaystyle P\) in the planes of the four faces of the tetrahedron to obtain tetrahedron \(\displaystyle XYZW\). Show that the centroid of \(\displaystyle XYZW\) is the point that divides line segment \(\displaystyle PS\) in the ratio \(\displaystyle 2:1\), with the shorter piece next to \(\displaystyle S\).
Based on a problem from Monthly
(6 pont)
 |
Problems with sign 'A'Deadline expired on November 10, 2023. |
A. 860. A 0\(\displaystyle \,\)–\(\displaystyle \,\)1 sequence of length \(\displaystyle 2^k\) is given. Alice can pick a member from the sequence, and reveal it (its place and its value) to Bob. Find the largest number \(\displaystyle s\) for which Bob can always pick \(\displaystyle s\) members of the sequence, and guess all their values correctly.
Alice and Bob can discuss a strategy before the game with the aim of maximizing the number of correct guesses of Bob. The only information Bob has is the length of the sequence and the member of the sequence picked by Alice.
Submitted by Gábor Szűcs, Szikszó
(7 pont)
A. 861. Let \(\displaystyle f(x)=x^2-2\). Let \(\displaystyle f^{(n)}(x)\) denote the \(\displaystyle n^{\text{th}}\) iterate of \(\displaystyle f\) (i.e. \(\displaystyle f^{(1)}(x)=f(x)\) and \(\displaystyle f^{(k+1)}(x)=f\big(f^{(k)}(x)\big)\)).
Let \(\displaystyle H=\big\{x\colon f^{(100)}(x)\le -1\big\}\). Find the length of \(\displaystyle H\) (the sum of the lengths of the intervals in \(\displaystyle H\)). We expect the solution as a closed-form expression.
Submitted by Dávid Matolcsi, Budapest
(7 pont)
A. 862. Let \(\displaystyle ABCD\) be a cyclic quadrilateral inscribed in circle \(\displaystyle \omega\). Let \(\displaystyle F_A\), \(\displaystyle F_B\), \(\displaystyle F_C\) and \(\displaystyle F_D\) be the midpoints of arcs \(\displaystyle AB\), \(\displaystyle BC\), \(\displaystyle CD\) and \(\displaystyle DA\) of \(\displaystyle \omega\). Let \(\displaystyle I_A\), \(\displaystyle I_B\), \(\displaystyle I_C\) and \(\displaystyle I_D\) be the incenters of triangles \(\displaystyle DAB\), \(\displaystyle ABC\), \(\displaystyle BCD\) and \(\displaystyle CDA\), respectively.
Let \(\displaystyle \omega_A\) denote the circle that is tangent to \(\displaystyle omega\) at \(\displaystyle F_A\) and also tangent to line segment \(\displaystyle CD\). Similarly, let \(\displaystyle \omega_C\) denote the circle that is tangent to \(\displaystyle \omega\) at \(\displaystyle F_C\) and tangent to line segment \(\displaystyle AB\).
Finally, let \(\displaystyle T_B\) denote the second intersection of \(\displaystyle \omega\) and circle \(\displaystyle F_BI_BI_C\) different from \(\displaystyle F_B\), and let \(\displaystyle T_D\) denote the second intersection of \(\displaystyle \omega\) and circle \(\displaystyle F_DI_DI_A\).
Prove that the radical axis of circles \(\displaystyle \omega_A\) and \(\displaystyle \omega_C\) passes through points \(\displaystyle T_B\) and \(\displaystyle T_D\).
Submitted by Géza Kós, Budapest
(7 pont)
Upload your solutions above.
