KöMaL Problems in Mathematics, December 2023
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on January 10, 2024. |
K. 789. We color the positions of the integers on the number line using red and blue dots.
\(\displaystyle a)\) Is it possible to find a coloring such that no two dots with the same color are exactly 5 or 7 units apart from each other?
\(\displaystyle b)\) Is it possible to find a coloring such that no two dots with the same color are exactly 6 or 11 units apart from each other?
(5 pont)
solution (in Hungarian), statistics
K. 790. The 100 richest people of Neverland had a dinner party in a room with 12 huge tables. Those with birthdays in the same month sat down at the same table. Let \(\displaystyle X\) denote the number of people around the table with the smallest number of people. Let \(\displaystyle Y\) denote the number of people around the table with the largest number of people. Find the greatest possible value of \(\displaystyle X\) and the smallest possible value of \(\displaystyle Y\).
(5 pont)
solution (in Hungarian), statistics
K. 791. \(\displaystyle a)\) Find all three digit numbers that are equal to four times the product of their digits.
\(\displaystyle b)\) Is it possible to find a three digit number that is equal to twice the product of its digits?
(5 pont)
 |
Problems with sign 'K/C'Deadline expired on January 10, 2024. |
K/C. 792. Let \(\displaystyle n\) be a positive integer. Prove that the last digit of the sum \(\displaystyle 1+2+3+\cdots+n\) cannot be 2, 4, 7 or 9.
(5 pont)
solution (in Hungarian), statistics
K/C. 793. We have to fill in the \(\displaystyle 3\times 4\) table in the figure with \(\displaystyle X\)'s obeying the following rule: if there are exactly two \(\displaystyle X\)'s in the same row or column, we can put a third \(\displaystyle X\) in one of the empty cells in the row or column of the two \(\displaystyle X\)'s. Prove that regardless of the order we choose, we will be left with at least two empty cells in the end.
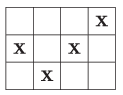
(5 pont)
 |
Problems with sign 'C'Deadline expired on January 10, 2024. |
C. 1788. Solve the equation \(\displaystyle 14x^2+15y^2=7^{2023}\) for integer values of \(\displaystyle x\) and \(\displaystyle y\).
(Based on a Swiss competition problem)
(5 pont)
solution (in Hungarian), statistics
C. 1789. A tortoise travelled a distance of \(\displaystyle 14\) units in the plane. Each of its steps were of a unit's length. After each step it made a turn: if the number of the previous step was odd, then with an angle of \(\displaystyle 60^{\circ}\), if even, then with an angle of \(\displaystyle 90^{\circ}\). In steps \(\displaystyle 3\), \(\displaystyle 5\), \(\displaystyle 8\) and \(\displaystyle 12\) he turned to the right, in the remaining steps he turned to the left.
\(\displaystyle a)\) Prove that the tortoise will end up in its initial position facing in its initial direction after its \(\displaystyle 14^{\text{th}}\) step.
\(\displaystyle b)\) Find the area enclosed by the walk of tortoise in algebraic form.
Submitted by Lajos Szilassi, Szeged
(5 pont)
solution (in Hungarian), statistics
C. 1790. Find the smallest possible value of the expression \(\displaystyle x^2+y^2+5z^2-xy-3yz-zx+3x-4y+7z\) for real values of \(\displaystyle x\), \(\displaystyle y\) and \(\displaystyle z\).
Vietnamese problem
(5 pont)
solution (in Hungarian), statistics
C. 1791. Solve the equation
\(\displaystyle \frac{8^x - 15 625}{4^x + 25 \cdot 2^x + 625} = 2023\)
for real values of \(\displaystyle x\).
Submitted by Olivér Teleki, Tököl
(5 pont)
solution (in Hungarian), statistics
C. 1792. In triangle \(\displaystyle ABC\) let the midpoints of sides \(\displaystyle AB\) and \(\displaystyle AC\) be \(\displaystyle F\) and \(\displaystyle E\), respectively. Let \(\displaystyle P\) and \(\displaystyle Q\) be two arbitrary points in the plane of triangle \(\displaystyle ABC\). Let \(\displaystyle P'\) and \(\displaystyle Q'\) be the reflection of \(\displaystyle P\) and \(\displaystyle Q\) across \(\displaystyle E\) and \(\displaystyle F\), respectively. Let \(\displaystyle M\) and \(\displaystyle N\) denote the midpoints of line segments \(\displaystyle PB\) and \(\displaystyle QC\), respectively. Prove that \(\displaystyle MN\parallel P'Q'\) and \(\displaystyle P'Q'=2MN\).
Submitted by Van Khea, Cambodia
(5 pont)
 |
Problems with sign 'B'Deadline expired on January 10, 2024. |
B. 5350. \(\displaystyle a)\) Is it possible to find positive integers \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) and \(\displaystyle d\) such that the arithmetic mean of \(\displaystyle a\) and \(\displaystyle b\) is greater than the quadratic mean of \(\displaystyle c\) and \(\displaystyle d\), however, the geometric mean of \(\displaystyle a\) and \(\displaystyle b\) is smaller than the harmonic mean of \(\displaystyle c\) and \(\displaystyle d\)?
\(\displaystyle b)\) Is it possible to find positive integers \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) and \(\displaystyle d\) such that the geometric mean of \(\displaystyle a\) and \(\displaystyle b\) is greater than the quadratic mean of \(\displaystyle c\) and \(\displaystyle d\), however, the arithmetic mean of \(\displaystyle a\) and \(\displaystyle b\) is smaller than the harmonic mean of \(\displaystyle c\) and \(\displaystyle d\)?
Submitted by Bálint Hujter, Budapest
(3 pont)
solution (in Hungarian), statistics
B. 5351. Let \(\displaystyle P\) be an arbitrary point inside the equilateral triangle \(\displaystyle ABC\). The line parallel to \(\displaystyle AB\) through \(\displaystyle P\) intersects sides \(\displaystyle BC\) and \(\displaystyle AC\) in points \(\displaystyle C_1\) and \(\displaystyle C_2\), respectively. Similarly, the parallel through point \(\displaystyle P\) with side \(\displaystyle BC\) intersects sides \(\displaystyle AC\) and \(\displaystyle AB\) in points \(\displaystyle A_1\) and \(\displaystyle A_2\), respectively. Finally, let the parallel through point \(\displaystyle P\) with side \(\displaystyle AC\) intersect sides \(\displaystyle AB\) and \(\displaystyle BC\) in points \(\displaystyle B_1\) and \(\displaystyle B_2\), respectively. Prove that the areas of triangles \(\displaystyle A_1B_1C_1\) and \(\displaystyle A_2B_2C_2\) are equal.
Submitted by Viktor Vígh, Sándorfalva
(3 pont)
solution (in Hungarian), statistics
B. 5352. For which positive integers \(\displaystyle n>3\) is it possible to find \(\displaystyle n\) lines in the plane such that any three of them form an isosceles triangle?
Submitted by Bálint Hujter, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 5353. Prove the following equality for every positive integer \(\displaystyle n>1\):
\(\displaystyle \sum\limits_{i=1}^n\, \sum\limits_{j=1}^n|i-j|=\frac{n(n^2-1)}{3}.\)
Submitted by Mihály Bencze, Brassó
(4 pont)
solution (in Hungarian), statistics
B. 5354. Prove that the Euler line of a scalene triangle is parallel to one of the interior angle bisectors if and only if the bisected angle is \(\displaystyle 120^{\circ}\).
Submitted by Roland Jármai, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 5355. We colored \(\displaystyle n\) squares red in a square lattice. We numbered the red squares from \(\displaystyle 1\) to \(\displaystyle n\), and calculated the sum of the numbers for each pair of squares that share a common side. Is it true that for all arrangements of the \(\displaystyle n\) squares it is possible to number the red squares in a way that we will get a different sum for all pairs that share a common side?
Submitted by András Imolay, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 5356. Prove the following inequality for every integer \(\displaystyle n\geq 2\) and non-negative real numbers \(\displaystyle x_{1},\ldots,x_{n}\):
\(\displaystyle \sqrt[\scriptstyle n]{\prod\limits_{i=1}^{n} (1+x_{i})}\ge 1+\sqrt[\scriptstyle n]{\prod\limits_{i=1}^{n}x_{i}}.\)
Submitted by Ákos Somogyi, London
(6 pont)
solution (in Hungarian), statistics
B. 5357. Let \(\displaystyle ABC\) be a triangle. The tangents at \(\displaystyle B\) and \(\displaystyle C\) to the circumcircle of \(\displaystyle ABC\) intersect at \(\displaystyle P\). Let \(\displaystyle PB\cap AC=D\) and \(\displaystyle PC\cap AB=E\). The perpendicular bisector of the line segment \(\displaystyle BC\) intersects \(\displaystyle AC\) and \(\displaystyle AB\) at \(\displaystyle F\) and \(\displaystyle G\), respectively. The circumcircles of the triangles \(\displaystyle PDF\) and \(\displaystyle PEG\) intersect at \(\displaystyle M\) for the second time. Let \(\displaystyle A'\) be the reflection of \(\displaystyle A\) over \(\displaystyle FG\) and let \(\displaystyle O\) be the circumcenter of the triangle \(\displaystyle AFG\). Prove that the line \(\displaystyle OA'\) passes through one of the intersections of the circles \(\displaystyle MFG\) and \(\displaystyle ADE\).
Submitted by Baris Koyuncu, Istanbul
(6 pont)
 |
Problems with sign 'A'Deadline expired on January 10, 2024. |
A. 866. A graph is called 2-connected, if after deleting any point (and the edges adjacent to it) from the graph it remains still connected.
Is it true that in any 2-connected graph with a countably infinite number of vertices it's always possible to find a trail that is infinite in one direction (i.e. a sequence of not necessarily distinct points \(\displaystyle v_1, v_2,\ldots\) such that \(\displaystyle v_i\) and \(\displaystyle v_{i+1}\) is always connected with an edge, and all edges \(\displaystyle (v_i,v_{i+1})\) are distinct from each other)?
Submitted by Balázs Bursics and Anett Kocsis, Budapest
(7 pont)
A. 867. Let \(\displaystyle p(x)\) be a monic integer polynomial (polynomial with integer coefficients and leading coefficient 1) of degree \(\displaystyle n\) that has \(\displaystyle n\) real roots, \(\displaystyle \alpha_1, \alpha_2,\ldots, \alpha_n\). Let \(\displaystyle q(x)\) be an arbitrary integer polynomial that is relatively prime to polynomial \(\displaystyle p(x)\) (i.e. it's not possible to find an integer polynomial different from constant 1 and \(\displaystyle -1\) that divides both \(\displaystyle p(x)\) and \(\displaystyle q(x)\)). Prove that \(\displaystyle \sum\limits_{i=1}^{n} \big|q(\alpha_i)\big|\ge n\).
Submitted by Dávid Matolcsi, Berkeley
(7 pont)
A. 868. A set of points in the plane is called disharmonic, if the ratio of any two distances between the points is between \(\displaystyle 100/101\) and \(\displaystyle 101/100\), or at least 100 or at most \(\displaystyle 1/100\).
Is it true that for any distinct points \(\displaystyle A_1, A_2,\ldots, A_n\) in the plane it is always possible to find distinct points \(\displaystyle A'_1, A'_2,\ldots,A'_n\) that form a disharmonic set of points, and moreover \(\displaystyle A_i\), \(\displaystyle A_j\) and \(\displaystyle A_k\) are collinear in this order if and only if \(\displaystyle A'_i\), \(\displaystyle A'_j\) and \(\displaystyle A'_k\) are collinear in this order (for all distinct \(\displaystyle 1\le i,j,k\le n\))?
Submitted by Dömötör Pálvölgyi and Balázs Keszegh, Budapest
(7 pont)
Upload your solutions above.
