KöMaL Problems in Mathematics, January 2024
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on February 12, 2024. |
K. 794. We have invested \(\displaystyle 10\,0000\) Euros for one year, 4000 Euros of which for an interest rate of \(\displaystyle 5\%\) per year, and 3500 Euros of which for an interest rate of \(\displaystyle 4\%\) per year. Find the interest rate for the remaining sum, if the total profit of our investment is 500 Euros.
(5 pont)
solution (in Hungarian), statistics
K. 795. The product of four distinct positive prime numbers is \(\displaystyle n\). Find the number of different rectangular prisms that can be created using \(\displaystyle n\) identical little cubes.
(5 pont)
solution (in Hungarian), statistics
K. 796. Which 2D shape has the larger area?
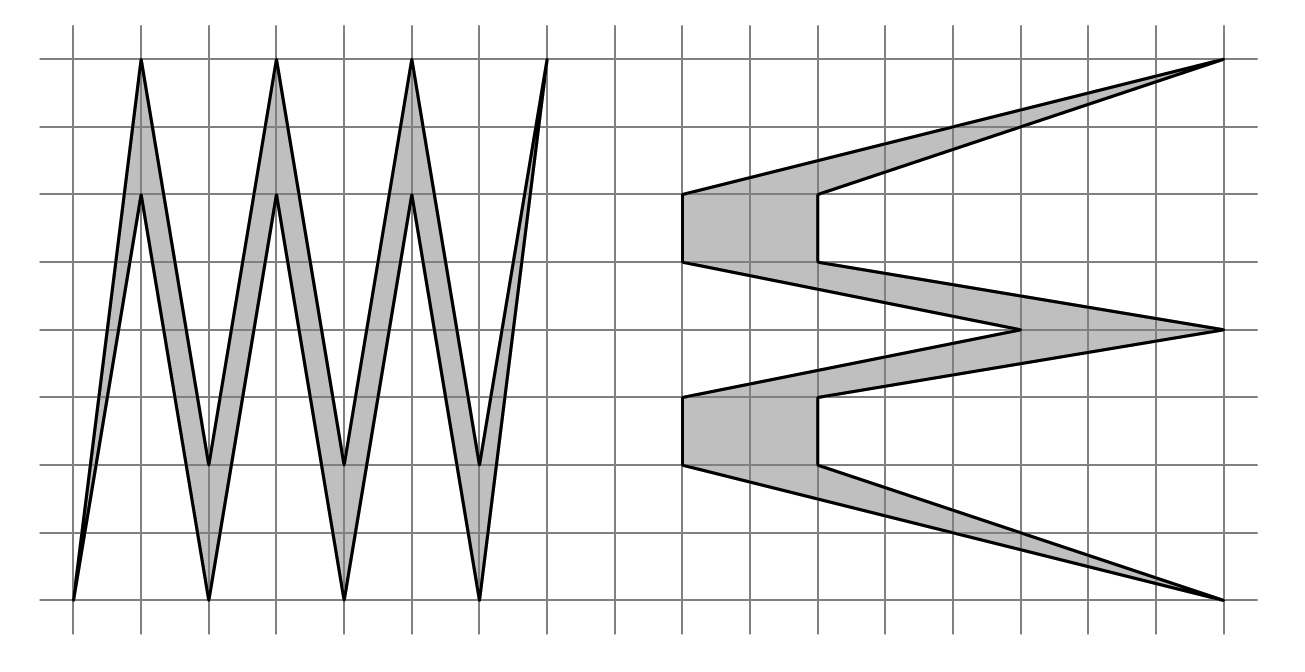
(5 pont)
 |
Problems with sign 'K/C'Deadline expired on February 12, 2024. |
K/C. 797. Let us consider an isosceles right triangle with legs of length 10 cm, and let us draw three circles over the two legs and the hypotenuse as diameters. We colour one of the disks red, the other one blue and the third one green. Find the total area of those parts of the plane which are coloured with at least two colours.
(5 pont)
solution (in Hungarian), statistics
K/C. 798. The main door of the house of the Smiths' is 2 meters high and 1 meters wide. Above the door at the height of 3 meters (measured from the floor) there is a horizontal canopy extending to 1 meter with the shape of a rectangle that has the same width as the door. In the middle of the edge of the canopy that is the furthest away from the door there is a lamp that emits light in all possible directions. Find the area of the part of the floor that is illuminated through the door by the lamp, when the door is completely open. (The ante-room behind the door is wide and long enough so that its floor contains the complete image of the door.)
(5 pont)
 |
Problems with sign 'C'Deadline expired on February 12, 2024. |
C. 1793. Function \(\displaystyle f\) defined on the real numbers satisfies the following two conditions (for all \(\displaystyle x \in \mathbb{R}\)):
| \(\displaystyle (1)\) | \(\displaystyle f(x)=f(147-x),\) |
| \(\displaystyle (2)\) | \(\displaystyle f(x+100)=f(46-x).\) |
Find the value of \(\displaystyle f(200)+f(201)+f(202)\), if we also know that \(\displaystyle f(50)+f(51)+f(52)+f(53)=2024\).
Proposed by Katalin Abigél Kozma, Győr
(5 pont)
solution (in Hungarian), statistics
C. 1794. Circles \(\displaystyle k_1\) and \(\displaystyle k_2\) are externally tangent to each other at point \(\displaystyle A\), circles \(\displaystyle k_2\) and \(\displaystyle k_3\) are externally tangent to each other at point \(\displaystyle B\), and finally circles \(\displaystyle k_1\) and \(\displaystyle k_3\) are externally tangent to each other at point \(\displaystyle C\). Line \(\displaystyle AB\) intersect circle \(\displaystyle k_3\) at point \(\displaystyle D\) (different from \(\displaystyle B\)). Prove that line segments \(\displaystyle AC\) and \(\displaystyle CD\) are perpendicular to each other.
(German competition problem)
(5 pont)
solution (in Hungarian), statistics
C. 1795. Let \(\displaystyle p\) be a real parameter. Find the number of solutions of the following equation as a function of \(\displaystyle p\): \(\displaystyle |x^2-6x+5|=px^2-6px+9p+4\).
Proposed by Gergely Szmerka, Budapest
(5 pont)
solution (in Hungarian), statistics
C. 1796. A regular octahedron with edges of unit length is placed on the plane of one of its triangular face. Find the distance of this plane and the vertices of the octahedron that are not contained in this plane.
Proposed by Bálint Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
C. 1797. Find the largest integer value of \(\displaystyle x\) for which \(\displaystyle x>2\) and the values \(\displaystyle \log_2 (x)\), \(\displaystyle \log_4 (2x)\) and \(\displaystyle \log_8 (3x)\) can be the side lengths of a triangle.
Proposed by Bálint Bíró, Eger
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 12, 2024. |
B. 5358. Find the largest number of distinct positive integers that can be chosen in a way that the sum of any two chosen integers is a perfect power of 2 (with a non-negative exponent).
Proposed by Bálint Hujter, Budapest
(3 pont)
solution (in Hungarian), statistics
B. 5359. \(\displaystyle a)\) Does there exist a triangle such that all of its sides have integer length, and its area is less than \(\displaystyle 1/10\)?
\(\displaystyle b)\) Does there exist a quadrilateral such that all of its sides have integer length, and its area is less than \(\displaystyle 1/10\)?
Proposed by Vígh Viktor, Sándorfalva
(3 pont)
solution (in Hungarian), statistics
B. 5360. The largest angle of scalene triangle \(\displaystyle ABC\) is at vertex \(\displaystyle C\). Let \(\displaystyle T\) denote the foot of altitude from vertex \(\displaystyle C\), and let the angle bisector from vertex \(\displaystyle C\) intersect side \(\displaystyle AB\) at point \(\displaystyle F\). Prove that \(\displaystyle \frac{AT}{TB}=\bigg(\frac{AF}{FB}\bigg)^2\) if and only if \(\displaystyle \angle ACB =90^\circ\).
Based on the idea of Mihály Hujter, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 5361. Let \(\displaystyle a_n\) denote the number of ways \(\displaystyle 2n\) can be obtained as a sum of two positive prime numbers. Is it true that sequence \(\displaystyle (a_n)\) will be monotonically increasing from somewhere?
Proposed by Péter Pál Pach, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 5362. In triangle \(\displaystyle ABC\) it is given that \(\displaystyle \angle BAC=50^\circ\) and \(\displaystyle \angle ABC=70^\circ\). On sides \(\displaystyle AC\) and \(\displaystyle BC\) points \(\displaystyle E\) and \(\displaystyle D\) are chosen satisfying the following properties: \(\displaystyle \angle ABE =\angle BAD = 30^\circ\). Let \(\displaystyle M\) denote the intersection point of line segments \(\displaystyle AD\) and \(\displaystyle BE\). Find the magnitude of angles \(\displaystyle \angle ACM\) and \(\displaystyle \angle BED\).
Proposed by Sándor Róka, Nyíregyháza
(4 pont)
solution (in Hungarian), statistics
B. 5363. Square \(\displaystyle ABCD\) is the base of a right square pyramid, and point \(\displaystyle E\) is its apex. Let \(\displaystyle F\) be the midpoint of lateral edge \(\displaystyle CE\), and let point \(\displaystyle H\) be the trisection point of lateral edge \(\displaystyle BE\) closer to point \(\displaystyle B\). Find the ratio of the volumes of the two parts created by plane \(\displaystyle AHF\) in pyramid \(\displaystyle ABCDE\).
Proposed by Géza Kiss, Csömör
(5 pont)
solution (in Hungarian), statistics
B. 5364. We label the two sides of a coin with integers 1 and 2, and the faces of a cube with integers 1, 2, 3, 4, 5 and 6. Find all weightings of the coin and the cube in a way that tossing both will give the same probabilities for sums 2, \(\displaystyle \ldots\), 8 as two regular tetrahedrons labeled with 1, 2, 3 and 4. (Tossing a tetrahedron will result in the number appearing on the face that rests on the table; and weighting means that the weight distribution of an object can be altered in a way that it will land on its sides with different probabilities.)
Proposed by Mátyás Barczy, Szeged and Gábor Nyul, Debrecen
(6 pont)
solution (in Hungarian), statistics
B. 5365. Find the smallest real number \(\displaystyle \alpha\) for which it is possible to find infinitely many positive integers \(\displaystyle n\) with the property that the difference of \(\displaystyle \sqrt{13}\cdot n\) and the nearest integer is less than \(\displaystyle \alpha /n\).
Proposed by Ákos Somogyi, London
(6 pont)
 |
Problems with sign 'A'Deadline expired on February 12, 2024. |
A. 869. Let \(\displaystyle A\) and \(\displaystyle B\) be given real numbers. Let the sum of real numbers \(\displaystyle 0\le x_1\le x_2\le\dots\le x_n\) be \(\displaystyle A\), and let the sum of real numbers \(\displaystyle 0\le y_1\le y_2\le\dots\le y_n\) be \(\displaystyle B\). Find the largest possible value of \(\displaystyle {\sum_{i=1}^n (x_i-y_i)^2}\).
Proposed by Péter Csikvári, Budapest
(7 pont)
A. 870. We label every edge of a simple graph with the difference of the degrees of its endpoints. If the number of vertices is \(\displaystyle N\), what can be the largest value of the sum of the labels on the edges?
Proposed by Dániel Lenger and Gábor Szűcs, Budapest
(7 pont)
A. 871. Let \(\displaystyle ABC\) be an obtuse triangle, and let \(\displaystyle H\) denote its orthocenter. Let \(\displaystyle \omega_A\) denote the circle with center \(\displaystyle A\) and radius \(\displaystyle AH\). Let \(\displaystyle \omega_B\) and \(\displaystyle \omega_C\) be defined in a similar way. For all points \(\displaystyle X\) in the plane of triangle \(\displaystyle ABC\) let circle \(\displaystyle \Omega(X)\) be defined in the following way (if possible): take the polars of point \(\displaystyle X\) with respect to circles \(\displaystyle \omega_A\), \(\displaystyle \omega_B\) and \(\displaystyle \omega_C\), and let \(\displaystyle \Omega(X)\) be the circumcircle of the triangle defined by these three lines.
With a possible exception of finitely many points find the locus of points \(\displaystyle X\) for which point \(\displaystyle X\) lies on circle \(\displaystyle \Omega(X)\).
Proposed by Vilmos Molnár-Szabó, Budapest
(7 pont)
Upload your solutions above.
