KöMaL Problems in Mathematics, February 2024
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on March 11, 2024. |
K. 799. Misi lives in a street with detached houses only. If we count which house Misi lives in from the beginning of the street on his side, we get twice as many as if we counted which house Misi lives in from the end of the street on the same side. The houses are numbered consecutively from 1 starting at the beginning of the street, with odd numbers on the left and even numbers on the right. Misi's house is on the left side when looking at it from the beginning of the street. Had the houses been numbered from the end, the number of Misi's house would be 25 less than it is now. How many houses are there on that side of the street where Misi lives?
(5 pont)
solution (in Hungarian), statistics
K. 800. The sum of four distinct prime numbers is 50. What can these four primes be?
(5 pont)
solution (in Hungarian), statistics
K. 801. Each of the two pots in the figure below have the shape of a letter. On the other diagram the side view of the pots can be seen, placed before a square lattice with a side length of 10 cm. The pots are open from above, and they spread 10 cm to the back. We place small rubber tubes in each pot that touch the bottom of the pots, and fill them with water. Both pots are filled up at the speed of 1 liter per minute. Find the time required to fill each pot. Plot the graph of the height of the water in each pot as a function of the time elapsed. (Ignore the thickness of the dishes' wall.)
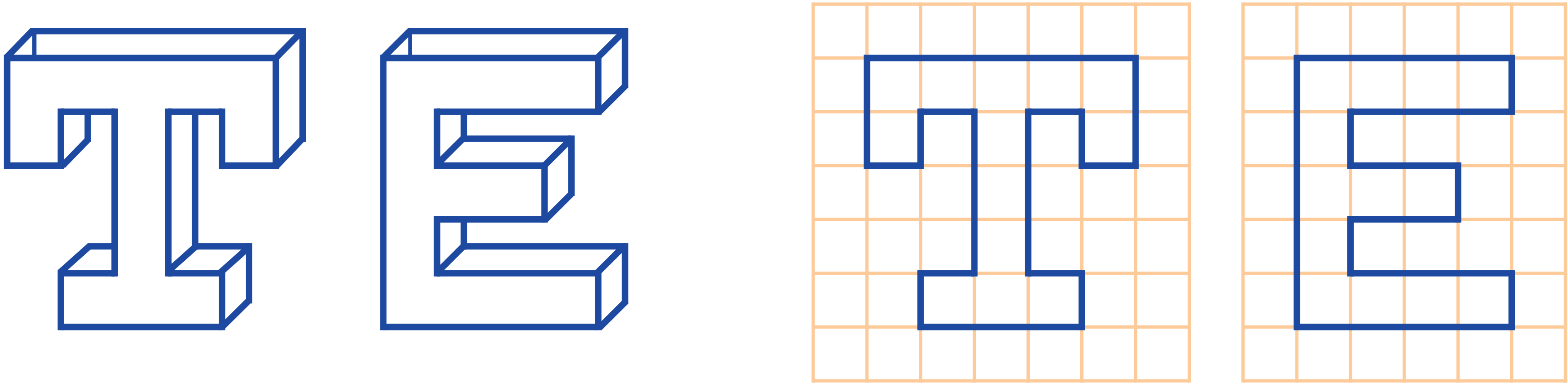
(5 pont)
 |
Problems with sign 'K/C'Deadline expired on March 11, 2024. |
K/C. 802. Let point \(\displaystyle Q\) be an arbitrary inner point of side \(\displaystyle CD\) in square \(\displaystyle ABCD\). Let the perpendicular from vertex \(\displaystyle B\) to line segment \(\displaystyle AQ\) intersect \(\displaystyle AQ\) at \(\displaystyle P\). Let \(\displaystyle K\) denote the intersection point of the diagonals of the square. Prove that line \(\displaystyle PK\) bisects angle \(\displaystyle QPB\).
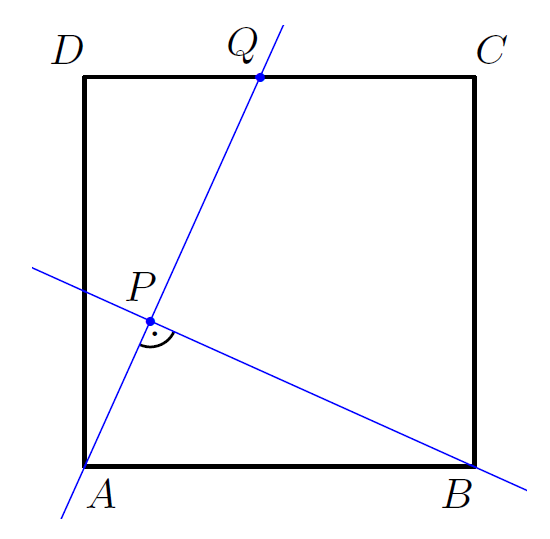
(5 pont)
solution (in Hungarian), statistics
K/C. 803. In a summer camp, all children except for 24 of them are ``only children'' (have no siblings), all children except for 18 have one sibling, and all children except for 14 have two siblings. How many children in this camp can have more than \(\displaystyle 2\) siblings, if we know there is at least one only child, and all the siblings of all the children are also in the camp?
Proposed by Katalin Abigél Kozma, Győr and József Korándi, Budapest
(5 pont)
 |
Problems with sign 'C'Deadline expired on March 11, 2024. |
C. 1798. Let parameter \(\displaystyle p\) be a given integer. Find all integer solutions of the equation \(\displaystyle \big(p+\frac{1}{p}\big)\cdot\big(x-\frac{1}{x}\big)+\big(p-\frac{1}{p}\big)\cdot\big(x+\frac{1}{x}\big)=4px+5+\frac{1}{p}\).
Proposed by Bálint Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
C. 1799. In the unit square \(\displaystyle ABCD\) we draw squares \(\displaystyle DEFG\), \(\displaystyle AHKE\), \(\displaystyle BMFL\) and \(\displaystyle CGNP\) according to the diagram below.
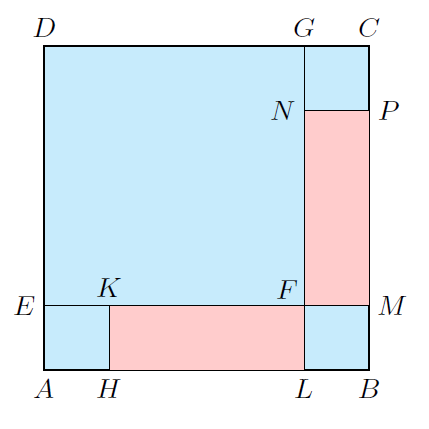
Find the largest possible value of the ratio of the sum of the areas of rectangles \(\displaystyle LFKH\) and \(\displaystyle MPNF\) to the area of square \(\displaystyle ABCD\). Find the exact value of ratio \(\displaystyle \frac{ED}{AD}\) in the extremal case.
Proposed by Bálint Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
C. 1800. Prove that if \(\displaystyle n\) is a natural number, then the interval \(\displaystyle \left[\sqrt{16n+21},\sqrt{16n+24}\right]\) contains no integers.
Proposed by Gábor Holló, Budapest
(5 pont)
solution (in Hungarian), statistics
C. 1801. Let sequence \(\displaystyle a_n\) be defined as \(\displaystyle a_1=2\) and \(\displaystyle a_n=a_{n-1}+2n\). Find the sum of the reciprocals of the first 2024 terms of the sequence (i.e. find the value of \(\displaystyle \frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}+ \dots +\frac{1}{a_{2024}}\)).
Proposed by Gergely Szmerka, Budapest
(5 pont)
solution (in Hungarian), statistics
C. 1802. In regular hexagon \(\displaystyle ABCDEF\) point \(\displaystyle M\) is chosen on diagonal \(\displaystyle AC\) and point \(\displaystyle N\) is chosen on diagonal \(\displaystyle DE\) satisfying \(\displaystyle \frac{AM}{AC}=\frac{CN}{CE}=k\). For which values of \(\displaystyle k\) will points \(\displaystyle B\), \(\displaystyle M\) and \(\displaystyle N\) be collinear?
Matlap, Kolozsvár (2017)
(5 pont)
 |
Problems with sign 'B'Deadline expired on March 11, 2024. |
B. 5366. Is it possible to find a composite number \(\displaystyle n>1\) with the following property: if \(\displaystyle 1=d_1<d_2<\ldots<d_k=n\) denote the positive divisors of \(\displaystyle n\), then \(\displaystyle d_i\) is divisible by \(\displaystyle (d_{i-1} + d_{i-2})\) for all \(\displaystyle 3 \leq i \leq k\)?
(Based on IMO problem 2023/1)
(3 pont)
solution (in Hungarian), statistics
B. 5367. \(\displaystyle a)\) In the open unit disk we place two open line segments of length \(\displaystyle \ell\) with no common points, perpendicularly to each other. What can be the value of \(\displaystyle \ell\)?
\(\displaystyle b)\) In the open unit ball we place three line segments of length \(\displaystyle \ell\) such that any two are disjoint (have no common points) and perpendicular to each other. What can be the value of \(\displaystyle \ell\)?
Proposed by Vígh Viktor, Sándorfalva
(4 pont)
solution (in Hungarian), statistics
B. 5368. In a table tennis championship any two contestants played with each other exactly once. In each match, the winner got 1 point, and the loser got 0 points (there is no tie in table tennis). Interestingly, one contestant has won against exactly those who scored more than him in the championship and lost to exactly those who scored less than him in the championship. Find the smallest possible number of contestants participating in the championship. (It is possible that several contestants got the same score at the end of the championship. At least two contestants participated in the championship.)
Proposed by Kartal Nagy, Budapest and Bálint Hujter, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 5369. Inside an equilateral triangle \(\displaystyle ABC\), point \(\displaystyle P\) is chosen such that \(\displaystyle \angle APB=150^\circ\). Prove that \(\displaystyle {PA^2+PB^2=PC^2}\).
Proposed by Viktor Vígh, Sándorfalva
(4 pont)
solution (in Hungarian), statistics
B. 5370. Let \(\displaystyle k\) be a positive integer, and assume that real numbers \(\displaystyle a_1\), \(\displaystyle \ldots\), \(\displaystyle a_k\) satisfy \(\displaystyle {\sum_{i=1}^k (k-i+1) a_i=0}\). Prove that there exists positive integer \(\displaystyle m\le k\) for which \(\displaystyle 2m\sum_{i=1}^{m} a_i\le \sum_{i=1}^m i a_i\).
Proposed by Viktor Vígh, Sándorfalva
(5 pont)
solution (in Hungarian), statistics
B. 5371. Let point \(\displaystyle P\) be chosen inside triangle \(\displaystyle ABC\). Let \(\displaystyle D\), \(\displaystyle E\) and \(\displaystyle F\) denote the orthogonal projections of point \(\displaystyle P\) onto sides \(\displaystyle BC\), \(\displaystyle CA\) and \(\displaystyle AB\), respectively. Prove that \(\displaystyle \frac{PE+PF}{PA}+\frac{PF+PD}{PB}+\frac{PD+PE}{PC}\le 3\).
Proposed by Mihály Bencze, Brasov
(5 pont)
solution (in Hungarian), statistics
B. 5372. A sphere has been partitioned into spherical triangles and quadrilaterals by drawing some great circles. No three of the great circles pass through the same point, and at least one quadrilateral was created. Prove that there must be exactly eight spherical triangles and six spherical quadrilaterals.
Proposed by Viktor Vígh, Sándorfalva
(6 pont)
solution (in Hungarian), statistics
B. 5373. Let \(\displaystyle n\) be a positive integer. Prove that there are at least 8 odd coefficients in polynomial \(\displaystyle a_{7n}x^{7n}+\dots+a_1x+a_0=(x^7+x^6+x^5+x^4+x^3+x^2+x+1)^n\).
Proposed by Péter Pál Pach, Budapest
(6 pont)
 |
Problems with sign 'A'Deadline expired on March 11, 2024. |
A. 872. For every positive integer \(\displaystyle k\) let \(\displaystyle a_{k,1},a_{k,2},\ldots\) be a sequence of positive integers. For every positive integer \(\displaystyle k\) let sequence \(\displaystyle \{a_{k+1, i}\}\) be the difference sequence of \(\displaystyle \{a_{k, i}\}\), i.e. for all positive integers \(\displaystyle k\) and \(\displaystyle i\) the following holds: \(\displaystyle a_{k, i+1}-a_{k, i}=a_{k+1, i}\). Is it possible that every positive integer appears exactly once among numbers \(\displaystyle a_{k,i}\)?
Proposed by Dávid Matolcsi, Berkeley
(7 pont)
A. 873. Let \(\displaystyle ABCD\) be a convex cyclic quadrilateral satisfying \(\displaystyle AB\cdot CD=AD\cdot BC\). Let the inscribed circle \(\displaystyle \omega\) of triangle \(\displaystyle ABC\) be tangent to sides \(\displaystyle BC\), \(\displaystyle CA\) and \(\displaystyle AB\) at points \(\displaystyle A'\), \(\displaystyle B'\) and \(\displaystyle C'\), respectively. Let point \(\displaystyle K\) be the intersection of line \(\displaystyle ID\) and the nine-point-circle of triangle \(\displaystyle A'B'C'\) that is inside line segment \(\displaystyle ID\). Let \(\displaystyle S\) denote the centroid of triangle \(\displaystyle A'B'C'\). Prove that lines \(\displaystyle SK\) and \(\displaystyle BB'\) intersect each other on circle \(\displaystyle \omega\).
Proposed by Áron Bán-Szabó, Budapest
(7 pont)
A. 874. Nyihaha and Bruhaha are two neighbouring islands, both having \(\displaystyle n\) inhabitants. On island Nyihaha every inhabitant is either a Knight or a Knave. Knights always tell the truth and Knaves always lie. The inhabitants of island Bruhaha are normal people, who can choose to tell the truth or lie. When a visitor arrives on any of the two islands, the following ritual is performed: every inhabitant points randomly to another inhabitant (indepently from each other with uniform distribution), and tells ``He is a Knight'' or ``He is a Knave''. On island Nyihaha, Knights have to tell the truth and Knaves have to lie. On island Bruhaha every inhabitant tells the truth with probability \(\displaystyle 1/2\) independently from each other. Sinbad arrives on island Bruhaha, but he does not know whether he is on island Nyihaha or island Bruhaha. Let \(\displaystyle p_n\) denote the probability that after observing the ritual he can rule out being on island Nyihaha. Is it true that \(\displaystyle p_n \to 1\) if \(\displaystyle n \to \infty\)?
Proposed by Dávid Matolcsi, Berkeley
(7 pont)
Upload your solutions above.
