KöMaL Problems in Physics, March 2024

Problems with sign 'M' Deadline expired on April 15, 2024.

---

M. 430. Fix one end of a wooden skewer such that the skewer is horizontal and start loading the other end. Carry out the measurement with skewers of different lengths. How does the bending of the other end of the skewer depend on the mass of the load and the length of the free part of the skewer? Determine the Young's modulus of the material of the skewer.

(6 pont)

statistics

Problems with sign 'G' Deadline expired on April 15, 2024.

---

G. 845. A car and a lorry leave a crossroad junction at the same time. (The roads are perpendicular to each other.) The car is travelling at a uniform speed of \(\displaystyle 20~\text{m}/\text{s}\) and the truck at \(\displaystyle 15~\text{m}/\text{s}\). After 10 minutes, the truck reaches a crossroad, it turns \(\displaystyle 90^\circ\) and continues travelling at its previous speed on the road. What might the distance between the car and the truck be 20 minutes after they left the junction?

(3 pont)

solution (in Hungarian), statistics

---

G. 846. If we know the size of the Earth's surface, the acceleration due to gravity, and the atmospheric pressure, the total mass of the Earth's atmosphere can be determined with a good approximation. Carry out the calculation. How is it possible that occasionally the air pressure changes significantly, while the mass of the atmosphere remains the same?

(3 pont)

solution (in Hungarian), statistics

---

G. 847. A resistor of resistance \(\displaystyle R_1=1~\text{M}\Omega\) is connected in parallel with another resistor \(\displaystyle R_2\), and then gradually more resistors \(\displaystyle R_3, R_4, \ldots R_n\) are connected in parallel. In each step, the values of the equivalent resistance of the resistors are given as follows:

\(\displaystyle a)\) \(\displaystyle \frac{1}{2}~\text{M}\Omega\), \(\displaystyle \frac{1}{3}~\text{M}\Omega\), \(\displaystyle \frac{1}{4}~\text{M}\Omega\), \(\displaystyle \ldots\), \(\displaystyle \frac{R_1}{n}\);

\(\displaystyle b)\) \(\displaystyle \frac{1}{2}~\text{M}\Omega\), \(\displaystyle \frac{1}{4}~\text{M}\Omega\), \(\displaystyle \frac{1}{8}~\text{M}\Omega\), \(\displaystyle \ldots\), \(\displaystyle \frac{R_1}{2^n}\);

\(\displaystyle c)\) \(\displaystyle \frac{1}{1\cdot2}~\text{M}\Omega\), \(\displaystyle \frac{1}{1\cdot2\cdot3}~\text{M}\Omega\), \(\displaystyle \frac{1}{1\cdot2\cdot3\cdot4}~\text{M}\Omega\), \(\displaystyle \ldots\), \(\displaystyle \frac{R_1}{n!}\).

In each case, what are the resistances of the resistors \(\displaystyle R_2,R_3,~\ldots,R_n\)?

(4 pont)

solution (in Hungarian), statistics

---

G. 848. From the surrounding air a thin beam of light enters to a long, right cylinder, made of some transparent material, at the centre of the base of the cylinder. What can the refractive index of the cylinder's material be in order that the beam of light cannot emerge to the air from the cylinder through the lateral surface of the cylinder?

(4 pont)

solution (in Hungarian), statistics

Problems with sign 'P' Deadline expired on April 15, 2024.

---

P. 5553. A thin disc rotates about an axis, which is perpendicular to the plane of the disc and goes through its centre \(\displaystyle O\), at constant angular acceleration \(\displaystyle \beta\). On the disc, mark a point \(\displaystyle P\) at a distance \(\displaystyle r\) from the centre. How does the magnitude of the acceleration of point \(\displaystyle P\), and the angle between its acceleration vector and the line \(\displaystyle OP\) depend on the distance \(\displaystyle r\)?

(3 pont)

solution (in Hungarian), statistics

---

P. 5554. A glass of base area \(\displaystyle 20~\text{cm}^2\) contains \(\displaystyle 120~\text{g}\) water at a temperature of \(\displaystyle 25~^\circ\text{C}\). Put in an ice cube which has a temperature of \(\displaystyle 0~^\circ\text{C}\). When the ice cube melts completely, the water cools down to exactly \(\displaystyle 0~^\circ\text{C}\). The water equivalent of the glass is \(\displaystyle 40~\text{g}\), i.e. the heat capacity of the glass is equal to that of a sample of \(\displaystyle 40~\text{g}\) water. Ignore other heat losses and the thermal expansion of the glass, but consider the temperature dependence of the density of water.

\(\displaystyle a)\) What was the mass of the ice cube?

\(\displaystyle b)\) How much does the level of the water in the glass change during the melting process of the ice?

(4 pont)

solution (in Hungarian), statistics

---

P. 5555. A disc of radius \(\displaystyle r\) rests on a horizontal, not perfectly smooth tabletop. A larger disc of radius \(\displaystyle R=2r\) slides without rotation along the plane of the tabletop so that its centre moves along a tangent of the small disc. Both discs are made of the same material and have the same height. After the collision, which is considered to be elastic, the large disc slows down due to friction and stops after travelling \(\displaystyle d=5~\text{cm}\). In what direction and how far does the small disc travel on the table? Friction between the discs is negligible.

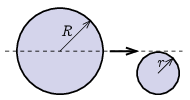
(4 pont)

solution (in Hungarian), statistics

---

P. 5556. On a planet of a distant binary star intelligent creatures are living. Their astronomers have found that the distance between the two stars is constant in time, so they have chosen this distance as the ``astronomical unit'' (AU). Their space scientists have launched a sensitive space telescope to the Lagrangian point of the binary system \(\displaystyle \text{L}_2\), which is located at a distance of \(\displaystyle \tfrac{1}{2}~\text{AU}\) from the lower-mass star, on the opposite side from the other star. What is the ratio of the masses of the two stars?

(5 pont)

solution (in Hungarian), statistics

---

P. 5557. A cylinder of mass \(\displaystyle m\), radius \(\displaystyle r\), and with a uniform mass distribution, rolls back and forth without sliding inside a fixed, thin-walled tube of radius \(\displaystyle R\), near the lowest point of the tube. What is the period of the motion?

(5 pont)

solution (in Hungarian), statistics

---

P. 5558. The radius of the three-quarter circle in the figure is \(\displaystyle R\), the length of the sides of the incomplete square is \(\displaystyle a\). A current of magnitude \(\displaystyle I\) flows in the closed conducting circuit. Find the value of the magnetic induction vector at the centre \(\displaystyle O\) of the circle.

Hint: The value of the magnetic induction at the centre of a square shaped conducting frame of side \(\displaystyle \ell\), through which current \(\displaystyle I\) flows is: \(\displaystyle B=\frac{2\sqrt{2}\mu_0I}{\pi\ell}\).

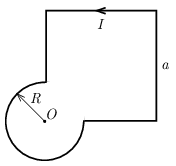
(4 pont)

solution (in Hungarian), statistics

---

P. 5559. A concave and a convex spherical mirror with small aperture (with respect to the radius) and of radius \(\displaystyle R\) are placed at a distance of \(\displaystyle 1.25R\) from each other as shown in the figure.

At which point \(\displaystyle T\) on the common principal axis should a point source of light be placed so that the light rays emitted from it pass through the point \(\displaystyle T\) after reflection in the two mirrors?

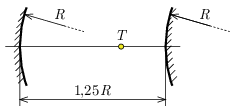
(5 pont)

solution (in Hungarian), statistics

---

P. 5560. On an unknown planet a medium-wave radio station, operating at \(\displaystyle 500~\text{kHz}\), transmits a hum at a frequency of \(\displaystyle 314~\text{Hz}\) in AM modulation. (This frequency has a calming effect on the intelligent creatures of the planet.) A sensitive radio in a spacecraft moving away from the planet at 80% of the speed of light just detects this transmission.

\(\displaystyle a)\) What frequency should the radio receiver be set to?

\(\displaystyle b)\) At what frequency will the astronauts hear the hum?

(5 pont)

solution (in Hungarian), statistics

---

P. 5561. On a stretched string of length \(\displaystyle 2L\), fixed at both ends, with mass \(\displaystyle \mu\) per unit length, the speed of transverse waves is \(\displaystyle c\).

\(\displaystyle a)\) Give the possible frequencies of the eigenvibrations of the string in units \(\displaystyle c/L\).

\(\displaystyle b)\) A point-like body of mass \(\displaystyle M=2\mu L\) is fixed at the centre of the string, as shown in the figure. Write an equation for the possible frequencies of the eigenvibrations of the string and calculate the numerical value of the lowest 3 frequencies in units \(\displaystyle c/L\). The effect of gravity is negligible.

Hint: It can be shown that the forms of the waves can be described by even or odd functions with respect to the centre.

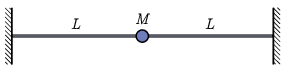
(6 pont)

solution (in Hungarian), statistics