KöMaL Problems in Mathematics, March 2024
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on April 10, 2024. |
K. 804. A football match ended with a score of \(\displaystyle 4:3\) in favor of the home team. Find the number of ways this result could have occured, if it's also given that the away team was leading for a certain period during the match.
(5 pont)
solution (in Hungarian), statistics
K. 805. Let us draw a small equilateral triangle, and let's surround it with identical small triangles in a single layer to form a larger equilateral triangle. Let us also surround this second equilateral triangle with small triangles to form an even larger triangle, and so on. (See figure.)
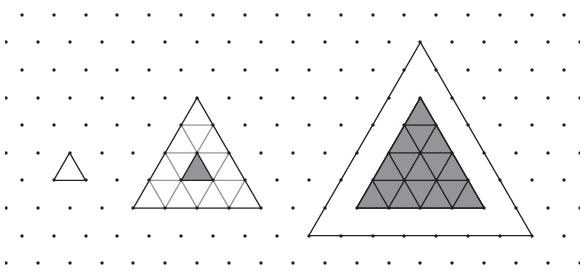
\(\displaystyle a)\) How many small triangles will the twentieth such triangle contain?
\(\displaystyle b)\) How many small triangles will the \(\displaystyle n^{\text{th}}\) such triangle contain?
(5 pont)
solution (in Hungarian), statistics
K. 806. Gizi should have solved inequality \(\displaystyle {\frac{4}{x-2}>5}\), however, she has accidentally replaced 5 with another positive integer. She has solved the modified inequality correctly, and obtained \(\displaystyle 2<x<4\). Find the positive integer that has been written instead of 5 in the inequality.
(5 pont)
 |
Problems with sign 'K/C'Deadline expired on April 10, 2024. |
K/C. 807. How many ways are there to color three squares green in a pink \(\displaystyle 3\times 3\) table, if those colorings that can be reflected or rotated into each other are considered the same?
Proposed by Katalin Fried, Budapest, Korándi József, Budapest
(5 pont)
solution (in Hungarian), statistics
K/C. 808. The square of the sum of a real number and its reciprocal is \(\displaystyle 5\).
\(\displaystyle a)\) Find the sum of the square and the reciprocal of the square of the number without computing the number itself.
\(\displaystyle b)\) Find the sum of the cube and the reciprocal of the cube of the number without computing the number itself.
(5 pont)
 |
Problems with sign 'C'Deadline expired on April 10, 2024. |
C. 1803. Determine the number of triples of positive integers with greatest common divisor \(\displaystyle 4\) and least common multiple 2024.
Proposed by Katalin Abigél Kozma, Győr
(5 pont)
solution (in Hungarian), statistics
C. 1804. In triangle \(\displaystyle ABC\) let \(\displaystyle D\), \(\displaystyle E\) and \(\displaystyle F\) denote the midpoints of the sides \(\displaystyle BC\), \(\displaystyle CA\) and \(\displaystyle AB\), respectively. Let \(\displaystyle K_a\), \(\displaystyle K_b\) and \(\displaystyle K_c\) denote the centers of the incircles of triangles \(\displaystyle AFE\), \(\displaystyle BDF\) and \(\displaystyle CED\), respectively. Prove that the sum of the areas of quadrilaterals \(\displaystyle K_aFDE\), \(\displaystyle K_bDEF\) and \(\displaystyle K_cEFD\) equals the area of triangle \(\displaystyle ABC\).
Proposed by Bálint Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
C. 1805. Solve equation \(\displaystyle {\frac{6x-3}{3x}-\Big(3y^2-14xy+8x\Big)^2=x}\) for positive real numbers \(\displaystyle x\) and \(\displaystyle y\).
Proposed by Bálint Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
C. 1806. The login to a banking application on a smartphone requires a four-digit PIN code. For security reasons, the digits appear randomly at the keypad locations shown in the diagram such that the probability of each possible distribution is the same. (One possible distribution is shown in the diagram.) If our PIN code consists of four different digits, what is the probability that we leave fingerprints at the same locations during two logins?

Proposed by Merse Előd Gáspár, Budapest
(5 pont)
solution (in Hungarian), statistics
C. 1807. In triangle \(\displaystyle ABC\) angles satisfy \(\displaystyle 2\beta = 3\gamma\). Let points \(\displaystyle D\) and \(\displaystyle E\) be chosen on side \(\displaystyle AC\) such that \(\displaystyle BD\) and \(\displaystyle BE\) trisect angle \(\displaystyle \beta\), and point \(\displaystyle D\) is located between points \(\displaystyle A\) and \(\displaystyle E\). Further, let \(\displaystyle F\) denote the intersection of side \(\displaystyle AB\) and the angle bisector of \(\displaystyle \gamma\). Prove that \(\displaystyle BE\) and \(\displaystyle DF\) are parallel.
(Swiss competition problem)
(5 pont)
 |
Problems with sign 'B'Deadline expired on April 10, 2024. |
B. 5374. Square \(\displaystyle ABCD\) and rhombus \(\displaystyle BAEF\) are drawn on the opposite sides of line segment \(\displaystyle AB\). Let \(\displaystyle K\) and \(\displaystyle M\) denote the center of the square and the rhombus, respectively. Prove that \(\displaystyle KM\) bisects angle \(\displaystyle AMB\).
Proposed by Viktor Vígh, Sándorfalva
(3 pont)
solution (in Hungarian), statistics
B. 5375. Solve equation \(\displaystyle \left(m-k \right)^{2}={m+k}\) for non-negative integers \(\displaystyle m\) and \(\displaystyle k\).
Proposed by László Németh, Fonyód
(4 pont)
solution (in Hungarian), statistics
B. 5376. Let us divide positive integer \(\displaystyle n\) with all the positive integers smaller than \(\displaystyle n\), and let \(\displaystyle f(n)\) denote the sum of the remainders we've obtained. (For example, when we divide \(\displaystyle n=5\) by \(\displaystyle 1\), \(\displaystyle 2\), \(\displaystyle 3\) and \(\displaystyle 4\), we get remainders \(\displaystyle 0\), \(\displaystyle 1\), \(\displaystyle 2\) and \(\displaystyle 1\), respectively, therefore \(\displaystyle f(5)=4\).) Solve equation \(\displaystyle f(n)=n\).
Proposed by Attila Sztranyák, Budapest
(4 pont)
B. 5377. Determine the set of real numbers \(\displaystyle p\) satisfying the following property: inequality \(\displaystyle \sqrt{a^2+b^2-ab}+\sqrt{b^2+c^2-bc}\geq \sqrt{a^2+c^2-p\cdot ac}\) holds for all triples of positive real numbers \(\displaystyle a\), \(\displaystyle b\) and \(\displaystyle c\), for which the square roots are defined.
Proposed by Zoltán Lóránt Nagy, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 5378. Let \(\displaystyle n\) and \(\displaystyle k\) be positive integers. Prove that if \(\displaystyle n \leq k^{11}\), then \(\displaystyle n\) can be obtained as the product of ten positive integers, among which no composite number greater than \(\displaystyle k^2\) appears.
Proposed by Péter Pál Pach, Budapest
(5 pont)
B. 5379. Let \(\displaystyle ABC\) be a triangle with a right angle at \(\displaystyle C\). On the hypotenuse \(\displaystyle AB\), let \(\displaystyle H\) and \(\displaystyle D\) be the feet of the altitude and the angle bisector starting from \(\displaystyle C\), respectively. The bisector of angle \(\displaystyle AHC\) meets \(\displaystyle AC\) at point \(\displaystyle E\), and the bisector of angle \(\displaystyle CHB\) meets \(\displaystyle BC\) at \(\displaystyle F\). Mark a point \(\displaystyle M\) on line segment \(\displaystyle HE\) and a point \(\displaystyle N\) on line segment \(\displaystyle HF\) that satisfy \(\displaystyle HM:HE=HN:HF\). Show that lines \(\displaystyle CD\), \(\displaystyle AM\) and \(\displaystyle BN\) are concurrent.
Proposed by Nguyen Duy Khanh, Vietnam
(5 pont)
solution (in Hungarian), statistics
B. 5380. Find the smallest possible degree of polynomial \(\displaystyle f\) of one variable, if it satisfies the following property: the range of \(\displaystyle f\) and \(\displaystyle f\circ f\) are different, while the range of \(\displaystyle f \circ f\) and \(\displaystyle f\circ f\circ f\) are the same. (The symbol \(\displaystyle \circ\) denotes function composition.)
Proposed by Bálint Hujter, Budapest
(6 pont)
solution (in Hungarian), statistics
B. 5381. Let \(\displaystyle ABCDEFGH\) be a cyclic octagon inscribed in circle \(\displaystyle \Omega_1\) and let \(\displaystyle \Omega_2\) be another circle inside \(\displaystyle \Omega_1\). Assume that circles \(\displaystyle \omega_1\), \(\displaystyle \omega_2\), \(\displaystyle \omega_3\), \(\displaystyle \omega_4\) are tangent to \(\displaystyle \Omega_2\) externally; moreover, \(\displaystyle \omega_1\) is tangent to arc \(\displaystyle AB\) of \(\displaystyle \Omega_1\) internally, and tangent to line segments \(\displaystyle AF\) and \(\displaystyle BE\); \(\displaystyle \omega_2\) is tangent to arc \(\displaystyle CD\) internally, and tangent to \(\displaystyle CH\) and \(\displaystyle DG\); \(\displaystyle \omega_3\) is tangent to arc \(\displaystyle EF\) internally, and tangent to \(\displaystyle AF\) and \(\displaystyle BE\); finally, \(\displaystyle \omega_4\) is tangent to arc \(\displaystyle GH\) internally, and tangent to \(\displaystyle CH\) and \(\displaystyle DG\), as shown in the figure. Prove that the quadrilateral enclosed by segments \(\displaystyle AF\), \(\displaystyle BE\), \(\displaystyle CH\) and \(\displaystyle DG\) has an inscribed circle.
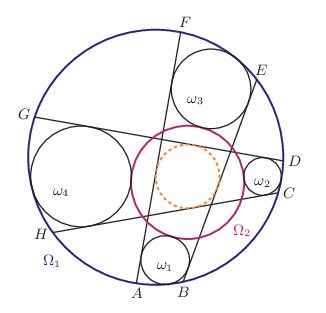
Proposed by Géza Kós, Budapest
(6 pont)
 |
Problems with sign 'A'Deadline expired on April 10, 2024. |
A. 875. \(\displaystyle a)\) Two players play a cooperative game. They can discuss a strategy prior to the game, however, they cannot communicate and have no information about the other player during the game. The game master chooses one of the players in each round. The player on turn has to guess the number of the current round. Players keep note of the number of rounds they were chosen, however, they have no information about the other player's rounds. If the player's guess is correct, the players are awarded a point. Player's are not notified whether they've scored or not. The players win the game upon collecting 100 points. Does there exist a strategy with which they can surely win the game in a finite number of rounds?
\(\displaystyle b)\) How does this game change, if in each round the player on turn has two guesses instead of one, and they are awarded a point if one of the guesses is correct (while keeping all the other rules of the game the same)?
Proposed by Gábor Szűcs, Budapest
(7 pont)
A. 876. Find all non-negative integers \(\displaystyle a\) and \(\displaystyle b\) satisfying \(\displaystyle 5^a+6=31^b\).
Proposed by Erik Füredi, Budapest
(7 pont)
A. 877. Convex quadrilateral \(\displaystyle ABCD\) is circumscribed about circle \(\displaystyle \omega\). A tangent to \(\displaystyle \omega\) parallel to diagonal \(\displaystyle AC\) meets diagonal \(\displaystyle BD\) at point \(\displaystyle P\) outside of \(\displaystyle \omega\). The second tangent from \(\displaystyle P\) to \(\displaystyle \omega\) touches \(\displaystyle \omega\) at point \(\displaystyle T\). Prove that \(\displaystyle \omega\) and the circumcircle of triangle \(\displaystyle ATC\) are tangent.
Proposed by Nikolai Beluhov, Bulgaria
(7 pont)
Upload your solutions above.
