KöMaL Problems in Mathematics, April 2024

Problems with sign 'K' The deadline is: May 10, 2024 24:00 (UTC+02:00).

K. 809. Let \(\displaystyle a_1\) be a positive integer from which we create a sequence according to the following rule. If the decimal form of \(\displaystyle a_n\) is \(\displaystyle 10A_n+b_n\) (where \(\displaystyle b_n\) is the unit digit of \(\displaystyle a_n\)), then \(\displaystyle a_{n+1}=A_n+6b_n\). Show that either all terms of the sequence are divisible by \(\displaystyle 59\) or none of them are.

János Urbán (1939–2012), Budapest

(5 pont)

This problem is for grade 9 students only.

K. 810. Trapezoid \(\displaystyle ABCD\) has the following properties: \(\displaystyle AB\parallel CD\), \(\displaystyle AB=3CD\) and \(\displaystyle CD=DA\). Find the angles of the trapezoid knowing that \(\displaystyle \angle CDA=120^{\circ}\).

German competition problem

(5 pont)

This problem is for grade 9 students only.

K. 811. We have filled in the squares of the \(\displaystyle 8\times 8\) chessboard with the positive integers from \(\displaystyle 1\) to \(\displaystyle 64\) in increasing order, starting from the top left corner and proceeding row by row. Is it possible to delete two numbers from two adjacent squares (two squares sharing an edge or a vertex) such that the sum of the remaining numbers is exactly \(\displaystyle 2024\)?

Proposed by Bálint Bíró, Eger

(5 pont)

This problem is for grade 9 students only.

Problems with sign 'K/C' The deadline is: May 10, 2024 24:00 (UTC+02:00).

K/C. 812. Number \(\displaystyle 2024\) has the property that exactly one of its digits (namely the 0) is a multiple of its every other digit. How many four-digit positive integers have at least two such digits?

Proposed by Katalin Abigél Kozma, Győr

(5 pont)

This problem is for grades 1–10 students only.

K/C. 813. We draw square \(\displaystyle EBFG\) and several other squares congruent to it next to square \(\displaystyle ABCD\) according to the diagram. Find the ratio of the areas of triangle \(\displaystyle DHE\) and quadrilateral \(\displaystyle HKLE\).

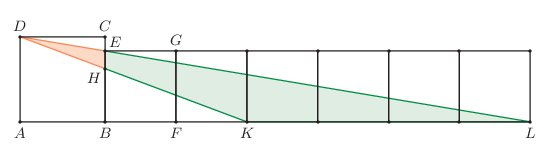
Based on the idea of János Deres, Csurgó

(5 pont)

This problem is for grades 1–10 students only.

Problems with sign 'C' The deadline is: May 10, 2024 24:00 (UTC+02:00).

C. 1808. Boglárka fills in each square of a \(\displaystyle 4\times 4\) lattice with exactly one of numbers \(\displaystyle 2023\), \(\displaystyle 2024\) and \(\displaystyle 2025\). How many ways can she do this, if we also require that the sum of the four numbers in each row and each column must be divisible by 3?

Proposed by Katalin Abigél Kozma, Győr

(5 pont)

C. 1809. Let point \(\displaystyle B\) be chosen inside line segment \(\displaystyle AC\). We draw isosceles triangles \(\displaystyle ABS_1\), \(\displaystyle BCS_2\) and \(\displaystyle CAS_3\) with no common interior points, bases \(\displaystyle AB\), \(\displaystyle BC\) and \(\displaystyle CA\), respectively, and base angles of \(\displaystyle 30^{\circ}\). Prove that triangle \(\displaystyle S_1S_2S_3\) is equilateral.

German competition problem

(5 pont)

C. 1810. Find the real roots of equation \(\displaystyle (x+2)^6+(x^2-4x-4)^3=8x^6\).

Proposed by Bálint Bíró, Eger

(5 pont)

C. 1811. Let \(\displaystyle f(x)=x^2\) and \(\displaystyle g(x)=x^2-2x+2\). Find the equation of the common tangent of the graphs of these two functions.

Proposed by Csaba Sándor, Budapest

(5 pont)

This problem is for grades 11–12 students only.

C. 1812. Let \(\displaystyle a\), \(\displaystyle b\) and \(\displaystyle c\) denote the lengths of the sides of a triangle satisfying \(\displaystyle a+b=3c\). Let \(\displaystyle \alpha\) and \(\displaystyle \beta\) denote the angles opposite to sides \(\displaystyle a\) and \(\displaystyle b\), respectively. Prove that \(\displaystyle \cot{\frac{\alpha}{2}}\cdot{\cot{\frac{\beta}{2}}}=2\).

Croatian competition problem

(5 pont)

This problem is for grades 11–12 students only.

Problems with sign 'B' The deadline is: May 10, 2024 24:00 (UTC+02:00).

B. 5382. Do there exist prime numbers \(\displaystyle 2<p<q\) for which more than one third of the elements of set \(\displaystyle \{ p+1, p+2, \ldots, q-1 \}\) is a prime number?

Proposed by Bálint Hujter, Budapest

(3 pont)

B. 5383. Cyclic quadrilateral \(\displaystyle ABCD\) has the following properties: \(\displaystyle \angle BAD = 90^{\circ}\), \(\displaystyle BC = CD\) and \(\displaystyle AC = 1\). Find the area of \(\displaystyle ABCD\).

Proposed by Mihály Hujter, Budapest

(3 pont)

B. 5384. Prove that if \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c>0\) and \(\displaystyle a^2+b^2+c^2=abc\), then \(\displaystyle 2(a+b+c)+\frac{a^3}{bc}+\frac{b^3}{ca}+\frac{c^3}{ab} \le abc\).

Proposed by Mihály Bencze, Brasov

(4 pont)

B. 5385. Let \(\displaystyle F\) denote the center of the nine-point circle of acute triangle \(\displaystyle ABC\). Prove that \(\displaystyle AF^2-BF^2=Rc\sin(\beta-\alpha)\), where \(\displaystyle R\) denotes the radius of the circumcircle, \(\displaystyle c\) denotes the length of side \(\displaystyle AB\), and \(\displaystyle \alpha\) and \(\displaystyle \beta\) denote the interior angles at \(\displaystyle A\) and \(\displaystyle B\).

Proposed by Mihály Bencze, Brasov

(4 pont)

B. 5386. Anna and Balázs play the following game: Anna tosses a fair coin 101 times, and Balázs tosses a fair coin 10 times. Anna wins, if she receives more than ten times as many heads as Balázs, otherwise Balázs wins. Find the player to whom this game is favorable.

Proposed by: Attila Sztranyák, Budapest

(5 pont)

B. 5387. We have colored finitely many points on the plane to red, blue or green such that no three points of the same color are collinear, however, any line segment connecting two points with the same color contains a third colored point (with a different color). Find the maximum number of the colored points.

Proposed by Sándor Róka, Nyíregyháza

(5 pont)

B. 5388. Prove that any \(\displaystyle 2n\) consecutive positive integers can be divided into \(\displaystyle n\) pairs in at least \(\displaystyle n!\) different ways such that in each pair the product of the two numbers is not a perfect square.

Proposed by Sándor Róka, Nyíregyháza

(6 pont)

B. 5389. Let \(\displaystyle I\) denote the incenter of acute triangle \(\displaystyle ABC\). Let the incircle touch sides \(\displaystyle BC\) and \(\displaystyle AC\) at points \(\displaystyle D\) and \(\displaystyle E\), respectively. Let \(\displaystyle H\) denote the orthocenter of triangle \(\displaystyle ABC\). Prove that if \(\displaystyle H\) is on line segment \(\displaystyle DE\), then line \(\displaystyle HI\) bisects side \(\displaystyle AB\).

Proposed by Boldizsár Varga, Budapest

(6 pont)

Problems with sign 'A' The deadline is: May 10, 2024 24:00 (UTC+02:00).

A. 878. Let point \(\displaystyle A\) be one of the intersections of circles \(\displaystyle c\) and \(\displaystyle k\). Let \(\displaystyle X_1\) and \(\displaystyle X_2\) be arbitrary points on circle \(\displaystyle c\). Let \(\displaystyle Y_i\) denote the intersection of line \(\displaystyle AX_i\) and circle \(\displaystyle k\) for \(\displaystyle i=1,2\). Let \(\displaystyle P_1\), \(\displaystyle P_2\) and \(\displaystyle P_3\) be arbitrary points on circle \(\displaystyle k\), and let \(\displaystyle O\) denote the center of circle \(\displaystyle k\). Let \(\displaystyle K_{ij}\) denote the center of circle \(\displaystyle (X_iY_iP_j)\) for \(\displaystyle i=1,2\) and \(\displaystyle j=1,2,3\). Let \(\displaystyle L_j\) denote the center of circle \(\displaystyle (OK_{1j}K_{2j})\) for \(\displaystyle j=1,2,3\). Prove that points \(\displaystyle L_1\), \(\displaystyle L_2\) and \(\displaystyle L_3\) are collinear.

Proposed by Vilmos Molnár-Szabó, Budapest

(7 pont)

A. 879. An integer \(\displaystyle k>2\) is given. Xavier and Yvette play the following game: a number \(\displaystyle n>k\) is initially written on the blackboard. The two players take turns, Xavier starts. In each turn the integer \(\displaystyle m\) on the blackboard is replaced by integer \(\displaystyle m'\) satisfying \(\displaystyle k\le m'<m\) and \(\displaystyle \gcd (m,m')=1\). The player who cannot make a legal move loses the game. We say that integer \(\displaystyle n>k\) is good if Yvette has a winning strategy. Prove that if \(\displaystyle n\), \(\displaystyle n'>k\) are two integers satisfying the condition that every prime \(\displaystyle p\le k\) divides \(\displaystyle n\) if and only if it divides \(\displaystyle n'\), then \(\displaystyle n\) is good if and only if \(\displaystyle n'\) is good.

(7 pont)

A. 880. Find all triples \(\displaystyle (a,b,c)\) of real numbers for which there exists a function \(\displaystyle f\colon \mathbb{Z}^+ \to \mathbb{Z}^+\) satisfying \(\displaystyle af(n)+bf(n+1)+cf(n+2)<0\) for every \(\displaystyle n \in \mathbb{Z}^+\) (\(\displaystyle \mathbb{Z}^{+}\) denotes the set of positive integers).

Proposed by András Imolay, Budapest

(7 pont)