English Issue, December 2002
	Previous page	Contents	Next page	ORDER FORM

Problems in information technology
(34-36.)

I. 34. Binomial coefficients can be used to represent natural numbers in the so-called binomial base. For a fixed m (2$\displaystyle \le$m $\displaystyle \le$50) every natural number n (0$\displaystyle \le$n$\displaystyle \le$10000) can uniquely be represented as

$\displaystyle n={a_1\choose1}+{a_2\choose2}+\cdots+ {a_m\choose m}$, where 0$\displaystyle \le$a₁<a₂<...<a_m.

Your program (I34.pas, ...) should read the numbers n and m, then display the corresponding sequence a₁,a₂,...,a_m.

Example. Let n=41, then a₁=1, a₂=2, a₃=4, a₄=7, because

$\displaystyle 41={1\choose1}+{2\choose2}+{4\choose3}+{7\choose4}=1+ 1+4+35.$

(10 points)

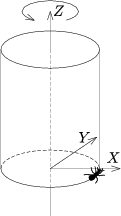
I. 35. We put an ant close beside the base of a cylinder-jacket with radius R and height H. In every minute the ant creeps upwards M centimetres. The cylinder is rotated around its axis (which is just the Z-axis) anticlockwise completing T turns per minute. The ant starts from the point (R,0,0), and we are watching it at an angle of ALPHA degree relative to the Y-axis, see Figure 1.

Figure 1	Figure 2

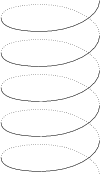
Write your program (I35.pas, ...) which reads the values of R (1$\displaystyle \le$R$\displaystyle \le$50), H (1$\displaystyle \le$H$\displaystyle \le$200), M (1$\displaystyle \le$M$\displaystyle \le$H), T (1$\displaystyle \le$T$\displaystyle \le$100) and ALPHA (0$\displaystyle \le$ALPHA<90), then displays the axonometric projection to the plane Y=0 of the path of the ant using continuous line on the visible side of the cylinder and dotted line on the back side.

Example. Figure 2 shows the path of the ant with R=50, H=200, M=1, T=40, ALPHA=30.

(10 points)

I. 36. According to the trinomial theorem

$\displaystyle {(x+y+z)}^n=\sum_{\textstyle{0\le a,b,c\le n\atop a+b+c=n}} {a+b+c\choose a,b,c}x^ay^bz^c.$

The trinomial coefficients can be computed, for example, by the formula

$\displaystyle {a+b+c\choose a,b,c}=\frac{(a+b+c)!}{a!b!c!}.$

However, these factorials can be very large, thus their direct computation is not always feasible. Nevertheless, writing trinomial coefficients as a product of binomial coefficients can settle this problem.

Prepare your sheet (I36.xls) which, if n (n=a+b+c, n$\displaystyle \le$20) is entered into a given cell, displays a table of trinomial coefficients, similar to the one below.

The example shows the coefficients when n=5.

(10 points)