 | English Issue, December 2002 | |||
| Previous page | Contents | Next page | ORDER FORM | |
Solutions of advanced problems A
A. 269. A circular hole is to be completely covered with two square boards. The sides of the squares are 1 metre. In what interval may the diameter of the hole vary?

Figure 1
It is easy to see that a hole of radius 2−√2 (and all smaller holes) can be covered by two unit squares, see Figure 1.
We will prove that if a unit square covers at least half of the perimeter of a circle of radius r, then r≤2−√2. This implies that the diameter of the hole cannot exceed
4−2√2≈1.17 metre.
Let K be a circle of radius r, and N be a unit square, which covers at least the half of K. If r≥1/2, then N can be translated such that each side of N or its extension has at least one common point with K and the covered part of the curve is increasing, see Figure 2.

Figure 2
So, it can be assumed that r>1/2 and (the extension of) each side of N has a common point with K.
First, assume that a vertex of N is inside K. Let the vertices of N be A, B, C, D and suppose that A is inside K. Denote the intersection of K and the half-lines AB and AD by P and Q, respectively. (Figure 3.)
Because PAQ∠=90o, the centre of K and vertex A are on the same side of line PQ. This implies that the uncovered arc PQ is longer than the half of K. This is a contradiction, thus this case is impossible.
We are left to deal with the case when there are no vertices of N inside K and each side or its extension has a common point with K. It is easy to check that these common points cannot be on the extension of the sides of N; they must lie on the perimeter of N.
 |  |
| Figure 3 | Figure 4 |
Denote by α, β, γ and δ the angles drawn on Figure 4.
The total of the uncovered arcs is at most the half of K, so α+β+γ+δ 90o. By symmetry, it can be assumed that
90o. By symmetry, it can be assumed that  +
+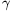
 45o.
45o.
As can be read from the Figure, r(cos  +cos
+cos 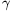 )=r(cos
)=r(cos 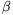 +cos
+cos 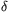 )=1. The concavity of the cosine function yields
)=1. The concavity of the cosine function yields
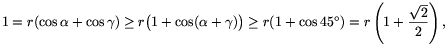
and hence 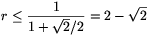 .
.
Thus, the radius of the hole can be at most 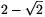 ; its diameter can be at most
; its diameter can be at most 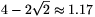 metre.
metre.
