Solutions for advanced problems "A" in February, 2002

In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.

A. 284. Let f be a function defined on the subsets of a finite set S. Prove that if f(S\A)=f(A) and max(f(A),f(B))$\displaystyle ge$f(A$\displaystyle cup$B) for all subsets A, B of S, then f assumes at most |S| distinct values.

(Miklós Schweitzer Memorial Competition, 2001)

Solution 1. In the case of S=$\displaystyle emptyset$, the statement is not true. Assume from now on that S is not empty.

The proof is by induction. For |S|=1 and |S|=2 the number of complementary pairs of subsets is exactly 1 and 2, respectively, thus the function can have no other values. Now let |S|>2, and assume that the statement is true for smaller numbers of elements.

Let the m be the largest value of f. First prove that S has a one-element subset X={x}, such that f(X)=m. Consider the subsets assigned the number m by the function f. It follows from the complementary property that there is a nonempty set among these subsets. Thus consider the smallest nonempty subset X, such that f(X)=m. If X had at least two elements, it could be expressed as the union of two smaller sets: X=X₁$\displaystyle cup$X₂, but then, as max(f(X₁),f(X₂))$\displaystyle ge$f(X₁$\displaystyle cup$X₂)=f(X)=m, one of f(X₁) and f(X₂) would also be m. Therefore, the set X has one element.

Let R=S\X, and define the function g:P(R)$\displaystyle to$R as follows: for all A$\displaystyle subset$R, let

g(A)=min(f(A),f(A$\displaystyle cup$X))=min(f(A),f(R\A)).

Note that for any A$\displaystyle subset$R, max(f(A),f(A$\displaystyle cup$X))=m, as

m=f(X)=f(S\X)=f(A$\displaystyle cup$(R\A))$\displaystyle le$max(f(A),f(R\A))=

=max(f(A),f(S$R\A)))=max(f(A),f(A\(\displaystyle cup$X)).

There remains to prove that the assumption of the induction is true for the function g, that is, g(R\A)=g(A) és g(A$\displaystyle cup$B)$\displaystyle le$max(g(A),g(B)) for all A,B$\displaystyle subset$R. Then, according to the assumption, g may have at most (|S|-1) different values. For any set A$\displaystyle subset$T, one of f(A) and f(A+X) is m, and the other is g(A). Hence the range of f can only be wider than the range of g by the single element m.

The property g(R\A)=g(A) can be derived fom the definition of g.

If either of g(A) or g(B) is m, then g(A$\displaystyle cup$B)$\displaystyle le$max(g(A),g(B)) follows trivially. Assume, therefore, that g(A) and g(B) are smaller than m, that is, one of f(A) and f(A$\displaystyle cup$X), and one of f(B) and f(B$\displaystyle cup$X) are smaller than m-nél. If f(A)<m, then let C=A, otherwise let C=A$\displaystyle cup$X. Similarly, for f(B)<m let D=B, otherwise D=B$\displaystyle cup$X. Then f(C)=g(A) and f(D)=g(B), and the set C$\displaystyle cup$D is either A$\displaystyle cup$B or A$\displaystyle cup$B$\displaystyle cup$X. Therefore,

max(g(A),g(B))=max(f(C),f(D))$\displaystyle ge$f(C$\displaystyle cup$D)$\displaystyle ge$

$\displaystyle ge$min(f(A$\displaystyle cup$B),f(A$\displaystyle cup$B$\displaystyle cup$X))=g(A$\displaystyle cup$B).

Thus the function g satisfies the requirements.

Solution 2. (by E. Csóka). The solution is based on the following lemma:

Lemma. For a real number v, let S_v be the set of those subsets of the set S for which the value assigned by the function f is not greater than v:

S_v={X$\displaystyle subset$S: f(X)$\displaystyle le$v}.

Then |S_v| is either 0, or a power of 2 that is different from 1.

Proof for the lemma. First observe that S_v is closed for complement, union, intersection and difference, that is, for all sets X,Y in S_v, S\X, X$\displaystyle cap$Y, X$\displaystyle cup$Y and X\Y are also in S_v. The first two are true because f(S\X)=f(X)$\displaystyle le$v, and f(X$\displaystyle cup$Y)$\displaystyle le$max(f(X),f(Y))$\displaystyle le$max(v,v)=v; and both intersection and difference can be expresssed in terms of complement and union.

It follows from the closure for union and complement that if S_v is not empty, then S$\displaystyle in$S_v.

It follows from the closure for complement that if S_v has at least one element then the complement of that element is also an element. Thus the elements of S_v can be paired up, and therefore S_v cannot be a one-element set.

Let the atoms of S_v be its nonempty subsets with the minimum number of elements. Thus a nonempty set A$\displaystyle in$S_v is an atom if and only if for all X$\displaystyle subset$A, X$\displaystyle in$S_v it is true that X=$\displaystyle emptyset$ or X=A.

Two important things follow from the definition of atoms. One of them is that if A$\displaystyle in$S_v is an atom and X$\displaystyle in$S_v is an arbitrary set, then A is a subset of either X or (S\X). If it were not, A\X would not be the empty set but a proper subset of A, which contradicts to A being an atom. The other important consequence is that atoms are pairwise disjoint. If there were two non-disjoint atoms, then they would contain each other for the above reason, that is, the two atoms would be identical.

Now we shall prove that every element of the set S is contained in exactly one atom of S_v. As the atoms are pairwise disjoint, x can belong to at most one atom, and all we need to prove is that such an atom exists. Let x$\displaystyle in$S be an arbitrary element. Consider a set in S_v that contains x and has the minimum number of elements, and call it A. If A is not an atom then it is not minimal, that is, it has a subset X$\displaystyle subset$A that is not empty but not equal to A either. Then X and A\X are both in S_v, they are proper subsets of A, and one of them contains x. This contradicts to A being minimal among the sets in S_v containing x. Therefore, A is an atom.

It follows that any set in X$\displaystyle in$S_v can be expressed in one unique way as the union of atoms in S_v. For any element x$\displaystyle in$S, let A_x be the atom for which x$\displaystyle in$A_x. The unique representation of the set X is as follows:

$\displaystyle X=\bigcup_{x\in X}A_x.$

To prove, observe that all atoms are subsets of X and thus the right-hand side is a subset of X, and that the right-hand side contains all elements of X as the set A_x containing x occurs among the terms for each x$\displaystyle in$X. All there remains to prove is that the representation is unique. If x$\displaystyle in$X, then a representation of X must contain the atom A_x as that is the only atom that contains x. On the other hand, if X and a particular atom are disjoint, it cannot occur in the representation of X.

Let the atoms of S_v be A¹,...,A^k. By the above reasoning, for each set X in S_v there exists a unique index set I$\displaystyle subset${1,2,...,k}, such that X=$\displaystyle cup$_{i$\displaystyle in$I}Aⁱ, and vice versa, for any index set I the set $\displaystyle cup$_{i$\displaystyle in$I}Aⁱ is in S_v. Thus there is a one-to-one correspondence between the sets in S_v and the subsets of the set {1,2,...,k}. The number of such subsets is 2^k, therefore |S_v|=2^k. This completes the proof of the lemma.

Now there remains to prove the statement of the problem. Let the values of the function f be v₁<v₂<...<v_n. Consider the sets S_v₁,S_v₂,...,S_{v_n}. These sets form a chain getting wider and wider:

S_v₁$\displaystyle subset$S_v₂$\displaystyle subset$...$\displaystyle subset$S_{v_n}.

The sets are not empty, and no two of them are identical. It follows from the lemma that |S_v₁|<|S_v₂|<...<|S_{v_n}| are different powers of 2, greater than 1, and thus |S_{v_n}|$\displaystyle ge$2ⁿ. On the other hand, S_{v_n} consists of all the subsets of S, thus |S_{v_n}|=2^|S|. Hence, n$\displaystyle le$|S|.

Remark. It is not hard to construct an example where the range of f has exactly |S| elements. Let S={1,2,...,n}, f(S)=f($\displaystyle emptyset$)=0, and for any subset X different from S and the empty set, let f(X) be the largest number in S, such that exactly one of f(X) and f(X)-1 is an element of X. For example, in the case of n=6, let f({1,2,5})=5.

A. 285. Prove that if a²+ac-c²=b²+bd-d², for the integers a>b>c>d>0, then ab+cd is a composite number.

Solution. Assume that p=ab+cd is a prime. Then ab$\displaystyle equiv$-cd (mod p), and

0=b²(b²+bd-d²)-b²(a²+ac-c²)=b²(b²+bd-d²)-a²b²-ab²c+b²c²$\displaystyle equiv$

$\displaystyle equiv$b²(b²+bd-d²)-c²d²+bc²d+b²c²=(b²+c²)(b²+bd-d²) (mod p).

Therefore, one of the numbers b²+c² and b²+bd-d² is divisible by p.

If p divides b²+c², then it follows from 0<b²+c²<2(ab+cd)=2p that b²+c²=p. In that case, ab+cd=b²+c². Investigation modulo b shows that c(c-d) is divisible by b. b and c are relative primes (or ab+cd could not be a prime), thus c-d is divisible by b. This is contradiction, as 0<c-d<b.

If p divides b²+bd-d², then it follows from 0<b²+bd-d²<2(ab+cd)=p that b²+bd-d²=p. Then ab+cd=b²+bd-d²=a²+ac-c². Investigation modulo a and modulo b shows that (c+d)c is divisible by a, and (c+d)d is divisible by b. As ab and cd are relative primes, it follows that c+d is divisible by both a and b. But that is impossible,as 0<c+d<2a and 0<c+d<2b.

A. 286. Find all continuous functions 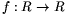$f:R\to R$ such that

$\displaystyle f\left({x+y\over1+xy}\right)={f(x)f(y)\over|1+xy|},$

where 1+xy$\displaystyle ne$0. (based on the idea of Z. Győrfi and G. Ligeti)

Solution. Let

$\displaystyle g(u)=\left|{1+u\over2}\right|\cdot f\left({u-1\over u+1}\right),$

or, what is equivalent,

$\displaystyle f(x)=|1-x|\cdot g\left({1+x\over1-x}\right).$

With a little calculation, it is easy to check that this substitution means g(uv)=g(u)^.g(v). This may happen in three different ways:

a) g(u)$\displaystyle equiv$0; then f(x)$\displaystyle equiv$0.

b) g(u)=|u|^{$\displaystyle alpha$}, where $\displaystyle alpha$ is a real number. Then f(x)=|1+x|^{$\displaystyle alpha$}^.|1-x|^{1-$\displaystyle alpha$}. It follows from continuity that 0$\displaystyle le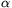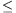$ $alpha$ $le$ 1.

c) g(u)=sgnu^.|u|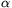. Then f(x)=sgn(1-|x|)^.|1+x|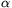^.|1-x|^1-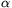. In this case, 0< 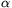$alpha$ <1.

Remark. The fraction 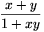${x+y\over1+xy}$ is reminiscent of the addition theorem for hyperbolic tangent:

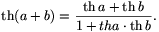
$\th(a+b)={\th a+\th b\over1+tha\cdot\th b}.$

In the solution above, u is substituted for e^2a in the fraction 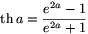$\th a={e^{2a}-1\over e^{2a}+1}$ .

Already signed up?
New to KöMaL?