 |
Solutions for advanced problems "A" in September, 2002 |
In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.
A. 296. Alice has chosen one of the numbers 1,2,...,16. Bob can ask seven yes-no questions to find it out. Alice is allowed to give at most one wrong answer. Help Bob to find out the number in all cases.
Solution. Let us encode the 16 possible numbers by 4-element sequences of zeros and ones. Let the four digits corresponding to the number in question be x1, x2, x3 és x4. Let the seven questions of Bob ask whether the expressions x1, x2, x3, x4, x1+x2+x3, x1+x2+x4, x1+x3+x4 are odd. The answers can also be encoded with zeros and ones as follows: Let V1, V2, V3, V4, V1,2,3, V1,2,4 and V1,3,4 denote the answers. (That is, for example, V1,2,3 is 1 if x1+x2+x3 are odd.)
If V1+V2+V3+V1,2,3 is even , then these answers are correct, and we know x1, x2 and x3. The value of x4 can be obtained from each of the other three answers. Since one answer is allowed to be incorrect, the true value is the one obtained at least twice.
The procedure is the same when either V1+V2+V4+V1,2,4 or V1+V3+V4+V1,3,4 is even.
If V1+V2+V3+V1,2,3, V1+V2+V4+V1,2,4, V1+V3+V4+V1,3,4 are all odd then there is an incorrect answer in each four. The only common element is V1. Thus the other answers are all correct, and each of x1, x2, x3, x4 can be determined from them.
Remark. The problem is related to algebraic code theory, and to the construction of Hamming codes in particular. Let k be a positive integer, h=2k-1 and m=h-k. The "Hamming code (m,h)'' is a set of h-element sequences of zeros and ones, the number of the elements of the set is 2m, and for any sequence of h zeros and ones there exists one unique sequence in the code, such that the two sequences differ in at most one element.
For example, the "Hamming code (4,7)'' consists of the following sequences:
| 0000000 | 0100101 | 1000011 | 1100110 |
| 0001111 | 0101010 | 1001100 | 1101001 |
| 0010110 | 0110011 | 1010101 | 1110000 |
| 0011001 | 0111100 | 1011010 | 1111111 |
The problem is equivalent to finding a construction corresponding to the Hamming code (4,7).
Further reading on code theory: Algebrai Kódelmélet by J. Pelikán (KöMaL 1993/5, pp193-199, in Hungarian).
A. 297. Let a0,a1,... be positive integers such that a0=1, a1>1 and
\(\displaystyle a_{n+1}=\frac{a_1\cdot\ldots\cdot a_n}{a_{[n/2]}}+1\)
for all n=1,2,.... ([x] denotes the integer part of x.) Show that \(\displaystyle \sum_{n=1}^\infty\frac{1}{a_{n+1}a_{[n/2]}}\) is a rational number.
Solution. If N is a positive integer,
\(\displaystyle \sum_{n=1}^N{1\over a_{n+1}a_{[n/2]}} =\sum_{n=1}^N{1\over a_{n+1}\displaystyle{a_1\cdot\dots\cdot a_n\over a_{n+1}-1}} =\sum_{n=1}^N{a_{n+1}-1\over a_1\cdot\dots\cdot a_{n+1}}=\)
\(\displaystyle =\sum_{n=1}^N\left({1\over a_1\cdot\dots\cdot a_n}-{1\over a_1\cdot\dots\cdot a_{n+1}}\right)={1\over a_1}-{1\over a_1a_2\dots a_{N+1}}.\)
Since each of a2,a3,... is greater than 1, \(\displaystyle {1\over a_1a_2\dots a_{N+1}}\le{1\over2^N}\), and thus
\(\displaystyle \sum_{n=1}^\infty{1\over a_{n+1}a_{[n/2]}}={1\over a_1}.\)
A. 298. The angles of a spherical triangle are
\(\displaystyle alpha\), 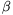 and
and 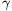 , the lengths
of the opposite side arcs are a, b and c,
respectively. Prove that a.cos
, the lengths
of the opposite side arcs are a, b and c,
respectively. Prove that a.cos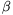 +b.cos\(\displaystyle alpha\)<c.
+b.cos\(\displaystyle alpha\)<c.
Solution. Let O be the centre of the sphere on which the triangle lies, and let A, B, C denote the vertices as usual. We can assume that the radius of the sphere is unity. Consider the sectors OAB, OBC and OCA; their areas are c/2, a/2 and b/2. Now project the three sectors onto the plane OAB. Let C' denote the projection of the point C, and let A' and B' be the antipodal points to A and B, respectively. It follows from the projection that C' falls in the interior of the unit circle centred at O. The projections of the arcs AC and BC are corresponding arcs of an ellipse of major axis AA' and one of major axis BB'. The two ellipse intersect at 4 points altogether: each of the half ellipses joining A to A' intersects each of the half ellipses joining B to B'. There may be no more intersections, since two conic sections cannot intersect at more than 4 points.
The directed areas of the sectors OBC and
OCA (a/2).cos 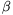 and
(b/2).cos \(\displaystyle \alpha\). The statement of the problem is
therefore equivalent to the sum of the two directed areas being less
than the area of the sector OAB.
and
(b/2).cos \(\displaystyle \alpha\). The statement of the problem is
therefore equivalent to the sum of the two directed areas being less
than the area of the sector OAB.



There are three different cases, depending on which side of the lines AA' and BB' the point C' lies. See the Figure. (For a full solution, the degenerate cases of C' lying on the line AA' or the line BB' also need to be considered but these can be treated together with the above two cases) In the Figure, the green colour indicates the areas that occur with positive signs in the directed areas of the two projected sectors, and the red colour shows the areas with negative signs. In case (b) there is an area that occurs in both projections but with opposite signs. That area is marked blue. egy olyan terület, ami mindkét vetületben szerepel, mégpedig
In each of the three cases, the green areas are disjoint, they are parts of the sector OAB, but they do not cover it completely. Therefore, the sum of the two directed areas is always smaller than the area of the sector
