 |
Exercises and problems in Informatics |
Please read The Conditions of the Problem Solving Competition.
I. 43. Write a program (I43.pas, ...) which computes the maximal value of n such that F(n-1).x+F(n).y=N holds for a given N (2\(\displaystyle \le\)N \(\displaystyle \le\)10 000 000), where F(n) is the nth Fibonacci number, x and y are non-negative integers.
(10 points)
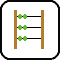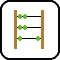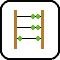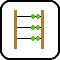
I. 44. Prepare a program (I44.pas, ...) which keeps on rotating an ellipse around the origin (i.e. the centre of the screen) by ALPHA degree in every time step in such a way that meanwhile the ellipse itself is also rotated about its own center by BETA degree in every time step. The ellipse is given by the length of its major and minor axes. In the beginning, the centre of the ellipse is positioned in the middle row of the screen and at \(\displaystyle \frac{3}{4}\) of the maximal number of columns. The program should be able to run for arbitrary many time steps updating the figure in each one.
The example shows the 1st, 4th, 10th and 17th time steps with parameter values ALPHA=60, BETA=70, Major Axis=50, Minor Axis=25.
(10 points)
 |  |  |  | |||
| Step 1 | Step 4 | Step 10 | Step 17 |
I. 45. We generate black and white patterns on a 100x100 sheet in the following way. Relative to the origin (0,0), a point (x,y) is scaled by factors (dx, dy) and translated by the vector (sx,sy) first. Then the square of the distance between the result and the origin is computed and rounded. The corresponding colour of the point (x,y) is black, if this integer is even, otherwise its colour is white.
Prepare a sheet (I45.xls) which, using the values of dx, dy, sx, sy on the second spreadsheet, creates a 100x100 pattern on the first sheet.
The examples show three patterns corresponding to dx=0.25, dy=0.25, sx=0, sy=0, and dx=0.25, dy=0.25, sx=10, sy=20, further dx=0.1, dy=0.1, sx=50, sy=50.
(10 points)
| dx=0,25, dy=0,25, sx=0, sy=0 |
dx=0,25, dy=0,25, sx=10, sy=20 |
dx=0,1, dy=0,1, sx=50, sy=50 |
 |
 |
 |