|
Solutions for advanced problems "A" in September, 2003 |
In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.
A. 323. I is the isogonic point of a triangle ABC (the point in the interior of the triangle for which ∠AIB=∠BIC=∠CIA=120o). Prove that the Euler lines of the triangles ABI, BCI and CAI are concurrent.
Solution 1 (Rácz Béla András, Budapest). We shall prove that the three Euler lines pass through the centroid of triangle ABC. By the symmetry, it is sufficient to prove this for the Euler line of triangle BCI.

Figure 1
Draw a regular triangle onto side BC outside; denote its third vertex by A', its center by O1. The quadrilateral IBA'C is cyclic since BA'C∠+CIB∠=60o+120o=180o. Due to A'B=A'C, line A'I is the angle bisector of ∠CIB and this is the same line as AI (see Figure 1).
Denote the midpoint of BC by F, the centroid of ABC by S and the centroid of BCI by S1. Since FS:FA=FS1:FI=FO1:FA'=1:3, the points S, S1 and O1 lie on the same line. In other words, the Euler line of triangle BCI, which is O1S1, passes through points S, the centroid of ABC.
Solution 2. Let O1, O2 and O3 be the circumcenters of triangles BCI, CAI and ABI, respectively, and let M1, M2, M3 be the orthocenters. The lines O1O2, O2O3, O3O1 are the perpendicular bisectors of CI, AI and BI. Summing up the angles of the three shaded quadrilaterals in Figure 2, it can be obtained that all angles of triangle O1O2O3 are 60o; this triangle is equilateral.

Figure 2
We shall show that the Euler lines of triangles ABI, BCI and CAI pass through the center of triangle O1O2O3. Due to the symmetry, it is sufficient to deal with one of the triangles, say BCI. Since BO1=IO1=CO1, the lines O1O2 and O1O3 are angle bisectors in BO1I∠ and IO1C∠, and thus BO1C∠=2O3O1O2∠=2.60o=120o.

Figure 3
Let point U be the intersection of lines BI and CM1, and let point V be the intersection of CI and BM1. From the quadrilateral M1VIU we obtain CM1B∠=60o. The quadrilateral M1BO1C is cyclic, since CM1B∠+BO1C∠=60o+120o=180o. Then, from BO1=O1C we obtain CM1O1∠=O1M1B∠=30o.
Finally M1O1O2∠= O1M1B∠ and O3O1M1∠=CM1O1∠, thus M1O1O2∠=O3O1M1∠=30o. Hence, the Euler line of triangle BCI, which is O1M1, is the angle bisector of O3O1O2=∠ and passes through the center of triangle O1O2O3.
A. 324. Prove that if a,b,c are positive real numbers then
1a(1+b)+1b(1+c)+1c(1+a)≥31+abc.
Solution 1. The inequality can be transformed to this one:
ab(b+1)(ca-1)2+bc(c+1)(ab-1)2+ca(a+1)(bc-1)2≥0.
Solution 2 (Tamás Birkner, Budapest). Multiply the inequality by (1+abc) and add 3 to both sides.
(1+abca(1+b)+1)+(1+abcb(1+c)+1)+(1+abcc(1+a)+1)≥6
(1+aa(1+b)+b(1+c)1+b)+(1+bb(1+c)+c(1+a)1+c)+(1+cc(1+a)+a(1+b)1+a)≥6
(1+aa(1+b)+a(1+b)1+a)+(1+bb(1+c)+b(1+c)1+b)+(1+cc(1+a)+c(1+a)1+c)≥6.
In the last row, each parentheses have the form x+1x and is at least 2.
Solution 3 (Dobrovolska Galyna, Kiev). Multiplying by (1+abc),
1a(1+b)+abca(1+b)+1b(1+c)+abcb(1+c)+1c(1+a)+abcc(1+a)≥3
1a(1+b)+ab1+a+1b(1+c)+bc1+b+1c(1+a)+ca1+c≥3
1a⋅11+b+b⋅11+1a+1b⋅11+c+c⋅11+1b+1c⋅11+a+a⋅11+1c≥6.\eqno(1)
Since the pairs 1a, b and 11+1a, 11+b are ordered oppositely,
1a⋅11+b+b⋅11+1a≥1a⋅11+1a+b⋅11+b=11+a+b1+b.\eqno(2)
Similarly,
1b⋅11+c+c⋅11+1b≥11+b+c1+c,\eqno(3)
and
1c⋅11+a+a⋅11+1c≥11+c+a1+a.\eqno(4)
Summing up (2), (3) and (4), we obtain (1).
A. 325. We have selected a few 4-element subsets of an n-element set A, such that any two sets of four elements selected have at most two elements in common. Prove that there exists a subset of A that has at least 3√6n elements and does not contain any of the selected 4-tuples as a subset.
Solution. Let N be the set of all selected 4-element subsets. Assume N≠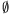 and n
and n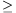 4 (If n
4 (If n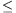 2 and N=
2 and N=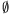 , then the statement fails since
, then the statement fails since 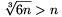 .)
.)
Call a subset of A ``good'' if no element of N is its subset. Trivially, the subsets of 3 or less elements, including the empty set, are all good. A good subset is called maximal if it has no good superset. There exists at least one maximal good subset, because starting from a good subset, new elements can be added one by one while it is possible.
We shall prove that each maximal good subset has more than 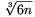 elements. Then any maximal good subset proves the statement.
elements. Then any maximal good subset proves the statement.
Let M be an arbitrary maximal good subset of A, and |M|=k. Clearly k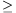 3, because all 3-element subsets are good. If
3, because all 3-element subsets are good. If 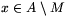 is an arbitrary element, then the set M
is an arbitrary element, then the set M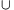 {x} is not good. This means that x and some 3 elements of M form an element of N. Denote one of such triplets by h(x).
{x} is not good. This means that x and some 3 elements of M form an element of N. Denote one of such triplets by h(x).
If 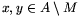 are two different elements, then the sets H1=h(x)
are two different elements, then the sets H1=h(x)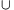 {x} and H2=h(y)
{x} and H2=h(y) {y} are elements of N. These two elements are different, because, for example, x
{y} are elements of N. These two elements are different, because, for example, x H1 but
H1 but  . Then H1 and H2 have at most 2 common elements. This implies h(x)
. Then H1 and H2 have at most 2 common elements. This implies h(x) h(y).
h(y).
Consider now all triplets h(x). We have n-k such triplets, they are pairwise different. The set M has 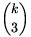 3-element subsets, thus
3-element subsets, thus 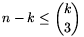 . From this inequality we have
. From this inequality we have
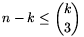
6n k3-3k2+8k=k3-k(3k-8)<k3
k3-3k2+8k=k3-k(3k-8)<k3