Exercises and problems in Informatics December 2003

Please read The Conditions of the Problem Solving Competition.

I. 64. The Farey sequence F_N for any positive integer N is the sequence of irreducible rational numbers between 0 and 1 for which the denominator is at most N and they are arranged in increasing order. For example, $\displaystyle F_6=\left\{\frac{0}{1},\, \frac{1}{6},\,\frac{1}{5},\,\frac{1}{4},\,\frac{1}{3},\, \frac{2}{5},\,\frac{1}{2},\,\frac{3}{5},\,\frac{2}{3},\, \frac{3}{4},\,\frac{4}{5},\,\frac{5}{6},\,\frac{1}{1} \right\}.$

For any given N (1$\displaystyle \le$N $\displaystyle \le$100), your program (i64.pas, ...) should display the Farey sequence F_N.

(10 points)

I. 65. Given N+1 points (x_i,y_i) in the plane, a Bézier curve nicely approximating them is given by its coordinate-functions x and y in the following parametric form (with 0$\displaystyle \le$u $\displaystyle \le$1 being a real parameter):

$\displaystyle x(u)=\sum_{i=0}^nx_i{n\choose i}u^i(1-u)^{n-i},\quad y(u)=\sum_{i=0}^ny_i{n\choose i}u^i(1-u)^{n-i}.$

Write your program (i65.pas, ...) which reads the coordinates of the N+1 points then draws them together with the corresponding Bézier curve.

Example.:

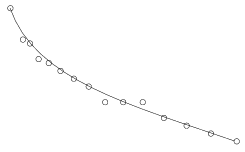
N=14 The points: (0,0),(16,40),(25,45), (36,65),(49,70),(64,80), (81,90),(100,100),(121,120), (144,120),(169,120),(196,140), (225,150),(256,160),(289,170)

(10 points)

I. 66. Euler's number triangle is similar to Pascal's triangle, but instead of the binomial coefficients, it contains the Eulerian numbers E(n,k). For 0$\displaystyle \le$n $\displaystyle \le$15 and 0$\displaystyle \le$k $\displaystyle \le$n, E(n,k) is defined as the number of permutations of {1,2,...,n} having exactly k permutation ascents (i.e. having k pairs of adjacent positions in the permutation that are out of order).

Prepare your sheet (i66.xls) that - on entering the value of m (0$\displaystyle \le$m$\displaystyle \le$15) into cell <<\texttt>>A1 - displays the Eulerian numbers E(n,k) (n=0,1,...,m) in the first n+1 rows of the sheet. Numbers should only appear in valid cells.

Example for m=10:

Send your solutions to the following e-mail address:

infotech@komal.elte.hu.

Deadline: 13 January 2004