A geometriai elrendezések diszkrét bája
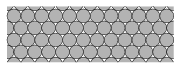
A magyar matematika a Bolyaiaktól kezdve, Riesz Frigyesen és Fejér Lipóton keresztül kortársainkig számos ragyogó nagyságot adott a világnak. Zseniális egyéniségeket, akik meghatározó eredményeket értek el a matematika egyik-másik ágában. De alig volt közöttük az olyan, nagy formátumú, iskolateremtő tudós, aki tanítványok tucatjaiban keltette fel az érdeklődést kutatási témája iránt, és indította el őket a matematikusi pályán. A ritka kivételek egyike a néhány hete, 90 éves korában elhunyt Fejes Tóth László. Erdős Pálhoz, Neumann Jánoshoz és Turán Pálhoz hasonlóan ő is Fejér Lipótnál doktorált a Pázmány Péter Tudományegyetemen. Két évi katonáskodás után, 1941-ben a Kolozsvári Egyetemre került. A később munkaszolgálatosként elpusztult Lázár Dezsőtől ott hallott először azokról a geometriai problémákról, melyek egész pályáját meghatározták. A legegyszerűbb kérdés úgy hangzott, hogy miként lehet elhelyezni egy ,,nagy'' asztalon a lehető legtöbb egyforintost? Az állítást, miszerint a legjobb elrendezésben az asztal szélére tett érméktől eltekintve az összes egyforintost hat másik érinti, először Axel Thue, norvég számelmélész bizonyította 1892-ben. A bizonyítás korántsem magától értetődő. A térben azt kérdezhetjük, hogy legfeljebb hány egységnyi átmérőjű gömb fér bele egy hatalmas tartályba? Ugyan a probléma egyes vonatkozásait Minkowski és Hilbert is érintette, fél évszázadon keresztül főképp kristallográfusok és fizikusok foglalkoztak vele. Érdeklődésük abból a meggyőződésből fakadt, hogy nagy nyomás alá helyezett homogén anyag atomjai vagy molekulái automatikusan a legsűrűbb kristályszerkezetbe rendeződnek. A lehetséges szabályos kristályszerkezetek teljes leírása a 19. század végére lényegében befejeződött. Így elvileg - rendkívül hosszadalmas számítások útján - tetszőleges alakú molekulák (vagy más objektumok) esetén nagy pontossággal meghatározható a legsűrűbb szabályos ,,rácsszerű'' elrendezés. De mi a helyzet, ha a legsűrűbb elrendezés nem szabályos? Ez a kérdés akkoriban a kutatók zömében fel sem merült. Fejes Tóth László megsejtette, hogy mély matematikai problémáról van szó, amely szorosan összefügg a klasszikus analízis, approximációelmélet és algebra fontos területeivel. A nem rácsszerű szerkezetek és kvázikristályok vizsgálata mára önálló tudományággá vált. Ebben a folyamatban lehetetlen túlbecsülni Fejes Tóth László személyes szerepét. Még a háború befejezése előtt tucatnyi alapvető dolgozatot szentelt ilyen típusú kérdéseknek. Később a budapesti Árpád Gimnázium, majd 1949-től a Veszprémi Vegyipari Egyetem tanáraként szinte egymaga kidolgozta a ,,geometriai elrendezések'' elméletét ,,a síkon, a gömbfelszínen és a térben''. Német nyelvű monográfiája, amely 1953-ban hasonló címmel jelent meg Berlinben a Springer kiadó legrangosabb matematikai könyvsorozatában, a témakör máig meghatározó klasszikusa, bibliája. Nem sokkal később C. A. Rogers, neves angol matematikus így fogalmazott: ,,Eddig az elhelyezések és fedések elmélete túlságosan fejletlen volt ahhoz, hogy egy teljes könyvet szentelhessünk neki. Fejes Tóth munkájának publikálása után viszont úgy tűnhet, hogy ebben a témakörben további könyvre nincs szükség.'' Ahhoz, hogy a Fejes Tóth László könyvében vizsgált alapproblémát pontosan megfogalmazzuk, be kell vezetnünk néhány definíciót és jelölést. Legyen C egy T(C)-területű zárt síkidom, \(\displaystyle \mathcal{C}=\{C_1,C_2,C_3,\ldots\}\) pedig C-vel egybevágó halmazok egy rendszere a síkon. A \(\displaystyle \mathcal{C}\) rendszert elhelyezésnek (vagy pakolásnak) nevezzük, ha semelyik két elemének nincs közös belső pontja. Jelöljük még az origó körüli r sugarú kört Br-rel. 1. ábra. A legsűrűbb rácsszerű körelhelyezés Ha egy \(\displaystyle \mathcal{C}\) elhelyezésnek k eleme esik Br-be, akkor a \(\displaystyle \frac{kT(C)}{T(B_r)}\) hányadost \(\displaystyle \mathcal{C}\) sűrűségének nevezzük az r-sugarú körben. Tegyük fel, hogy ezek a sűrűségek egy \(\displaystyle \delta(\mathcal{C})\) határértékhez tartanak, amennyiben r\(\displaystyle \to\) A C halmaz eltolt példányaiból álló elrendezések között speciális szerepet töltenek be az úgynevezett rácsszerű elrendezések. Ezek azon halmazokból állnak, melyek véges sok lépésben megkaphatóak C-ből úgy, hogy minden egyes lépésben az előzőleg konstruált halmazt egy rögzített u vektorral vagy v vektorral előre vagy hátra toljuk. Az u és v vektorokat a rácsszerű elrendezés generátorainak hívjuk. A C halmaz rácspakolási együtthatója a Fejes Tóth Lászlónak sikerült belátnia, hogy minden középpontosan szimmetrikus konvex C síkidomra Ebből az is levezethető, hogy 2. ábra. A sejthető legsűrűbb félkörelhelyezés A fenti fogalmak természetesen kiterjeszthetőek 3-dimenziós testekre is. Érdekes nyitott kérdés, hogy vajon minden 3-dimenziós konvex C testre teljesül-e Az 1953-ban publikált mű, melyet oroszra és japánra is lefordítottak, egycsapásra világhírnevet szerzett Fejes Tóth Lászlónak. A világhírnév pedig meghozta a hazai elismerést, a Kossuth-díjat és 1962-ben az akadémiai tagságot. Fejes Tóth rendkívül szerény, puritán, tisztességes ember volt, aki szinte naiv módon hitt a ,,tiszta ész'' erejében és kereste az igazságot. Biztos, hogy ezek a tulajdonságok különösen értékesek a tudományos kutatásban. Sosem hajlott meg semmilyen hatalom vagy tekintélyelv előtt. Csak hosszas rábeszélés után vállalta, hogy 1970-től 1983-ig ő vezesse az Akadémia Matematikai Kutató Intézetét. Személye garancia volt arra, hogy az akkoriban erősen megosztott matematikai közélet viharai ne törjenek be az intézet falai közé, a munka zavartalanul folyjék. Ottlik szavaival: ő ,,szavatolt a Lady biztonságáért''. A matematikusok egyik Mekkája az Oberwolfachi Matematikai Kutató Intézet. A Fekete Erdő egy elvarázsolt szögletében található intézményt a második világháború végén a német kormány alapította eredetileg hadi célokra, de ezt a funkcióját sosem látta el. A hatvanas években felépített gyönyörű nemzetközi konferenciacentrumban, melyet eredetileg részben háborús jóvátételi pénzekből finanszíroztak, hétről-hétre más matematikai téma legjelesebb művelői találkoznak. Amikor 1962-ben az Intézet először rendezett diszkrét geometriai konferenciát, szinte magától értetődött, hogy ennek szervezésével és a tudományos program összeállításával Fejes Tóth Lászlót bízzák meg. Amint az Akadémiai Aranyérem odaítélésének hivatalos indoklásában áll: ,,a diszkrét geometria világviszonylatban is az ő tevékenysége nyomán vált önálló tudományággá''. A szakmai elismerés büszkeséggel töltötte el, de a számos díj és kitüntetés, melyben része volt, ellenkezett puritán természetével, a velük járó külsőségek pedig kifejezetten feszélyezték. Hallani sem akart arról, hogy Akadémiai Aranyéremre javasolják. Az 1962-ben rendezett oberwolfachi konferenciának még csak három magyar résztvevője volt. Húsz esztendővel később Fejes Tóth László már népes magyar csoport élén érkezett Oberwolfachba. Időközben nemzetközi hírű iskolát sikerült létrehoznia Budapesten. Tehetséges tanítványok és kollégák generációit vezette be a diszkrét geometria rejtelmeibe. Kivételes - talán csak Erdős Páléhoz hasonlítható - problémafelvető készségével mindenkit lenyűgözött. A tanulmányi versenyeken edződött ifjú magyar matematikus titánok hagyományosan jó feladatmegoldók, Fejes Tóth László pedig ontotta az egyszerűen megfogalmazható, gyönyörű kérdéseket. Lehet, hogy középiskolai tanári múltja is közrejátszott abban, hogy mindig ügyelt az egyszerű fogalmazásra és az esztétikai szempontokra. Utálta a bonyolult jelöléseket és a ,,magas matematika'' nagyképű fogalmainak felesleges használatát. A feladatok között szép számmal akadt olyan, amely néhány szellemes ötlet segítségével - vagy éppen kitartó aprómunkával - viszonylag könnyen megoldható. Aki a sikeren felbuzdulva megpróbált mélyebbre ásni, és hozzálátott Fejes Tóth László soronkövetkező feladatának megoldásához, az gyakran leküzdhetetlennek látszó akadályokba ütközött. Ha volt benne kitartás és tehetség, akkor olyan izgalmas kutatási területre bukkant, melynek feltárása sok évre elegendő gondolkodnivalóval szolgált [6]. Fejes Tóth László rendkívül nagyra értékelt minden mérhető teljesítményt, ami mögött kemény munka és tehetség áll. Imádta a sportot. Kiválóan pingpongozott, teniszezett, szertornázott. Egy megkopott fénykép mutatja, amint közel ötven évesen óriáskört csinál a nyújtón. Mintaszerűen lefeszített lábfeje az ég felé mutat. Szinte repül. Sok évvel később, túl a hatvanon még magasabbra tört. Stuttgarti vendégprofesszorsága idején a sárkányrepülést is megtanulta. Matuzsálemi kort ért meg. Megkerülhetetlen, impozáns, teljes életművet hagyott maga után. A sors különleges adományának tekintem, hogy tanítványa, munkatársa, tisztelője és - a nagy korkülönbség dacára talán kicsit - a barátja is lehettem. Szakmai és emberi szempontból ő volt és marad számomra az etalon. Pach János Irodalom [1] L. Fejes Tóth: Lagerungen in der Ebene auf der Kugel und im Raum, Zweite Aufl., Springer-Verlag (Berlin, 1972). [2] L. Fejes Tóth: Regular Figures, Pergamon Press (Oxford, 1964). [3] Fejes Tóth László: Lencsék legsűrűbb elhelyezése a síkban, Matematikai Lapok, 22 (1971), 209-213. [4] L. Fejes Tóth: Densest packing of translates of the union of two circles, Discrete and Computational Geometry, 1 (1986), 307-314. [5] T. C. Hales: Cannonballs and honeycombs, Notices Amer. Math. Soc., 47 (2000), 440-449. [6] P. Brass, W. Moser and J. Pach: Research Problems in Discrete Geometry, Springer-Verlag (New York, 2005). [7] http://www.math.pitt.edu/~thales/kepler04/ (Fejes Tóth László emlékezetére)
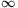 . Nem nehéz belátni, hogy
. Nem nehéz belátni, hogy 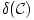 nem függ az origó megválasztásától. Definiáljuk a C síkidom
nem függ az origó megválasztásától. Definiáljuk a C síkidom  (C) pakolási együtthatóját, mint a
(C) pakolási együtthatóját, mint a 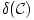 határértékek összes
határértékek összes 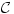 elhelyezésre vett maximumát. Tehát a
elhelyezésre vett maximumát. Tehát a 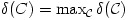 szám durván azt fejezi ki, hogy a sík területének legfeljebb mekkora hányada tölthető ki átfedés nélkül C egybevágó példányaival. Hasonlóképpen definiálhatjuk C eltolásokkal való pakolási együtthatóját, a
szám durván azt fejezi ki, hogy a sík területének legfeljebb mekkora hányada tölthető ki átfedés nélkül C egybevágó példányaival. Hasonlóképpen definiálhatjuk C eltolásokkal való pakolási együtthatóját, a 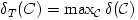 számot, kivéve, hogy most a maximumot csak azokra a
számot, kivéve, hogy most a maximumot csak azokra a 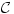 elhelyezésekre kell vennünk, melyek C eltolt példányaiból állnak.
elhelyezésekre kell vennünk, melyek C eltolt példányaiból állnak.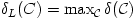 szám, ahol a maximumot ezúttal C rácsszerű elhelyezéseire vesszük. Világos, hogy
szám, ahol a maximumot ezúttal C rácsszerű elhelyezéseire vesszük. Világos, hogy L(C)
L(C)
 T(C)
T(C)
 (C).
(C). L(C)=
L(C)=  T(C)=
T(C)=  (C).
(C). L(C)=
L(C)= T(C) minden síkbeli konvex halmazra. Viszonylag egyszerű szerkezetű C halmazok esetén a
T(C) minden síkbeli konvex halmazra. Viszonylag egyszerű szerkezetű C halmazok esetén a  L(C) szám általában elég pontosan meghatározható. A középpontos szimmetria feltételezése nélkül viszont
L(C) szám általában elég pontosan meghatározható. A középpontos szimmetria feltételezése nélkül viszont  (C) meghatározása sok esetben nehéznek látszik. Máig nem ismeretes például, hogy mennyi a félkör pakolási együtthatója [3]. Egy másik szép - és talán nem reménytelenül nehéz - megválaszolatlan kérdés, amely Fejes Tóth Lászlótól származik, a következő: Igaz-e, hogy minden olyan összefüggő C síkidomra, amely előáll két konvex halmaz egyesítéseként, érvényes a
(C) meghatározása sok esetben nehéznek látszik. Máig nem ismeretes például, hogy mennyi a félkör pakolási együtthatója [3]. Egy másik szép - és talán nem reménytelenül nehéz - megválaszolatlan kérdés, amely Fejes Tóth Lászlótól származik, a következő: Igaz-e, hogy minden olyan összefüggő C síkidomra, amely előáll két konvex halmaz egyesítéseként, érvényes a  L(C)=
L(C)= T(C) egyenlőség? [4]
T(C) egyenlőség? [4]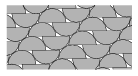
 L(C)=
L(C)= T(C). Az utóbbi tíz év talán egyik legnagyobb port felvert matematikai fejleménye az a máig is csak részben publikált cikksorozat volt, melyben Tom Hales megkísérelte az úgynevezett Kepler sejtés bizonyítását [5], vagyis annak igazolását, hogy a 3-dimenziós B3 egységgömbre
T(C). Az utóbbi tíz év talán egyik legnagyobb port felvert matematikai fejleménye az a máig is csak részben publikált cikksorozat volt, melyben Tom Hales megkísérelte az úgynevezett Kepler sejtés bizonyítását [5], vagyis annak igazolását, hogy a 3-dimenziós B3 egységgömbre  (B3)=
(B3)=  L(B3). A sajtóközlemények nagy teret szenteltek annak a körülménynek, hogy Hales gigantikus munkája lényegében azt a programot váltja valóra kiterjedt számítógépes segédlettel, amelyet Fejes Tóth László könyvében negyven évvel korábban felvázolt. Természeténél fogva Hales érvelésének ellenőrzése maga is rendkívül bonyolult számítógépes módszereket igényel, így annak helyességéről máig megoszlanak a vélemények.
L(B3). A sajtóközlemények nagy teret szenteltek annak a körülménynek, hogy Hales gigantikus munkája lényegében azt a programot váltja valóra kiterjedt számítógépes segédlettel, amelyet Fejes Tóth László könyvében negyven évvel korábban felvázolt. Természeténél fogva Hales érvelésének ellenőrzése maga is rendkívül bonyolult számítógépes módszereket igényel, így annak helyességéről máig megoszlanak a vélemények.

Informatika rovattal
Kiadja a MATFUND Alapítvány
| Már regisztráltál? | |
| Új vendég vagy? |
