Beszámoló a 2007. évi Eötvös-versenyről

2007. október 26-án délután 3-tól este 8-ig zajlott az 1949-es felújítása óta immár ötvenkilencedik Országos Eötvös Loránd Fizikaverseny, népszerű nevén Eötvös-verseny. Az ország 15 városában várták a verseny helyi szervezői azokat a diákokat, akik vagy még középiskolások voltak ebben a tanévben, vagy 2007-ben fejezték be középiskolai tanulmányaikat. (Nem csak magyar állampolgárságú, hanem külföldi diákok is indulhatnak az Eötvös-versenyen, akik magyar nyelven tanulják/tanulták a fizikát Magyarországon, vagy valamelyik környező országban.) A feladatokat a Versenybizottság állítja össze, ennek elnöke Radnai Gyula, tagjai Gnädig Péter, Honyek Gyula és Károlyházy Frigyes. Megoldási idő 300 perc; a megoldáshoz bármilyen írott vagy nyomtatott könyv, füzet felhasználható, amit a diák magával hoz a versenyre. Saját zsebszámológépét is használhatja, de természetesen a verseny ideje alatt nem használhat mobiltelefont. A beérkezett dolgozatokat a Versenybizottság bírálja el, dönt a díjakról, dicséretekről.

Ebben az évben 109 versenyző adott be megoldást a feladatokra. Tovább csökkent a középiskolás versenyzők száma, míg az érettségizetteké valamennyire stabilizálódott. Legtöbben idén is a Fővárosi Fazekas Mihály Gyakorló Gimnáziumból jöttek és adták be dolgozataikat.

Ismertetjük a feladatokat, s azok helyes megoldását.

1. Két téglalap alakú üveglemezt egyik élük mentén egymáshoz támasztunk úgy, hogy 2\(\displaystyle \varphi\) szöget zárjanak be egymással. Az így rögzített lemezeket lassan vízbe engedjük az ábrán látható módon. A víz, amely tökéletesen nedvesíti az üveget, a felületi feszültség hatására a két lemez között bizonyos H magasságig felemelkedik.

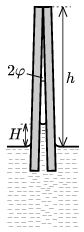
1. ábra

Mekkora ez a H magasság, ha a lemezek vízszintesen tartott érintkezési vonala

a) h=30 mm,

b) h=15 mm, távolságra van a szabad vízfelszíntől? Ábrázoljuk vázlatosan, hogyan változik H a fokozatosan csökkenő h függvényében!

Feltehetjük, hogy a lemezek egymással érintkező éle sokkal hosszabb, mint h, továbbá a lemezek szimmetriasíkja mindvégig függőleges.

Adatok: \(\displaystyle \sigma_{\text{víz}}=0{,}072~\rm N/m,\) \(\displaystyle \varrho_{\text{víz}}=1000~\rm kg/m^3,\) 2\(\displaystyle \varphi\)= 6^o.

(Varga István feladata)

Megoldás. Mivel a két üveglemez elég kis szöget zár be egymással, a köztük felemelkedő víz felületét jó közelítéssel vehetjük félhenger alakúnak. Így felírhatjuk (a félhenger sugarát r-rel jelölve):

\(\displaystyle \varphi\approx\mathop{\rm tg}\varphi=\frac{r}{h-H}. \)

Mechanikai egyensúly esetén a víz felületi feszültségéből adódó görbületi nyomásnak és a felemelkedett vízoszlop H magasságának megfelelő hidrosztatikai nyomásnak meg kell egyeznie, vagyis

\(\displaystyle \frac{\sigma}{r}=H\varrho g. \)

(Azért nem \(\displaystyle \frac{2\sigma}{r}\) a görbületi nyomás, mert a felszín nem gömb, hanem henger alakú.)

Amíg \(\displaystyle \frac{\sigma}{r\)H\varrho g">, addig a folyadékszint még emelkedik az üveglapok között. Ha pedig már túlfutott és \(\displaystyle H\varrho \)\frac{\sigma}{r}"> lett, akkor a vízszint csökkenni kezd. A kialakuló állapot stabil egyensúlyi állapot kell, hogy legyen.

Vizsgáljuk meg, milyen H értékre teljesül a

\(\displaystyle \frac{\sigma}{(h-H)\varphi}=H\varrho g \)

egyensúlyi feltétel! Átalakítva és az ismert adatokat behelyettesítve

\(\displaystyle H(h-H)=\frac{\sigma}{\varrho g\varphi}=1{,}4\cdot10^{-4}~{\rm m}^2=140~{\rm mm}^2. \)

A magasságokat mm-ben mérve az alábbi másodfokú egyenletet kell megoldanunk:

H²-hH+140=0.

Ennek h=30 mm esetén két megoldása lesz: H₁=5,8 mm és H₂= 24,2 mm. E kettő közül azonban csak az egyik, a kisebb érték a stabil, a másik instabil egyensúlyi állapotot határoz meg! A stabilitási viszonyokat is megvizsgálhatjuk, ha H függvényében ábrázoljuk a \(\displaystyle \varrho\)gH és a \(\displaystyle \frac{\sigma}{(h-H)\varphi}\) kifejezéseket (2. ábra). Attól függően, hogy melyik kifejezés a nagyobb, a víz felszíne a bejelölt nyilacskáknak megfelelően fel- vagy lefelé mozog. Látható, hogy H₁ a stabil, H₂ pedig az instabil megoldás.

2. ábra

A fenti ábra addig helyes, amíg

\(\displaystyle \)\sqrt{4\cdot140}=23{,}7~\rm mm, ">

ekkor pozitív ugyanis a fenti másodfokú egyenlet diszkriminánsa.

De mi történik akkor, amikor az üveglapok lassú leengedése közben elérjük a h=23,7 mm értéket, és még tovább süllyesztjük az üveglapokat? h=23,7 mm esetén \(\displaystyle H=\frac{h}{2}\) magasan áll a vízszint, majd a következő pillanatban (amikor a 2. ábrán látható hiperbolának és az egyenesnek már nem lesz metszéspontja, tehát a görbületi nyomás minden helyzetben nagyobb lesz, mint a hidrosztatikai nyomás) a víz emelkedni kezd és egészen a két üveglap érintkezéséig felszalad! Ettől kezdve H=h lesz végig.

Hogyan változik H a fokozatosan csökkenő h függvényében? A választ a 3. ábra mutatja, a kérdéses helyzetekben pedig a numerikus értékek:

a) h=30 mm esetén H=5,8 mm;

b) h=15 mm esetén H=15 mm.

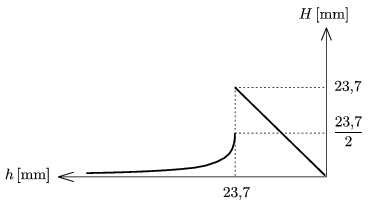
3. ábra

Megjegyzések: A feladatra adott hibás megoldások közül három tipikusat érdemes külön is megemlíteni.

1. Többen a körkeresztmetszetű, függőleges hajszálcsőben felemelkedő vízre érvényes képletet próbálták meg itt alkalmazni. (Ekkor jelenik meg a \(\displaystyle \frac{2\sigma}{r}\) görbületi nyomás!) Nem kaphattak helyes eredményt.

2. Sokan a felemelkedett vízmennyiség súlyát tették egyenlővé a felületi feszültségből származó, felfelé húzó erővel. Ez azért hibás, mert a ferde, nem függőleges üveglemezek által kifejtett nyomóerőnek is van függőleges összetevője, amit az erőegyensúlynál figyelembe kellene venni. A probléma hasonló ahhoz, ami a jól ismert hidrosztatikai paradoxonnál jelentkezik.

3. Néhányan energetikailag próbálták megoldani a feladatot úgy, hogy a felemelkedett víz helyzeti energiáját tették egyenlővé a felületi feszültség \(\displaystyle \sigma\)^.\(\displaystyle \Delta\)A munkájával. Ez ugyanúgy hibás, mintha egy rugóra függesztett test egyensúlyi helyzetének meghatározásához a nehézségi erő és a rugóerő munkájának egyenlőségét írnánk fel. Jól tudjuk, hogy ez az egyenlőség csak a rugón rezgő test mozgásának szélső helyzeteire teljesül, ahol éppenhogy nincs a test egyensúlyban. Egyensúlyi állapotban a mozgási energia nem hanyagolható el, sőt, éppen akkor maximális!

2. Egy terebélyes vasmaggal ellátott, nagy önindukciójú, de mégis elhanyagolható ohmikus ellenállású tekercs végeit U feszültségre méretezett izzón keresztül kötjük össze. Ha az A és B pontok közé U/2 effektív értékű váltakozó feszültséget kapcsolunk, az izzó nagyon halványan világít.

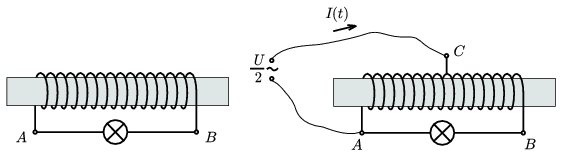
4. ábra

Mivel a tekercs közepéről is van egy C kivezetés, megpróbáljuk a feszültségforrás pólusait az A és C pontokhoz kötni. Megváltozik-e az izzón átfolyó áram erőssége, és ha igen, hogyan? Az ábrán bejelöltük a főágban folyó I(t) pillanatnyi áram irányát. Hogyan folyik az áram ugyanekkor a tekercsben?

(Károlyházy Frigyes)

Megoldás. Három dolgot kell egymás után észrevennünk, hogy viszonylag gyorsan eljussunk a helyes válaszhoz.

1. Mivel a tekercs ohmikus ellenállása elhanyagolható, ezért \(\displaystyle U_{AC}\approx\frac{U}{2}\) kell legyen, hogy ne folyjék a generátoron végtelen nagy áram.

2. Mivel a fluxusváltozás mértéke a tekercs különböző részein ugyanakkora, ezért mindkét féltekercsen ugyanakkora az indukált feszültség, tehát U_AC=U_CB.

3. Mivel a lámpa párhuzamosan van kapcsolva a generátor plusz a tekercs jobb oldali felével, ezért

\(\displaystyle U_{\text{lámpa}}=U_{\text{gen.}}+U_{CB}=\frac{U}{2} +\frac{U}{2},\quad\text{tehát}\quad U_{\text{lámpa}}=U. \)

Így a lámpa az ,,üzemi'' feszültséget kapja, ezért jól ég!

Az áramirányok meghatározásához - Werner Miklós ötlete alapján - rajzoljuk át a megadott kapcsolást a következő módon: képzeljük el, hogy a tekercs bal oldali részét alkotó huzalt hosszában kettévágjuk, s így ezen az oldalon két, egymás mellett futó tekercshez jutunk (5. ábra).

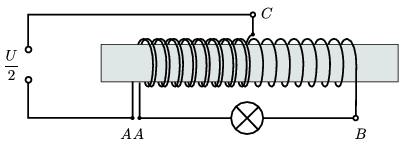
5. ábra

Kaptunk egy AC tekercset, amire a generátor feszültségét kapcsoljuk, és egy AB tekercset, amire a lámpát kötöttük. Ez bizony egy transzformátor! A primer menetszám \(\displaystyle \frac{N}{2}\), a primer áram (a feladatban alkalmazott jelölés szerint) I. A szekunder menetszám N, tehát a szekunder áram \(\displaystyle \frac{I}{2}\) lesz.

C-től B felé \(\displaystyle \frac{I}{2}\), C-től A felé ugyancsak \(\displaystyle \frac{I}{2}\) \(\displaystyle \left(I-\frac{I}{2}=\frac{I}{2}\right)\) áram folyik (6. ábra).

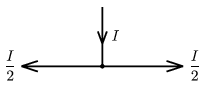
6. ábra

Megjegyzések. Bemutatunk további három megoldást, amellyel a versenyzők eljutottak a helyes válaszhoz. Mindegyikük ,,ráérzett'' a feladatban rejlő transzformátorra (ténylegesen autotranszformátornak nevezik a feladatban megadott kapcsolást), és helyesen alkalmazták az általuk ismert összefüggéseket. Nem részletezzük, csak vázoljuk a megoldásnál követett gondolatmeneteket.

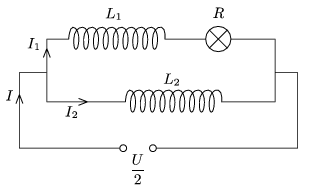
7. ábra

1. Konczer József a 7. ábrán látható módon rajzolta át a kapcsolást. Figyelembe véve a tekercsrészek közötti szoros csatolást, a kölcsönös indukciós együttható: \(\displaystyle M=\sqrt{L_{1}L_{2}}\). Az indukált feszültségek:

\(\displaystyle U_{1}=-L_{1}\frac{\Delta I_{1}}{\Delta t}+M\frac{\Delta I_{2}}{\Delta t}, \)

illetve

\(\displaystyle U_{2}=-L_{2}\frac{\Delta I_{2}}{\Delta t}+M\frac{\Delta I_{1}}{\Delta t}. \)

Mivel most L₁=L₂=L=M, ezért

U₁+U₂=0.

A generátor feszültsége:

\(\displaystyle \frac{U}{2}=-U_{2}=I_{1}R-U_{1}, \)

ebből pedig I₁R=U következik.

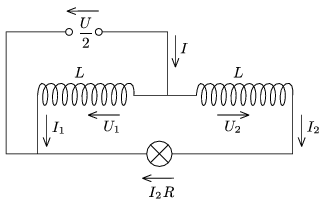
8. ábra

2. Kónya Gábor a 8. ábrán látható módon rajzolta át a kapcsolást. A szinuszos váltakozó áram tárgyalására kidolgozott komplex formalizmus ismeretében ő az alábbi egyenleteket tudta felírni:

U₁=j\(\displaystyle \omega\)L(I₁-I₂),

illetve

U₂=j\(\displaystyle \omega\)L(I₂-I₁).

ezekből következik, hogy U₂=-U₁. Mivel

\(\displaystyle U_{1}=U_{2}+I_{2}R\qquad\text{és}\qquad U_{1}=\frac{U}{2}, \)

ezért

\(\displaystyle \frac{U}{2}=-\frac{U}{2}+I_{2}R,\qquad\text{vagyis}\qquad U=I_{2}R \)

kell legyen. (j-vel az ún. komplex egységgyököt, \(\displaystyle \sqrt{-1}\)-et jelöltük.)

3. Szolnoki Lénárd úgy rajzolta át a kapcsolást (9. ábra), hogy még jobban emlékeztessen egy veszteségmentes, zárt vasmagú transzformátorra. Mivel a transzformátor szekunder oldalán ellentétes ,,irányú'' a feszültség, mint a primer oldalon, ezért a felső hurokra felírva a második Kirchhoff-törvényt, kapjuk:

\(\displaystyle \frac{U}{2}+\frac{U}{2}-U^*=0,\qquad{\text{tehát}}\qquad U^*=U. \)

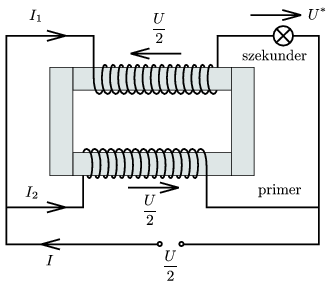
9. ábra

Mindhárom megoldó már a saját rajzán helyesen jelölte be az áramok irányát.

3. Egy tanár az alábbi problémát tűzi ki tehetséges diákjai számára: Vizsgáljátok meg elméletileg, hogy helyettesíthető-e egy vékony gyűjtőlencséből és egy vele párhuzamos síktükörből álló optikai rendszer egyetlen homorú tükörrel!

Anna megvizsgál egy olyan esetet, amikor a gyűjtőlencse f fókusztávolsága 30 cm, és a lencse \(\displaystyle \ell\)= 20 cm-re helyezkedik el a tükör előtt. Ügyesen megválasztott tárgytávolságok felhasználásával meg tudja határozni a keresett homorú tükör f^* fókusztávolságát és e tükörnek a lencse helyétől mért x távolságát.

Balázs általánosan akarja megoldani a feladatot, és addig nem nyugszik, míg olyan összefüggéseket nem talál, melyek megadják f^*-ot és x-et f és \(\displaystyle \ell\) függvényében.

Cecília végül észreveszi, hogy nem minden f és \(\displaystyle \ell\) értékpár esetén helyettesíthető homorú tükörrel a fenti optikai rendszer, ezért átgondolja, hogy milyen feltétel teljesülése esetén érvényes Balázs megoldása.

Kövessük nyomon Anna, Balázs és Cecília munkáját! Hogyan oldják meg a maguk elé tűzött feladatokat?

(Honyek Gyula)

Megoldás. Első ránézésre is látszik, hogy ha helyettesíthető ez a lencse + síktükör együttes egyetlen homorú tükörrel, akkor annak geometriai középpontja ott lesz, ahol most a lencse egyik, F₁ fókuszpontja van. Ha ugyanis ebbe a fókuszba helyezünk egy világító, pontszerű fényforrást, akkor az innen kiinduló fénysugarak a lencsén való áthaladás után az optikai tengellyel párhuzamosan haladnak, merőlegesen érik el a tükör síkját, utána önmagukba verődnek vissza. A síktükörről visszavert sugarak újra elérik a lencsét s azon megtörve a lencse előbbi, F₁ fókuszpontja felé tartanak. Gömbtükör esetén pedig a gömb \(\displaystyle O_\text{tükör}\) középpontjából kiinduló fénysugarak verődnek úgy vissza, hogy ugyanezen pont felé tartanak.

Könnyen megszerkeszthetjük annak a tárgynak a képét, amelyet a lencse fókuszpontjába állítottunk (10. ábra).

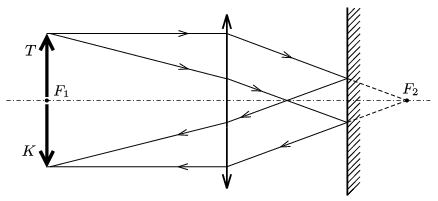
10. ábra

Fordított állású, a tárggyal megegyező nagyságú, valódi kép keletkezik a tárgy ,,helyén''. \(\displaystyle F_{1}=O_{\text{tükör}}\) tehát, és ez független attól, milyen \(\displaystyle \ell\) távolságra van a síktükör a lencsétől.

a) Anna 20 cm-re helyezte el a tükröt az f=30 cm fókusztávolságú lencse mögé. Hogyan határoznánk meg Anna helyében legegyszerűbben a leképező rendszer F^* fókuszpontjának a helyét? Úgy, hogy az optikai tengellyel párhuzamos fénynyalábot bocsátanánk a lencsére, és megnéznénk, hogy mi a ,,tartópontja'' annak a sugárnyalábnak, amely ebből a párhuzamos nyalábból keletkezik, miután megtörik a lencsén, visszaverődik a síktükrön, majd újta áthalad a lencsén (11. ábra). Biztosak lehetünk abban, hogy F^* helye már nemcsak f-től, hanem \(\displaystyle \ell\)-től is függeni fog.

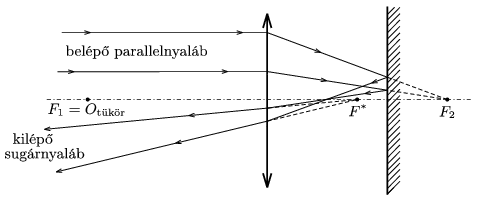
11. ábra

Kövessük Anna gondolatmenetét!

A belépő parallelnyaláb a lencse mögött 30 cm-re lévő F₂ fókuszpont felé tart, miután megtörik a lencsén. Ráesik a lencsétől 20 cm-re lévő síktükörre, s mivel a tükör mögött 10 cm-re lévő F₂ pont felé tartott, ezért a tükörről visszaverődve a tükör előtt 10 cm-re lévő ponton fog áthaladni. Ez a pont t=10 cm-re van a lencsétől; keressük meg egy ilyen távol lévő tárgy képét!

\(\displaystyle \frac{1}{10}+\frac{1}{k}=\frac{1}{30}, \)

amiből k=-15 cm adódik. Látszólagos kép keletkezik, ez azt jelenti, hogy a lencséből olyan sugárnyaláb fog kilépni, amelynek ,,tartópontja'' egy, a lencse mögött 15 cm-re levő pont. Ez tehát a leképező rendszer F^* fókuszpontja!

Annának tehát a helyettesítő homorú tükör egy újabb jellemző pontját sikerült megtalálnia. Mivel a homorú tükör fókuszpontja éppen a gömb sugarának közepén van, ezért a fókusztávolságot úgy is megkaphatja, hogy az F^* fókuszpont és a korábban már megtalált \(\displaystyle O_\text{tükör}\) geometriai középpont távolságát határozza meg:

\(\displaystyle f^*=F^*O_\text{tükör}=30~{\rm cm}+15~{\rm cm}=45~{\rm cm}. \)

Hová, a lencse hűlt helyétől mekkora x távolságra kell tenni ezt a homorú gömbtükröt? Mivel F^* 15 cm-re van attól a ponttól, ahol a lencse állt, ezért a keresett távolság (12. ábra):

x=15 cm+45 cm=60 cm.

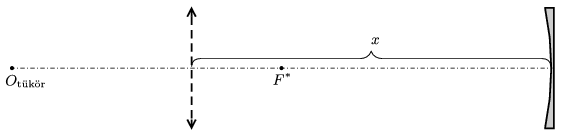
12. ábra

b) Balázs is követi Anna gondolatmenetét, de paraméteresen határozza meg a kérdezett mennyiségeket.

Az F^* fókuszpont helyének meghatározása: t=\(\displaystyle \ell\)-(f-\(\displaystyle \ell\))=2\(\displaystyle \ell\)-f, [9pt] <<\frac>>12\(\displaystyle \ell\)-f+<<\frac>>1k=<<\frac>>1f, <<\text>>ahonnan k=<<\frac>>(2\(\displaystyle \ell\)-f)f2\(\displaystyle \ell\)-2f<0. A keresett tükör fókusztávolsága:

\(\displaystyle f^*=f+\vert k\vert=f-k=\ldots=\frac{f^2}{2(f-\ell)\)0. ">

A homorú tükör távolsága a lencse helyétől:

\(\displaystyle x=2f^*-f=\ldots=\frac{f\ell}{f-\ell\)0. ">

c) Cecília felismerése: f>\(\displaystyle \ell\) kell legyen, mert a feladatban azt kellett megvizsgálni, hogy homorú gömbtükörrel lehet-e helyettesíteni a (lencse + síktükör) leképező rendszert. Ezen kívül azt is Cecíliának kell észrevennie, hogy Anna és Balázs megoldása csak a tárgytér meghatározott tartományára érvényes. Jelen esetben azokra a tárgypontokra, amelyek a lencsének a síktükörrel ellentétes oldalán helyezkednek el. Dehát ez természetesen teljesül, ha valódi tárgyat képez le az optikai rendszer.

Megjegyzés. A lencse + síktükör rendszer leképezése úgy is vizsgálható, hogy a lencsének és a lencse tükörképének, mint két lencséből álló lencserendszernek a leképezését követjük végig, majd a kapott képet visszatükrözzük a síktükörrel. Ezért is meglepő, hogy a leképezés végülis egyetlen homorú tükörrel helyettesíthető, hiszen egymástól távol elhelyezkedő két lencse leképezése sohase helyettesíthető egyetlen lencse adta képpel. A vékonylencse síkja helyett két fősík jelenik meg, s csak az ezektől mért t, k és f távolságokra lehet felírni a leképezési törvényt.

Nos, a mi esetünkben a két lencse fókusztávolsága egyenlő, ilyenkor a fősíkok is szimmetrikusan helyezkednek el, s amikor a szerkesztés végén a képet (és a képoldali fősíkot is) visszatükrözzük, a két fősík egybe fog esni! Az ide, a fősíkok közös helyére elhelyezett gömbtükörrel ekkor már helyettesíthető lesz a lencséből és a síktükörből álló rendszer.

A fősíkokkal történő leképezés nem középiskolai, hanem főiskolai, egyetemi tananyag; ennek ellenére volt olyan versenyző, aki ezt a gondolatmenetet próbálta meg követni. Hasonlóképpen egyetemi tananyag az úgynevezett ,,mátrixoptika'' is, amellyel Pálfalvi László mutatja meg e feladat megoldását a 179. oldalon.

Az eredményhirdetés

2007. november 30-án került sor az ünnepélyes eredményhirdetésre az Eötvös Loránd Tudományegyetem Ortvay Rudolfról elnevezett előadótermében.

Bevezetésként a Versenybizottság elnöke emlékezett meg Tolnai Jenőről, aki 100 évvel ezelőtt nyerte meg a Társulat tanulóversenyét, Neukomm Gyuláról, a KöMaL egykori főszerkesztőjéről, aki ötven éve hunyt el, és ebben az évben sikerült a sírját védetté nyilvánítani, Boros Jánosról, a Versenybizottság volt tagjáról, akinek éppen ezen a napon lett volna a születésnapja és Varga Istvánról, a csak nemrég elhunyt fizikatanárról, aki sziporkázó ötleteivel támogatta a Versenybizottság munkáját.

Ezután az 50 évvel ezelőtt, 1957-ben rendezett Eötvös-versenyt elevenítette fel. Bemutatta az akkori feladatokat és a díjazottak egykori fényképét is a KöMaL képarchívumából. Papp Kálmánt, a verseny 50 évvel ezelőtti nyertesét sajnos nem sikerült elérnie, és nem tudott eljönni Cserteg István sem, aki akkor a második helyezett volt. Mindketten villamosmérnökök lettek később. Nem így Szatmáry Zoltán, a harmadik helyezett piarista diák, aki Neukomm Gyula hathatós támogatásával tudott bekerülni az ELTE fizikus szakára 1957-ben. A KFKI kutatója, a műegyetemi tanreaktor Kossuth-díjas igazgatója személyesen idézte fel egyetemre kerülésének izgalmas történetét.

A 25 évvel ezelőtt díjazottak közül is csak egyetlen versenyző tudott eljönni: Károlyi Gyula, aki ma már egyetemi oktató, a KöMaL matematika szerkesztő bizottságának tagja. Csörgő Tamás, Erdős László és Tóth Gábor, az akkori első díjasok valamennyien hazai és külföldi kutatóintézetek, egyetemek sikeres kutatói. A KöMaL tehetségfejlesztő munkáját dicséri, hogy az 50 évvel ezelőtt díjazott mindhárom versenyző, a 25 évvel ezelőtt díjazott hat versenyző közül pedig öten voltak a KöMaL feladatmegoldói, és fényképük is megjelent a Lapokban, melyet most kivetítve láthatott és tapsolhatott meg a hálás közönség.

Ezután került sor a 2007. évi feladatok bemutatására, a helyes megoldások ismertetésére. Mindegyik megoldást kísérleti bemutató követte: az első két feladathoz Honyek Gyula, a harmadikhoz Radnai Gyula mutatott be érdekes kísérleteket. Az üveglapok közé felfutó víz, a meglepően jól égő kis izzó, valamint a lencse plusz síktükörrel és az ezeket helyettesítő gömbtükörrel egymás mellett előállított éles képek azokat is meggyőzték, akik esetleg kételkedtek volna a bemutatott megoldások helyességében. Szerencsére itt nem voltak ilyenek, - a közönség főleg a fizikát értő és szerető fiatalokból, tanáraikból és volt Eötvös-verseny nyertesekből állt. Itt volt a Társulat egész ,,vezérkara'', Kádár György főtitkár, Pákó Gyula, a középiskolai szakcsoport elnöke és Sólyom Jenő akadémikus, a társulat elnöke is, aki ezek után mosolyogva adta át a díjakat a verseny győzteseinek.

Első díjat és az ezzel együtt járó Eötvös-verseny érmet kapta a verseny 1. helyezettje: Werner Miklós, a BME hallgatója, aki az ELTE Apáczai Csere János Gyakorló Gimnáziumában érettségizett Flórik György tanítványaként. Ugyancsak első díjat kapott a 2. helyezett Kónya Gábor, az ELTE hallgatója, aki a Fazekas Mihály Fővárosi Gyakorló Gimnáziumban érettségizett Horváth Gábor tanítványaként.

Második díjat is két versenyző kapott: Eisenberger András, a Fazekas Mihály Fővárosi Gyakorló Gimnázium 12. évfolyamán Horváth Gábor tanítványa és Konczer József, a BME hallgatója, aki a szlovákiai Révkomárom Selye János Gimnáziumában érettségizett Hevesi Anikó és Szabó Endre tanítványaként.

Harmadik díjat nyert Szolnoki Lénárd, a Debreceni Református Kollégium Dóczy Gimnáziumának 12. osztályos tanulója, Tófalusi Péter tanítványa.

Dicséretet kapott a verseny 6-11. helyezettje, helyezésük szerinti sorrendben a következők: Kőrösi Márton, az ELTE hallgatója, aki a békéscsabai Szent-Györgyi Albert Gimnáziumban érettségizett Varga István tanítványaként; Almási Gábor, a pécsi Leöwey Klára Gimnázium 12. osztályos tanulója, Kotek László és Simon Péter tanítványa; Papp László, az ELTE hallgatója, aki a romániai Margitta O. Goga Nemzeti Kollégiumában érettségizett Bogdán Károly és Veres Zoltán tanítványaként; Roósz Gergő, a Szegedi Tudományegyetem hallgatója, aki a szegedi Radnóti Miklós Gimnáziumban érettségizett Mező Tamás és Mike János tanítványaként; Meszéna Balázs, az ELTE hallgatója, aki a Fazekas Mihály Fővárosi Gyakorló Gimnáziumban érettségizett és Takács Lajos tanítványa volt; Lovász László Miklós, aki ugyanennek a gimnáziumnak 12. osztályos diákja, Horváth Gábor tanítványa.

Az első díjjal 20 ezer forint, a másodikkal 15 ezer, a harmadikkal 10 ezer forint jutalom járt együtt, és még a dicséretet nyert versenyzők is kaptak 5 ezer forintos könyvutalványokat az ELFT, az INDOTEK Befektetési Zrt., valamint Gutai László (USA) által felajánlott támogatások jóvoltából. Mind a 11 kitüntetett versenyző megkapta Szatmáry Zoltán és Aszódi Attila Csernobil c. könyvét a Typotex Kiadótól. A versenyzők tanárai a Typotex, a Műszaki és a Vince kiadók könyveiből válogathattak a Matfund Alapítvány pártoló támogatásával.

Ezek után már csak a közös fénykép elkészítése volt hátra, amelyet Olvasóink a KöMaL hátsó borítóján tekinthetnek meg. A programot záró tapasztalatcsere-beszélgetéshez a Ramasoft Zrt. gondoskodott elegendő enni-innivalóról. A hangulat idén is jó volt: vidáman, felszabadultan tárgyalták a verseny tapasztalatait a régi és új versenyzők, tanárok az ország különböző részeiről, egyetemi tanárok Budapestről és Kolozsvárról. Gondolatban itt volt Béky Bence, nemrég még Eötvös-versenyen díjat nyert diák is, ma már tanulmányainak befejezéséhez közeledő mérnök-fizikus hallgató, aki Párizsból küldte üdvözletét egy beszédfelismerés témájú programról, amelyen a hazai egyetemi képzés keretében vesz részt. Aki pedig egyszer kedvet kapott a tanuláshoz, nem is tudja abbahagyni; ő most matematikából szeretne újabb diplomát szerezni. ,,Azt üzenem a versenyzőknek, tanuljanak, mert tanulni jó befektetés és tiszta öröm! Bár inkább nem is üzenek semmit, mert aki az Eötvös-verseny eredményhirdetésére bejutott, az ezt már úgyis tudja. Gratulálok nektek és további sok sikert kívánok!''

Radnai Gyula

Ehhez csatlakozik a Versenybizottság is. Bízzunk a lendület megmaradásában...