Surányi János professzor úrnak a Középiskolai Matematikai és Fizikai Lapok volt főszerkesztőjének és szerkesztőbizottsági elnökének a tiszteletére 80. születésnapja alkalmából barátai, tanítványai és tisztelői 1998. május 25-én az MTA Matematikai Kutató Intézetében ünnepi ülésszakot rendeztek. A most következő cikk az ott elhangzott előadás kibővített változata.
Binomiális együtthatók és teljes hatványok
Bevezetés
Régi, sokat vizsgált diofantikus problémák voltak a következők: egymás utáni egészek szorzata, illetve binomiális együttható mikor lehet teljes hatvány? Számos részeredmény után az első kérdést 1975-ben, a másodikat 1997-ben sikerült teljesen megválaszolni. A dolgozat első részében az első probléma történetének rövid áttekintését adjuk. A második részben részletesebben foglalkozunk a binomiális együtthatókkal kapcsolatos problémával és annak megoldásával. Végül a harmadik részben a két probléma egy közös általánosításáról és annak 1998-ban nyert megoldásáról számolunk be röviden.
1. Egymásra következő egész számok szorzata
A számelmélet egyik híres kérdése volt, hogy lehet-e egymásra következő pozitív egész számok szorzata teljes hatvány. Más megfogalmazásban: mik az
(1) n(n+1)...(n+k-1)=xl
diofantikus egyenlet pozitív egész megoldásai a k Az 1820-as évekből származik az a sejtés, hogy az (1) egyenletnek egyáltalán nincs megoldása. A sejtéssel
már a múlt században is sokan foglalkoztak. Számos speciális eredmény
született azokban az esetekben, amikor k értéke ,,kicsi'' és
l=2 vagy l=3. Az érdeklődő olvasó ezek ismertetését
megtalálhatja L. E. Dickson ,,History of the Theory
of Numbers'' című könyvének II. kötetében, a 679-680. oldalon (l. [1]).
1917-ben S. Narumi bebizonyította a sejtést a k 1939-ben Erdős Pál és O. Rigge egymástól
függetlenül bebizonyították a sejtést l=2-re. Bizonyításuk
meglehetősen komplikált, szellemes elemi okoskodásokon
alapult. Egyebek között felhasználták Sylvesternek azt a
tételét, hogy ha n>k P(n(n+1)...(n+k-1))>k.
Itt P(a) egy a>1 egész szám legnagyobb
prímosztóját jelöli.
1940-ben Erdős Pál és C. L. Siegel közösen
bebizonyították a sejtést minden elegendően nagy
k-ra. Bizonyításukban diofantikus approximációs módszereket
használtak, de magát a bizonyítást soha nem publikálták. 1955-ben
Erdős erre a tételre egy másik, elemi bizonyítást adott. Erdős
módszerét továbbfejlesztve, végül 1975-ben Erdős és
J. L. Selfridge a sejtést teljes általánosságban
igazolták.
1. Tétel. (Erdős P. és J. L.Selfridge [2].)
Az (1) egyenletnek nincs megoldása.
Érdekes megjegyezni, hogy a komplikált és igen szellemes elemi
bizonyítás jelentős mennyiségű numerikus számítást is igényelt. A
témakör részletesebb tárgyalását adja W. Narkiewicz
,,Classical problems in number theory'' című könyvében (l. [7]).
Az (1)
egyenlettel rokon diofantikus egyenlet
(2) ahol a megoldásokat
a k összefüggést felhasználva, valamint k-t és
n-1-et felcserélve a (2) egyenletre vonatkozó eredmények az
n A k=l=2 esetben az egyenlet
(n+1)n=2x2 alakra
hozható. Ekkor
vagy n=u2, n+1=2v2,
vagy n=2v2, n+1=u2,
ahol u, v pozitív egészek. Innen az
u2-2v2= Pell-egyenletekre jutunk, melyeknek végtelen sok u, v
pozitív egész megoldásuk van. Így ebben az esetben (2)-nek is végtelen sok megoldása van.
A k=3, l=2 esetet páratlan n-re
A. J. J. Meyl (1878), páros n-re
G. N. Watson (1919) intézte el. Eredményeikből
következik, hogy ebben az esetben (2) egyetlen
megoldása n=48, x=140, azaz
Erdős egy 1939-ben megjelent dolgozatában fogalmazta meg azt
a sejtést, hogy l>2 esetén a (2) egyenletnek
nincs megoldása. Ugyanebben a dolgozatban ezt az állítást az
l=3 és a k Az (1) egyenletre korábban alkalmazott elemi
módszere segítségével Erdős 1951-ben bebizonyította, hogy
k Az Erdős-Surányi könyv 1960-ban jelent meg
először. Élvezetes stílusa, bizonyításainak szépsége, a könyvben
felvetett sok nyitott probléma rendkívül népszerűvé tették a könyvet a
számelméletet kedvelők körében. A jelen dolgozat szerzője a könyv
hatására kezdett a 60-as évek elején, egyetemista korában az
Erdős-sejtés még nyitott k=2, 3 esetével foglalkozni. Első
publikációja is ezzel kapcsolatos eredményeket tartalmazott.
Az Erdős-Surányi könyv első kiadásának valamennyi példánya hamar
elfogyott a könyvesboltokban. 1996-ban jelent meg a könyv második,
kibővített kiadása (l. [3]). Ennek angol nyelvű
változata sajtó alatt van a Springer kiadónál.
Visszakanyarodva az Erdős-sejtéshez, 1951 után nyitott maradt a
k=2 és a k=3 eset. Kiderült, hogy Erdős elemi módszere a
k=2 és 3 esetre nem alkalmazható. Érdekes megjegyezni, hogy míg
az (1) egyenletben a k=2 és a k=3 esetek
bizonyultak a legkönnyebbeknek, a (2) egyenletnél a
helyzet ennek éppen az ellenkezője, a probléma 1996-ig ellenállt
minden próbálkozásnak. Ám szóljunk néhány szót az előzményekről,
amelyek később igen hasznosnak bizonyultak a sejtés teljes
általánosságban való bizonyítása során.
Erdős és Obláth eredményei következtében elég azzal az esettel
foglalkozni, amikor (2)-ben k=2 vagy 3 és
l>5 prímszám, amit a továbbiakban k-ról és l-ről
fel is tételezünk.
1963-ban sikerült bebizonyítanom, hogy ha a (2)
egyenlet k=2 esetén egy l>5 prímre nem megoldható, úgy
k=3-ra és a tekintett l-re csak akkor lehet megoldható,
ha
(3) 3l-1 Ez a kongruencia a kis Fermat-tétel szerint
(mod l2) helyett
(mod l) minden l>3 prímre teljesül. Tudjuk viszont,
hogy a 230-nál kisebb számok körében
(3) csak az l=11 és az
l=1 006 003 prímszámokra áll fenn. Így a nem túl nagy
l prímek esetén a k=3 esetet lényegében sikerült a
k=2 esetre visszavezetni.
R. Tijdeman 1976-ban az effektív Baker-módszer
felhasználásával bebizonyította, hogy a (2)
egyenletnek k=2 és k=3 esetén csak véges sok megoldása
lehet, és ezek a megoldások elvileg meghatározhatók. Tijdeman
bizonyítása egy olyan nagy felső korlátot szolgáltatott az n,
x, l ismeretlenekre, hogy a korlát alatti esetleges
megoldásokat még a mai modern számítógépekkel sem lehetne
megkeresni. A Baker-módszer egy élesebb változatát használva
N. Terai 1994-ben bebizonyította, hogy a (2) egyenletnek a k=2 és 3 esetekben csak akkor
lehet megoldása, ha l<4250.
A sejtés teljes bizonyításához az egyébként igen hatékony, mély és
széles körben alkalmazható Baker-módszer önmagában nem bizonyult
elegendőnek. Ehhez szükség volt a
(4) xl+yl=czl
általánosított Fermat-féle egyenlettel kapcsolatos néhány mély
eredményre. Itt l>5 prímszám, c Az olvasó számára bizonyára ismert, hogy Fermat híres sejtését
A. Wiles amerikai matematikus 1995-ben bebizonyította,
azaz megmutatta, hogy a (4) egyenletnek c=1
esetén nincs megoldása. Wiles (részben más matematikusok
közreműködésével) egy nehéz és mély módszert dolgozott ki a
Fermat-sejtés bizonyítására, amiről kiderült, hogy alkalmasan
továbbfejlesztve bizonyos más, 1-nél nagyobb c értékek esetén
is sikerrel alkalmazható. H. Darmon és L. Merel
egy 1997-ben megjelent dolgozatukban megmutatták, hogy a (4) egyenletnek c=2 esetén csak triviális
megoldásai vannak, amelyekre xyz= yl következne alkalmas 1-nél nagyobb y, z egészekkel,
ami a Darmon-Merel tétel szerint nem lehetséges.
Ezt követően sikerült az Erdős-sejtés bizonyításában az utolsó
lépést megtenni, a k=3 esetet is elintézni. A fentiekből
kitűnik, hogy ehhez tulajdonképpen már csupán egyetlen láncszem
hiányzott, az l=11 eset. Ehhez segítséget nyújtott
M. A. Bennett és
B. M. M. de Weger egy 1997-ben publikált
eredménye, mely szerint ha a, b, l pozitív
egészek, b>a>1 és 3 |axl-byl|=1
egyenletnek legfeljebb egy pozitív egész x, y
megoldása van. A fentieket felhasználva az 1997-ben megjelent [4] dolgozatomban megmutattam, hogy a (2)
egyenletnek a k=2 és k=3 esetben nincs megoldása, azaz
igaz a következő:
2. Tétel. (Erdős P., k A 2. Tételt a fenti formában publikáltam a [4]
dolgozatomban. Az eddigiekből világos, hogy a tétel a felsorolt
matematikusok által nyert részeredmények együtteséből született.
Erdős Pál rendszeres időközönként ellátogatott hozzánk
Debrecenbe. Halála előtt tervezte, hogy 1996. október elején ismét
meglátogat bennünket. A k=2 és k=3 esetekre a
bizonyítást 1996 szeptemberében, Erdős Pál halála után pár nappal
találtam. Úgy ismertük Őt, hogy biztosan örült volna a sejtése teljes
bizonyításának. A [4] cikket az Ő emlékének
dedikáltam.
Darmon és Merel, valamint Bennett és de Weger cikkei 1996-ban
még csak megjelenés alatt voltak, ám a szerzők voltak szívesek
kézirataikból egy-egy példányt rendelkezésemre bocsátani. És itt jön
egy érdekesség: a k=3 eset bizonyításához szükség volt a
fentebb ismertetett, 1963-as eredményemre. Ezt az eredményt a külföldi
kollégák nem ismerték. Gondolom azért, mert annak idején azt magyarul,
a Matematikai Lapokban publikáltam. Emiatt az angol nyelvű [4] dolgozatomban a k=3 esetre egy részletes,
teljes bizonyítást adtam, az 1963-as eredményem bizonyítását is
beépítve.
A k=3 eset bizonyításának főbb lépései a következők. Ha a
k=3 és l>5 prím esetben (2) megoldható
és 3|n, vagy 3|n+2, úgy könnyen belátható, hogy n=2wl, n+1=3vl, n+2=2lul
ahol n (5) 2(wl diofantikus egyenletrendszerek adódnak.
Itt szükség volt egy S. Lubelskitől és a jelen
szerzőtől származó tételre, mely szerint a (4)
egyenletből c>1 esetén (bizonyos technikai feltételek mellett)
következik, hogy ha x, y, z megoldás és
3|x-y (Lubelski, 1935) vagy 3|x+y (Győry,
1966), akkor szükségképpen teljesül a (3)
kongruencia. Ennek bizonyításához mély algebrai számelméleti
eszközökre volt szükség.
Az említett eredmény felhasználásával be lehet bizonyítani, hogy az
(5)-ben szereplő diofantikus egyenletrendszerek
akármelyikének a megoldhatóságából következik a (3)
kongruencia. Továbbá (5)-ből adódóan
|2wl-3vl|=1,
aminek v=w=1 megoldása. Ezért l<17 vagy
l>347 esetén Bennett és de Weger tétele szerint további
megoldás nem létezhet, azaz az (5) egyenletrendszerek
a v>1, w>1 feltételek mellett nem megoldhatók. A
fennmaradó 17 Az (1) és (2) egyenletek közös
általánosításaként tekintsük most a
(6) n(n+1)...(n+k-1)=bxl
egyenletet, ahol n, k, b, x, l
valamennyien pozitív egész ismeretlenek és k A (6) egyenlettel és annak további
általánosításaival (például a dolgozat végén szereplő (7) és (8)
egyenletekkel) sokan, közöttük Erdős Pál, T. N. Shorey,
R. Tijdeman, N. Saradha, Hajdú Lajos, Brindza Béla, Ruzsa
Imre és a szerző foglalkoztak.
Mint fentebb láttuk, a (6) egyenletnek a
k=b=l=2 esetben végtelen sok megoldása van.
Elég a (6) egyenlet azon
(n, k, b, x, l) megoldásaival foglalkozni,
amelyekre P(x)>k. Valóban, adott k-ra a (6) egyenletnek csak véges sok P(x) Példa. Könnyen ellenőrizhető, hogy p(2)=3 és p(3)=5. Ezért k=2, 3 esetén
(6) összes, P(x)
(1, 2, 2, 1, l Az Erdős-Selfridge tétel bizonyításának módszerét továbbfejlesztve
N. Saradha egy 1997-ben megjelent dolgozatában
bebizonyította, hogy k A Wiles-módszer egy változatával K. A. Ribet
1997-ben megmutatta, hogy a (4) egyenletnek nincs
megoldása, amennyiben c a 2-nek 1-nél nagyobb és l-nél
kisebb kitevőjű hatványa. A Darmon-Merel-tétel és a Ribet-tétel
felhasználásával a szerzőnek [5] újabban sikerült
Saradha eredményének megfelelőjét k=2 és k=3-ra is
igazolnia. A következő, [5]-ben ilyen formában
publikált tétel a (6) egyenlet teljes megoldását
szolgáltatja a P(x)>k feltétel mellett.
3. Tétel. (N. Saradha, k Most megmutatjuk, hogy a 3. Tételből levezethető mind az
1. Tétel, mind pedig a 2. Tétel.
Először tekintsük az (1) egyenletet, s tegyük fel,
hogy (n, k, x, l) megoldása (1)-nek. A k=l=2 eset nyilván nem
lehetséges. Továbbá a 3. Tétel miatt P(x)>k
sem teljesülhet. Ha viszont P(x) Ezután tekintsük a (2) egyenlet egy
(n, k, x, l) megoldását. A (2)
egyenlet
n(n+1)...(n+k-1)=bxl
alakba írható, ahol b a k! legnagyobb l-edik
hatványmentes osztója. Feltevés szerint n Az (1), (2) és (6)
egyenletek további általánosításai a
(7) n(n+d)...(n+(k-1)d)=xl
és a
(8) n(n+d)...(n+(k-1)d)=bxl
egyenletek, ahol n, d, k, b, x,
l pozitív egész ismeretlenek, k [1] L. E. Dickson, History of the Theory of
Numbers, 2. kiadás, Chelsea Publ. Comp., New York, 1971.
[2] P. Erdős and J. L. Selfridge, The
product of consecutive integers is never a power, Illinois
J. Math. 19 (1975), 292-301.
[3] Erdős Pál és Surányi János,
Válogatott fejezetek a számelméletből, Tankönyvkiadó Vállalat,
Budapest, 1960. Második, kibővített kiadás: Polygon, Szeged, 1996.
[4] K. Győry, On the diophantine equation [5] K. Győry, On the diophantine equation
n(n+1)...(n+k-1)=bxl, Acta Arith., 83 (1998), 87-92.
[6] K. Győry, Power values of products of
consecutive integers and binomial coefficients, in: ,,Number Theory
and Its Applications'' Kluwer Acad. Publ., megjelenés alatt.
[7] W. Narkiewicz, Classical Problems in Number
Theory, Polish Scientific Publ., Warszawa, 1986.
 2, x
2, x 2,
l
2,
l 2 feltételek mellett? A
k=2 esetben nyilván nincs megoldás. A probléma
C. Goldbachig nyúlik vissza, aki 1724-ben egy
D. Bernoullihoz írt levélben megjegyezte, hogy az (1) egyenletnek k=3, l=2 esetén nincs
megoldása. Valóban, ha volna ilyen megoldás, úgy a bal oldalt
(n+1)[(n+1)2-1] alakba
írva az következne, hogy (n+1)2-1 négyzetszám, ami nem lehetséges. Hasonló
okoskodás alkalmazható a k=3, l>2 esetre is.
2 feltételek mellett? A
k=2 esetben nyilván nincs megoldás. A probléma
C. Goldbachig nyúlik vissza, aki 1724-ben egy
D. Bernoullihoz írt levélben megjegyezte, hogy az (1) egyenletnek k=3, l=2 esetén nincs
megoldása. Valóban, ha volna ilyen megoldás, úgy a bal oldalt
(n+1)[(n+1)2-1] alakba
írva az következne, hogy (n+1)2-1 négyzetszám, ami nem lehetséges. Hasonló
okoskodás alkalmazható a k=3, l>2 esetre is.
 202, l=2 értékekre, Szekeres
György pedig a 30-as években megmutatta, hogy (1)-nek nincs olyan megoldása, melyre k
202, l=2 értékekre, Szekeres
György pedig a 30-as években megmutatta, hogy (1)-nek nincs olyan megoldása, melyre k 8.
8.
 2
egész számok, úgy
2
egész számok, úgy
2. Binomiális együtthatók
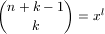 ,
,
 2, n
2, n k+1, x
k+1, x 2,
l
2,
l 2 tulajdonságú egész számok
körében keressük. Itt az n
2 tulajdonságú egész számok
körében keressük. Itt az n k+1
feltétel lényegében nem jelent megszorítást. Valóban, az
k+1
feltétel lényegében nem jelent megszorítást. Valóban, az
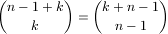
 k esetre is alkalmazhatók.
k esetre is alkalmazhatók.
 1
1
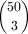 =1402.
=1402. 2l esetekben igazolta. Az l=4, 5
eseteket Obláth Richárdnak sikerült elintéznie 1948-ban.
2l esetekben igazolta. Az l=4, 5
eseteket Obláth Richárdnak sikerült elintéznie 1948-ban.
 4 esetén a (2)
egyenletnek nincs megoldása. A bizonyítás igen szép és szellemes,
magyar nyelven is elérhető Erdős Pál és Surányi János
,,Válogatott fejezetek a számelméletből'' című könyvében (l. [3]).
4 esetén a (2)
egyenletnek nincs megoldása. A bizonyítás igen szép és szellemes,
magyar nyelven is elérhető Erdős Pál és Surányi János
,,Válogatott fejezetek a számelméletből'' című könyvében (l. [3]).
 1 (mod l2).
1 (mod l2).
 1 egész szám, x, y, z pedig
0-tól különböző, relatív prím egész ismeretlenek.
1 egész szám, x, y, z pedig
0-tól különböző, relatív prím egész ismeretlenek.
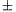 1 teljesül. Bár Darmon ás Merel dolgozatukban nem
foglalkoztak a (2) egyenletre vonatkozó
Erdős-sejtéssel (talán nem is ismerték azt), eredményükből egyszerűen
következik, hogy (2) a k=2 esetben nem
megoldható. Valóban, ha (2)-nek k=2 mellett
volna megoldása, úgy n=yl, n+1=2zl vagy n=2zl, n+1=yl, azaz
1 teljesül. Bár Darmon ás Merel dolgozatukban nem
foglalkoztak a (2) egyenletre vonatkozó
Erdős-sejtéssel (talán nem is ismerték azt), eredményükből egyszerűen
következik, hogy (2) a k=2 esetben nem
megoldható. Valóban, ha (2)-nek k=2 mellett
volna megoldása, úgy n=yl, n+1=2zl vagy n=2zl, n+1=yl, azaz
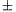 1=2zl
1=2zl
 l<17 vagy l>347, akkor az
l<17 vagy l>347, akkor az
 4 eset; H. Darmon és L. Merel, k=2 eset;
Győry K., k=3 eset.) A k=l=2 esettől
eltekintve a (2) egyenlet egyetlen megoldása
(n, k, x, l)=(48, 3, 140, 2),
azaz
4 eset; H. Darmon és L. Merel, k=2 eset;
Győry K., k=3 eset.) A k=l=2 esettől
eltekintve a (2) egyenlet egyetlen megoldása
(n, k, x, l)=(48, 3, 140, 2),
azaz 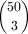 =1402.
=1402.
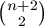 , illetve
, illetve 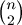 teljes l-edik hatvány, ami a Darmon-Merel
tétel miatt nem lehet. Maradt a 3|n+1 eset, amikor
teljes l-edik hatvány, ami a Darmon-Merel
tétel miatt nem lehet. Maradt a 3|n+1 eset, amikor
vagy n=2lul, n+1=3vl, n+2=2wl,
 1 és v>1,
w>1 egészek. Innen az
1 és v>1,
w>1 egészek. Innen az
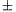 1)=3vl
1)=3vl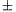 1=(2u)l
1=(2u)l
 l
l 347 esetekben a (3) kongruencia
nem teljesül, így készen vagyunk. Megjegyezzük, hogy itt használhattuk
volna Terai eredményét is, ebben az esetben Bennett és de Weger
tételét elég az l=11 esetre alkalmazni.
347 esetekben a (3) kongruencia
nem teljesül, így készen vagyunk. Megjegyezzük, hogy itt használhattuk
volna Terai eredményét is, ebben az esetben Bennett és de Weger
tételét elég az l=11 esetre alkalmazni.
3. Az (1) és (2)
egyenletek egy közös általánosítása
 2, l
2, l 2,
P(b)
2,
P(b) k, b
l-edik hatványmentes. Amennyiben b=1, úgy ez éppen az (1) egyenlet, míg ha b a k! l-edik
hatványmentes része, úgy a (2) egyenletet kapjuk. Azt
a feltételt, hogy b l-edik hatványmentes, elejthetnénk. Viszont
ezen feltétel mellett a (6) jobb oldalának
bxl alakban való
felírása egyértelművé válik, ami később hasznosnak fog bizonyulni.
k, b
l-edik hatványmentes. Amennyiben b=1, úgy ez éppen az (1) egyenlet, míg ha b a k! l-edik
hatványmentes része, úgy a (2) egyenletet kapjuk. Azt
a feltételt, hogy b l-edik hatványmentes, elejthetnénk. Viszont
ezen feltétel mellett a (6) jobb oldalának
bxl alakban való
felírása egyértelművé válik, ami később hasznosnak fog bizonyulni.
 k tulajdonságú megoldása van, és
mindezek könnyen meghatározhatók. Jelöljük ugyanis p(k)-val a legkisebb olyan prímszámot,
melyre p(k)>k. Sylvester fentebb idézett
tételének következménye, hogy P(x)
k tulajdonságú megoldása van, és
mindezek könnyen meghatározhatók. Jelöljük ugyanis p(k)-val a legkisebb olyan prímszámot,
melyre p(k)>k. Sylvester fentebb idézett
tételének következménye, hogy P(x) k mellett
(n, k, b, x, l) akkor és csak akkor
megoldása (6)-nak, ha n
k mellett
(n, k, b, x, l) akkor és csak akkor
megoldása (6)-nak, ha n {1, 2, ..., p(k)-k} . Tehát n és így
b, x, l tényleg könnyen meghatározható. Vegyük
észre, hogy n=1 minden k-ra megoldása (6)-nak, k! mindig felírható bxl alakban a kívánt tulajdonsággal.
{1, 2, ..., p(k)-k} . Tehát n és így
b, x, l tényleg könnyen meghatározható. Vegyük
észre, hogy n=1 minden k-ra megoldása (6)-nak, k! mindig felírható bxl alakban a kívánt tulajdonsággal.
 k tulajdonságú
(n, k, b, x, l) megoldásai:
k tulajdonságú
(n, k, b, x, l) megoldásai:
 2), (1, 3,
6, 1, l
2), (1, 3,
6, 1, l  2),
2),
(2, 3, 24,
1, l  4), (2, 3,
6, 2, 2), (2, 3,
3, 2, 3).
4), (2, 3,
6, 2, 2), (2, 3,
3, 2, 3).
 4 esetén
a (6) egyenletnek nincs olyan megoldása, amelyre
P(x)>k. A bizonyítás a k=2 és 3 esetekre
nem alkalmazható.
4 esetén
a (6) egyenletnek nincs olyan megoldása, amelyre
P(x)>k. A bizonyítás a k=2 és 3 esetekre
nem alkalmazható.
 4 eset; Győry K., k
4 eset; Győry K., k 3 eset). A k=b=l=2 esettől
eltekintve (n, k, b, x, l)=(48,
3, 6, 140, 2), azaz
48.49.50=6.1402 a (6) egyenlet
egyetlen olyan megoldása, melyre P(x)>k.
3 eset). A k=b=l=2 esettől
eltekintve (n, k, b, x, l)=(48,
3, 6, 140, 2), azaz
48.49.50=6.1402 a (6) egyenlet
egyetlen olyan megoldása, melyre P(x)>k.
 k, úgy Sylvester tétele szerint n
k, úgy Sylvester tétele szerint n k, azaz n
k, azaz n
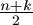 . Továbbá Csebisev
tétele következtében létezik olyan p prímszám, amelyre
. Továbbá Csebisev
tétele következtében létezik olyan p prímszám, amelyre 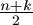
 p
p n+k-1. Ebből következik, hogy
p-nek csupán az első hatványa lehet osztója
n(n+1)...(n+k-1)-nek, ami (1) miatt nem lehetséges. Ezzel az 1. Tételt
levezettük a 3. Tételből.
n+k-1. Ebből következik, hogy
p-nek csupán az első hatványa lehet osztója
n(n+1)...(n+k-1)-nek, ami (1) miatt nem lehetséges. Ezzel az 1. Tételt
levezettük a 3. Tételből.
 k+1, ezért Sylvester tételét alkalmazva
P(x)>k adódik. Ekkor viszont a 2. Tétel már
azonnal következik a 3. Tételből.
k+1, ezért Sylvester tételét alkalmazva
P(x)>k adódik. Ekkor viszont a 2. Tétel már
azonnal következik a 3. Tételből.
 3, x
3, x 2,
l
2,
l 2, (n, d )=1 és
P(b)
2, (n, d )=1 és
P(b) k. Mint
említettük, ezekkel az egyenletekkel is sokan foglalkoztak, sok
érdekes eredményt publikáltak. Ezekről az eredményekről az érdeklődő
olvasó áttekintést nyerhet a [7], [9],
[8], [6] munkákból. Azonban
ellentétben az (1), (2) és (6) egyenletekkel, amelyeknek teljes megoldását ismerjük,
a (7) és (8) egyenletekkel
kapcsolatban eddig csupán részeredmények születtek.
k. Mint
említettük, ezekkel az egyenletekkel is sokan foglalkoztak, sok
érdekes eredményt publikáltak. Ezekről az eredményekről az érdeklődő
olvasó áttekintést nyerhet a [7], [9],
[8], [6] munkákból. Azonban
ellentétben az (1), (2) és (6) egyenletekkel, amelyeknek teljes megoldását ismerjük,
a (7) és (8) egyenletekkel
kapcsolatban eddig csupán részeredmények születtek.
Irodalom
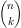 =xl, Acta Arith., 80 (1997), 289-295.
=xl, Acta Arith., 80 (1997), 289-295.

