Az A. 385. feladat (2005. november)

A. 385. Legyen $\alpha$ pozitív valós szám. Határozzuk meg az összes, nemnegatív számokból álló a₁,a₂,... sorozatot, amelynek összege, $S= \sum_{k=1}^\infty a_k$ véges és tetszőleges n pozitív egész esetén

$\sum_{k=1}^\infty a_{kn} = \frac{S}{n^\alpha}.$

Német versenyfeladat

(5 pont)

A beküldési határidő 2005. december 15-én LEJÁRT.

Megoldásvázlat. Felhasználjuk azt az ismert tételt, hogy a $\prod_p\left(1-\frac1{p^\alpha}\right)$ végtelen szorzat, ami a prímeken megy végig, határértéke 0, ha $\alpha$ $\le$ 1, és pozitív, ha $\alpha$ >1.

Vegyük az első n prímet: p₁,...,p_n, és szitáljuk ki az ezekkel osztható indexeket. Az eredeti sorozatból hagyjuk el azokat a tagokat, amelyek indexe osztható az egyik kiválasztott prímmel; adjuk hozzá azokat, amelyek indexe két kiválasztott prímmel osztható stb. A végén azok a tagok maradnak meg, amelyek indexe p₁,...,p_n egyikével sem osztható:

$\sum_{p_1,\dots,p_n\not| k} a_k = \prod_{k=1}^n\left(1-\frac1{p_k^\alpha}\right) \cdot S.$

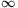Ha n $\to$ $\infty$ , akkor a baloldal a₁-hez tart, mert az összes többi tagot szép sorban kiszitáljuk.

Ha $\alpha$ $\le$ 1, akkor a jobboldal 0-hoz tart, tehát a₁=0. Ha ugyanezt rögzített l pozitív egészre az a_kl sorozattal játsszuk el, akkor azt kapjuk, hogy a_l=0.

Ha $\alpha$ >1, akkor a jobboldal konvergens, határértéke $c_\alpha\cdot S$ . Hasonlóan $a_l=\frac{c_\alpha S}{l^\alpha}$ .

Összefoglalva, $\alpha$ $\le$ 1 esetén csak a konstans 0 sorozat megoldás, $\alpha$ >1 esetén pedig az összes $a_k=\frac{c}{k^\alpha}$ alakú sorozat.

Statisztika:

9 dolgozat érkezett.

5 pontot kapott: Erdélyi Márton, Nagy 224 Csaba, Paulin Roland.

4 pontot kapott: Gyenizse Gergő, Hujter Bálint, Kónya 495 Gábor.

3 pontot kapott: 1 versenyző.

2 pontot kapott: 2 versenyző.

A KöMaL 2005. novemberi matematika feladatai

9 dolgozat érkezett.
5 pontot kapott:	Erdélyi Márton, Nagy 224 Csaba, Paulin Roland.
4 pontot kapott:	Gyenizse Gergő, Hujter Bálint, Kónya 495 Gábor.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	2 versenyző.

Már regisztráltál?
Új vendég vagy?