Az A. 404. feladat (2006. szeptember)

A. 404. Egy szabályos 2n-szög csúcsai . Egy V_iV_j átlót nevezzünk párosnak, ha i és j azonos paritású.

Bontsuk a sokszöget tetszőleges módon háromszögekre 2n-3 egymást nem metsző átló megrajzolásával. A felbontással a következő műveletet végezhetjük: kiválasztunk két csúcsot, V_i-t és V_j-t, amelyek vagy szomszédosak, vagy pedig egy megrajzolt átló köti össze őket, majd a V_iV_j egyenes egyik oldalán az összes, a felbontásban szereplő átlót kicseréljük a V_iV_j szakasz felező merőlegesére vonatkozó tükörképére az ábra szerint.

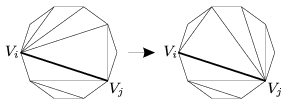
Bizonyítsuk be, hogy tetszőleges felbontásból kiindulva, ilyen lépésekkel elérhetjük, hogy minden páros átló páros sorszámú csúcsokat kössön össze.

A 47. Nemzetközi Matematikai Diákolimpia 2. feladata nyomán

(5 pont)

A beküldési határidő 2006. október 16-án LEJÁRT.

Statisztika:

21 dolgozat érkezett.
5 pontot kapott:	Dobribán Edgár, Gyürke Csaba, Hujter Bálint, Károlyi Márton, Kisfaludi-Bak Sándor, Korándi Dániel, Kornis Kristóf, Lovász László Miklós, Nagy 224 Csaba, Nagy 235 János, Nagy 314 Dániel, Szűcs 003 Gábor, Tomon István, Varga 171 László.
4 pontot kapott:	Dudás László, Fischer Richárd.
3 pontot kapott:	2 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2006. szeptemberi matematika feladatai