Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány

Már regisztráltál?
Új vendég vagy?

Az A. 468. feladat (2008. december)

A. 468. Adott két háromszög. Az oldalaik a, b, c, illetve A, B, C; területük t, illetve T. Igazoljuk, hogy

-a²A²+a²B²+a²C²+b²A²-b²B²+b²C²+c²A²+c²B²-c²C² $\ge$ 16tT.

(5 pont)

A beküldési határidő 2009. január 15-én LEJÁRT.

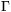Megoldás. Legyen $\gamma$ és $\Gamma$ a két háromszögben a c, illetve C oldallal szemközti szög.

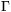A koszinusztétel szerint a²+b²-c²=2abcos $\gamma$ és A²+B²-C²=2ABsin $\Gamma$ ; a két terület pedig $t=\frac12ab\sin\gamma$ és $T=\frac12AB\sin\Gamma$ . Ezeket behelyettesítve,

-a²A²+a²B²+a²C²+b²A²-b²B²+b²C²+c²A²+c²B²-c²C²-16tT=

=2a²B²+2A²b²-(a²+b²-c²)(A²+B²-C²)-16tT=

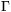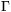=2a²B²+2A²b²-4abABcos $\gamma$ cos $\Gamma$ -4abABsin $\gamma$ sin $\Gamma$ =

=2(aB-Ab)²+4abAB(1-cos ( 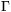$\gamma$ - $\Gamma$ )) $\ge$ 0.

Statisztika:

12 dolgozat érkezett.

5 pontot kapott: Blázsik Zoltán, Bodor Bertalan, Éles András, Márkus Bence, Nagy 235 János, Nagy 648 Donát, Somogyi Ákos, Tomon István, Tossenberger Anna, Varga 171 László, Wolosz János.

4 pontot kapott: Backhausz Tibor.

A KöMaL 2008. decemberi matematika feladatai

12 dolgozat érkezett.
5 pontot kapott:	Blázsik Zoltán, Bodor Bertalan, Éles András, Márkus Bence, Nagy 235 János, Nagy 648 Donát, Somogyi Ákos, Tomon István, Tossenberger Anna, Varga 171 László, Wolosz János.
4 pontot kapott:	Backhausz Tibor.