Az A. 480. feladat (2009. április)

A. 480. Tegyük fel, hogy p(z) olyan n-edfokú, komplex együtthatós polinom, melynek minden (komplex) gyöke egységnyi abszolút értékű. Mutassuk meg, hogy tetszőleges c $\ge$ 0 valós számra a

2z(z-1)p'(z)+((c-n)z+(c+n))p(z)

polinom gyökei is egységnyi abszolút értékűek.

(5 pont)

A beküldési határidő 2009. május 15-én LEJÁRT.

I. megoldás. Legyen

$p(z) = a_nz^n + a_{n-1}z^{n-1} + \ldots + a_1z + a_0,$

és

q(z)=2z(z-1)p'(z)+((c-n)z+(c+n))p(z).

Tegyük fel, hogy p(z)-nek összesen k különböző komplex gyöke van: $r_1=e^{ix_1},\ldots,r_k=e^{ix_k}$ , ahol $0\le x_1<\ldots<x_k<2\pi$ . A gyökök multiplicitásai legyenek rendre $m_1,\ldots,m_k$ ; a polinom gyöktényezős alakja tehát

$p(z) = a_n\prod_{\ell=1}^k(z-r_\ell)^{m_\ell}.$

Mivel a p polinom n-edfokú, $m_1+\ldots+m_k=n$ .

Minden egyes 1 $\le$ $\ell$ $\le$ k-ra a $(z-r_\ell)^{m_\ell-1}$ polinom osztója p-nek és a p'-nek, és velük együtt q-nak is. Ezért a q polinomnak már ismerjük (multiplicitással számolva) n-k gyökét. Sőt, ha a gyökök között szerepel az 1 (azaz r₀=1 és x₁=0), akkor eggyel több gyököt is ismerünk, mert (z-r₁)^m₁=(z-1)(z-r₁)^m₁-1 is osztója q-nak. A továbbiakban nevezzűk q-nak ezeket a gyökeit ,,triviális'' gyököknek; a triviális gyökök száma tehát legalább n-k+1 ha x₁=0, illetve legalább n-k ha x₁>0.

A továbblépéshez a következő azonosságokra lesz szükségünk:

$\frac{p'(z)}{p(z)} = \sum_{\ell=1}^k \frac{m_\ell}{z-r_\ell}$

(1)

$\frac{e^{iu}+e^{iv}}{e^{iu}-e^{iv}} = -i \ctg\frac{u-v}2$

(2)

Az (1) a differenciálási szabályok egyszerű és jól ismert következménye. A (2) bizonyításához bővítsük a törtet $e^{-i\frac{u+v}2}$ -vel:

$\frac{e^{iu}+e^{iv}}{e^{iu}-e^{iv}} = \frac{(e^{iu}+e^{iv})e^{-i\frac{u+v}2}}{(e^{iu}-e^{iv})e^{-i\frac{u+v}2}} = \frac{e^{i\frac{u-v}2+}+e^{-i\frac{u-v}2}}{e^{i\frac{u-v}2+}-e^{-i\frac{u-v}2}} = \frac{2\cos\frac{u-v}2}{2i\sin\frac{u-v}2} = -i \ctg\frac{u-v}2.$

Ezeket felhasználva,

$q(z) = (z-1)p(z)\left(2z\frac{p'(z)}{p(z)}+\frac{(c-n)z+(c+n)}{z-1}\right) = (z-1)p(z) \left(2z\sum_{\ell=1}^k\frac{m_\ell}{z-r_\ell} -n +c\frac{z+1}{z-1} \right) =$

$= (z-1)p(z) \left(\sum_{\ell=1}^k m_\ell\left(\frac{2z}{z-r_\ell}-1\right) + c\frac{z+1}{z-1} \right) = (z-1)p(z) \left(\sum_{\ell=1}^k m_\ell\frac{z+r_\ell}{z-r_\ell} +c\frac{z+1}{z-1} \right)$

(3)

és

$q(e^{it}) = (e^{it}-1)p(e^{it}) \left(\sum_{\ell=1}^k m_\ell\frac{e^{it}+e^{ix_\ell}}{e^{it}-e^{ix_\ell}} +c\frac{e^{it}+e^0}{e^{it}-e^0} \right) =$

$= -i (e^{it}-1)p(e^{it}) \left(\sum_{\ell=1}^k m_\ell \cdot \ctg\frac{t-x_\ell}2 + c \cdot \ctg\frac{t}2 \right).$

(4)

Vizsgáljuk most --- valós t értékekre --- az

$f(t) = \sum_{\ell=1}^k m_\ell \cdot\ctg\frac{t-x_\ell}2 + c\cdot\ctg\frac{t}2$

függvényt. A függvény nem értelmes az $x_\ell+2j\pi$ alakú helyeken, továbbá c>0 esetén a 2j $\pi$ alakú helyeken. Ezekben a pontokban, ,,pólusokban'' a bal- illetve jobboldai határértéke -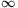 $\infty$ , illetve + 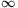$\infty$ , a közbülső intervallumokban a függvény folytonos, és az értéke tisztán valós

A Bolzano-tétel miatt az f függvény bármely két szomszédos pólus között felveszi a 0-t. Ha pedig valamely $\xi$ valós számra f( $\xi$ )=0, akkor (4) miatt az $e^{i\xi}$ komplex szám gyöke a q polinomnak, ez a gyök egységnyi abszolút értékű, és nem szerepel a ,,triviális'' gyökök között. Nevezzük az így talált gyököket q ,,nemtriviális'' gyökeinek. A nemtriviális gyökök száma (legalább) k vagy k+1 attól függően, hogy f-nek hány pólusa van egy perióduson.

A továbbiakban négy esetet különöztetünk meg c és x₁ értékétől függően.

1. eset: x>0, c>0. Az f függvénynek k+1 pólusa van: a 0 és az $x_1,\ldots,x_k$ számok. Az q-nak tehát legalább k+1 nemtriviális gyöke van az egységkörön. A triviális gyökökkel együtt ez (legalább) n+1 darab.

2. eset: x₁=0, c>0. A függvénynek k pólusa van: $x_1=0,x_2,\ldots,x_k$ . A nemtriviális gyökök száma tehát k. Mivel r₁=1, a triviális gyökök száma (legalább) n-k+1. A kétféle gyökből tehát összesen legalább n+1 darabot találtunk.

3. eset: x₁=0, c=0. Ha c=0, akkor a függvényből hiányzik a $c\cdot\ctg\frac{t}2$ tag. A pólusok, illetve a nemtriviális gyökök száma tehát k. Ha x₁=0, akkor a triviális gyökök száma legalább n-k+1, összesen legalább n+1.

4. eset: x₁>0, c=0. Az előző esethez hasonlóan a nemtriviális gyökök száma k, a triviális gyökök száma pedig n-k. A triviális gyökökön kívül q-nak az 1 is gyöke, mert

q(z)=2z(z-1)p'(z)+(-nz+n)p(z)=(z-1)(2zp'(z)-np(z)).

Ha az 1 szerepel a nemtriviális gyökök között, akkor a $\frac{q(z)}{z-1}$ polinomnak is gyöke, tehát legalább kétszeres gyök. Ez ismét csak n+1 gyök az egységgyökön.

Mindegyik esetben megtaláltuk q-nak legalább n+1 gyökét az egységkörön. Mivel q foka n+1, ez azt jelenti, hogy q-nak minden gyöke az egységkörön van.

Megjegyzés. A q(z) polinomban a fő együttható (c+n)a_n, a konstans tag (c+n)a₀. A Viéte-formulákból láthatjuk, hogy q gyökeinek szorzata egységnyi abszolút értékű. Ezért elég q-nak n gyökét megtalálnunk az eségkörön, és elkerülhetjük a négyféle eset szétválasztását.

II. megoldás. Tekintsük ismét a (3) egyenletet:

$\frac{q(z)}{(z-1)p(z)} = \sum_{\ell=1}^k m_\ell\frac{z+r_\ell}{z-r_\ell} +c\frac{z+1}{z-1}.$

(3')

Tetszőleges különböző z és $\alpha$ komplex számokra

$\mathrm{Re} \frac{z+\alpha}{z-\alpha} = \mathrm{Re} \frac{(z+\alpha)(\overline{z}-\overline{\alpha})}{|z-\alpha|^2} = \frac{|z|^2-|\alpha|^2+\mathrm{Re}(\overline{z}\alpha-z\overline{\alpha})}{|z-\alpha|^2} = \frac{|z|^2-|\alpha|^2}{|z-\alpha|^2}.$

(5)

Az (3) és (5) összefüggéseket összevetve láthatjuk, hogy $\mathrm{Re}\frac{q(z)}{(z-1)p(z)}$ mindig pozitív, ha |z|>1, és mindig negatív, ha |z|<1.

2. megjegyzés. A feladat kapcsolódik az 1995. évi IMC 2/3. feladatához.

Statisztika:

3 dolgozat érkezett.

5 pontot kapott: Nagy 235 János, Tomon István.

0 pontot kapott: 1 versenyző.

A KöMaL 2009. áprilisi matematika feladatai

3 dolgozat érkezett.
5 pontot kapott:	Nagy 235 János, Tomon István.
0 pontot kapott:	1 versenyző.

Már regisztráltál?
Új vendég vagy?