Az A. 552. feladat (2012. január)

A. 552. Bizonyítsuk be, hogy nemnegatív valós számok tetszőleges $a_1,a_2,\ldots$ sorozatához és $\varepsilon$ >0 számhoz végtelen sok olyan n pozitív egész létezik, amire

$n^2 \big(4a_n(1-a_{n-1})-1 \big) \le \frac14+\varepsilon.$

Schweitzer-verseny, 2011 alapján

(5 pont)

A beküldési határidő 2012. február 10-én LEJÁRT.

Megoldás. Tegyük fel indirekten, hogy a feladat állításával elentétben mégis van egy olyan $a_1,a_2,\ldots$ sorozat és $\varepsilon$ >0, amire

$n^2 \big(4a_n(1-a_{n-1})-1 \big) > \frac14+\varepsilon.$

(1)

teljesül véges sok n index kivételével. (Ezt úgy is mondhatjuk, hogy van egy olyan n₀ index, hogy (1) igaz minden n>n₀ esetén.) Az (1) egyszerű következménye, hogy

4a_n(1-a_n-1)>1;

(2)

ebből következik, hogy a_n>0 és a_n-1<1. Továbbá, a számtani és mértani közepek közötti egyenlőtlenségből

$1 < 2\sqrt{a_n(1-a_{n-1})} \le a_n + (1-a_{n-1}),$

vagyis a_n>a_n-1; a sorozat az n₀ indextől kezdve szigorúan monoton nő.

A monotonitás és a korlátosság miatt a sorozat konvergens. Megmutatjuk, hogy a határérték csak az $\frac12$ lehet. Legyen $A=\lim a_n$ ; ekkor (2)-re a határátmenetet alkalmazva

$4A(1-A) = \lim\big(4a_n(1-a_{n-1})\big) \ge 1$

(2A-1)² $\le$ 0,

ami csak $A=\frac12$ esetén lehetséges. Tehát az (a_n) sorozat az $\frac12$ -hez tart.

Legyen $x_n=\frac12-a_n$ . Ez a sorozat az n₀ indextől kezdve szigorúan monoton csökken, és 0-hoz tart. Az (1) egyenlőtlenséget átírva, n>n₀ esetén

$\frac{\frac14+\varepsilon}{n^2} < 4a_n(1-a_{n-1})-1 = 4\left(\frac12-x_n\right)\left(\frac12+x_{n-1}\right) - 1 = 2(x_{n-1}-x_n)-4x_{n-1}x_n$

$x_{n-1}-x_n > \frac{\frac14+\varepsilon}{2n^2} + 2x_{n-1}x_n > \frac1{8n^2}.$

(3)

A (3)-at összegezve, n>n₀ esetén például a következő alsó becslést kaphatjuk x_n-re:

$x_n = \sum_{i=n+1}^\infty (x_{i-1}-x_i) > \sum_{i=n+1}^\infty \frac1{8i^2} > \sum_{i=n+1}^\infty \frac18 \left(\frac1i-\frac1{i+1}\right) = \frac1{8(n+1)}.$

(4)

A továbbiakban az (n+1)x_n sorozat viselkedését fogjuk pontosabban vizsgálni. Két esetet fogunk megkülönböztetni.

1. eset: az (n+1)x_n sorozatnak van (véges) torlódási pontja. Mivel véges sok kivétellel $(n+1)x_n>\frac18$ , az összes torlódási pont az $[\frac18,\infty)$ félegyenesen van. Jól ismert, hogy a torlódási pontok között van legkisebb. (A legkisebb torlódási pontot hívják a sorozat limesz inferiorának.) Jelöljük c-vel a legkisebb torlódási pontot. Ekkor tehát $c\ge\frac18$ , és létezik egy olyan $n_1<n_2<\ldots$ indexsorozat, amire (n_k+1)x_{n_k} $\to$ c.

Mivel c-nél már nincs kisebb torlódási pont, A Bolzano-Weierstrass-tétel miatt tetszőleges $\delta$ >0 esetén (n+1)x_n>c- $\delta$ véges sok n kivételével. Ezt beírva (3)-ba, majd (4)-hez hasonlóan összegezve, n_k>n₀ és $\delta$ $\le$ c esetén

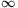$(n_k+1) x_{n_k} = (n_k+1) \sum_{i=n_k+1}^\infty (x_{i-1}-x_i) > (n_k+1) \sum_{i=n_k+1}^\infty \left(\frac{\frac14+\varepsilon}{2i^2} + 2x_{i-1}x_i \right) >$

$> (n_k+1) \sum_{i=n_k+1}^\infty \left(\frac{\frac14+\varepsilon}{2i(i+1)} + 2\frac{(c-\delta)^2}{i(i+1)}\right) =$

$= \left(\frac{\frac14+\varepsilon}2+2(c-\delta)^2\right) (n_k+1) \sum_{i=n_k+1}^\infty \left(\frac1i-\frac1{i+1}\right) = \frac{\frac14+\varepsilon}2+2(c-\delta)^2.$

A k $\to$ $\infty$ határátmenetből

$c = \lim (n_k+1) x_{n_k} \ge \frac{\frac14+\varepsilon}2+2(c-\delta)^2.$

Ezután a $\delta$ $\to$ +0 határátmenetet alkalmazva,

$c \ge \frac{\frac14+\varepsilon}2+2c^2$

$\left(2c-\frac12\right)^2 + \varepsilon \le 0,$

ami ellentmondás, mert a baloldal biztosan pozitív.

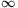2. eset: Az (n+1)x_n sorozatnak nincs (véges) torlódási pontja. A Bolzano-Weierstrass-tétel és a sorozat alulról korlátossága miatt ez azt jelenti, hogy bármely K valós számra (n+1)x_n>K véges sok kivétellel, azaz (n+1)x_n $\to$ $\infty$ .

Mivel (n+1)x_n 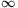$\to$ $\infty$ , van olyan n>n₀ index, amire 1<nx_n-1<(n+1)x_n. Ekkor azonban (3)-at alkalmazva,

$0< x_{n-1}-x_n - 2x_{n-1}x_n = \frac1{n+1}\Big(nx_{n-1}-(n+1)x_n\Big) + \frac{x_{n-1}}{n+1}\Big(1-2(n+1)x_n\Big),$

ami szintén ellentmondás, mert nx_n-1-(n+1)x_n és 1-2(n+1)x_n is negatív.

Ezzel minden esetben ellentmondásra jutottunk, és ezzel igazoltuk az állítást.

Megjegyzés. A feladat állításában az $\varepsilon$ tag lényeges, elhagyásával az állítás nem maradna igaz. Például az $a_n=\frac{n}{2n+1}$ sorozatra

$n^2 \big(4a_n(1-a_{n-1})-1 \big) = n^2 \left(\frac{4n}{2n+1}\bigg(1-\frac{n-1}{2n-1}\bigg)-1\right) = \frac{n^2}{4n^2-1} > \frac14.$

Statisztika:

6 dolgozat érkezett.

5 pontot kapott: Ágoston Tamás, Mester Márton, Omer Cerrahoglu, Strenner Péter.

1 pontot kapott: 2 versenyző.

A KöMaL 2012. januári matematika feladatai

6 dolgozat érkezett.
5 pontot kapott:	Ágoston Tamás, Mester Márton, Omer Cerrahoglu, Strenner Péter.
1 pontot kapott:	2 versenyző.

Már regisztráltál?
Új vendég vagy?