Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

Az A. 586. feladat (2013. március)

A. 586. Két konvex négyszög oldalai a1, a2, a3, a4, illetve A1, A2, A3, A4; területük t, illetve T. Igazoljuk, hogy

16tT \le \sum_{i=1}^4 a_i^2 \big(A_{i+1}^2+A_{i+2}^2+A_{i+3}^2-A_i^2\big) + 4a_1A_2a_3A_4 + 4A_1a_2A_3a_4.

(Az indexeket modulo 4 értjük.)

(5 pont)

A beküldési határidő 2013. április 10-én LEJÁRT.

Megoldásvázlat.

Lemma.

16t^2 \le \prod_{i=1}^4 (a_{i+1}+a_{i+2}+a_{i+3}-a_i),

és egyenlőség akkor áll, ha a négyszög húrnégyszög.

Bizonyítás. A területet úgy írjuk fel, hogy a négyszöget két háromszögre bontjuk. Jelölje \varphi az a1 és a2, 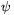\psi pedig az a3 és a4 oldalak közötti szöget; ekkor tehát

t = \frac12 a_1a_2\sin\varphi + \frac12 a_3a_4\sin\psi.

A két háromszögre felírva a koszinusztételt

a12+a22-2a1a2cos \varphi=a32+a42-2a3a4cos \psi;

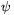átrendezve

a12+a22-a32-a42=2(a1a2cos \varphi-a3a4cos \psi).

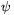Ezután

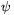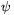16t2+(a12+a22-a32-a42)2=4(a1a2sin \varphi+a3a4sin \psi)2+4(a1a2cos \varphi-a3a4cos \psi)2=            

            =4a12a22+4a32a42-8a1a2a3a4cos (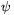\varphi+\psi)\le4a12a22+4a32a42+8a1a2a3a4=4(a1a2+a3a4)2.

Akkor van egyenlőtlenség, ha cos (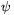\varphi+\psi)=-1, azaz 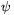\varphi+\psi=180o.

A becslést átrendezve,

16t2\le4(a1a2+a3a4)2-(a12+a22-a32-a42)2=(2(a1a2+a3a4)+(a12+a22-a32-a42))(2(a1a2+a3a4)-(a12+a22-a32-a42))=(*)

=((a1+a2)2-(a3-a4)2))((a3+a4)2-(a1-a2)2))=(a1+a2+a3-a4)(a1+a2-a3+a4)(a3+a4+a1-a2)(a3+a4-a1+a2).

(Bővebben lásd itt.)

A feladat megoldásához írjuk fel a Lemmát mindkét négyszögre a következő alakban (ez valójában a (*) sor, csak az a2 és az a3 változok szerepét felcseréltük):

16t2+(a12+a32-a22-a42)2\le4(a1a3+a2a4)2

16T2+(A12+A32-A22-A42)2\le4(A1A3+A2A4)2

A Cauchy-Schwarz-Bunyakovszkij egyenlőtlenségből

16tT+(a12+a32-a22-a42)(A12+A32-A22-A42)\le

\le \sqrt{16t^2 + (a_1^2+a_3^2-a_2^2-a_4^2)^2} \sqrt{16T^2 + (A_1^2+A_3^2-A_2^2-A_4^2)^2} \le 4(a_1a_3+a_2a_4)(A_1A_3+A_2A_4) =

=4a1A2a3A4+4A1a2A3a4+4a1a3A1A3+4a2a4A2A4\le4a1A2a3A4+4A1a2A3a4+2(a12A32+a32A12)+2(a22A42+a42A22).

Ezért

16tT\le4a1A2a3A4+4A1a2A3a4+2(a12A32+a32A12+a22A42+a42A22)-(a12+a32-a22-a42)(A12+A32-A22-A42)=

= \sum_{i=1}^4 a_i^2 \big(A_{i+1}^2+A_{i+2}^2+A_{i+3}^2-A_i^2\big) + 4a_1A_2a_3A_4 + 4A_1a_2A_3a_4.

A becslésekből leolvasható, hogy egyenlőség akkor van, ha két hasonló húrnégyszögről van szó.

Statisztika:

3 dolgozat érkezett.
5 pontot kapott:Janzer Olivér, Szabó 789 Barnabás.
1 pontot kapott:1 versenyző.

A KöMaL 2013. márciusi matematika feladatai