Az A. 590. feladat (2013. május)

A. 590. Határozzuk meg azokat az a egész számokat, amelyekhez létezik olyan egész együtthatós p(x) polinom, amelyre

$p\big(\big(\root3\of {a}\,\big)^2 + \root3\of {a}\,\big) = \big(\root3\of {a}\,\big)^2 - \root3\of {a}.$

A Vojtech Jarník verseny feladata alapján

(5 pont)

A beküldési határidő 2013. június 10-én LEJÁRT.

Megoldás. Ha a teljes köb, akkor a $p(x)=\root3\of {a^2}-\root3\of {a}$ (konstans) polinom megfelelő. A továbbiakban feltételezzük, hogy a nem teljes köb; ilyenkor $\root3\of{a}$ és $\root3\of{a^2}$ irracionális.

Szükségünk lesz a következő, jól ismert tényre.

Lemma. 1. Ha az u,v,w egész számokra $u+v\root3\of{a}+w\root3\of{a^2}=0$ , akkor u=v=w=0.

2. Minden valós szám legfeljebb egyféleképpen írható fel $u+v\root3\of{a}+w\root3\of{a^2}$ alakban.

Bizonyítás. 1. Tegyük fel, hogy mégis vannak olyan u,v,w egészek, amelyekre $u+ v\root3\of{a}+w\root3\of{a^2}=0$ , de u,v,w között 0-tól különböző is van. Mivel $\root3\of{a}$ és $\root3\of{a^2}$ irracionális, ez csak úgy lehetséges, ha u,v,w egyike sem 0.

Az x³+y³+z³-3xyz=(x+y+z)(x²+y²+z²-xy-xz-yz) azonosságot az x=u, $y=v\root3\of{a}$ , $z=w\root3\of{a^2}$ választással felírva láthatjuk, hogy

u³+av³+a²w³-3auvw=0.

(*)

Legyen q az a egyik olyan prímosztója, amelynek kitevője nem osztható 3-mal. (Mivel a nem teljes köb, van neki.) Tetszőleges n $\ne$ 0 egészre jelölje 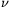$\nu$ _q(n) a q kitevőjét az n prímtényezős felbontásában.

Vegyük észre, hogy (*) baloldalán 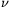$\nu$ _q(u³), 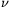$\nu$ _q(av³) és 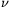$\nu$ _q(a²w³) különböző, mert mert már modulo 3 is különböznek. Továbbá

$\nu_q(3auvw) \ge \nu_q(auvw) = \frac13\nu_q(a^3u^3v^3w^3) = \frac{\nu_q(u^3)+\nu_q(av^3)+\nu_q(a^2w^3)}3 > \min\big(\nu_q(u^3),\nu_q(av^3),\nu_q(a^2w^3)\big).$

Ebből következik, hogy a 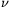$\nu$ _q(u³), 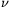$\nu$ _q(av³), 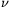$\nu$ _q(a²w³) és 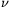$\nu$ _q(3auvw) kitevők között egyetlen legkisebb van; ekkor viszont a (*) baloldala nem lehet nulla.

2. Ha valamely u₁,u₂,v₁,v₂,w₁,w₂ egész számokra $u_1+v_1\root3\of{a}+w_1\root3\of{a^2}= u_2+v_2\root3\of{a}+w_2\root3\of{a^2}$ , akkor $(u_1-u_2)+(v_1-v_2)\root3\of{a}+(w_1-w_2)\root3\of{a^2}=0$ , így a lemma 1. része miatt u₁=u₂, v₁=v₂ és w₁=w₂.

Ezzel a lemmát bebizonyítottuk.

A feladat megoldásához a következőt bizonyítjuk:

Állítás. Tetszőleges p(x) egész együtthatós polinomra

$p\Big(\root3\of{a^2}+\root3\of{a}\Big) = u + v\root3\of{a} + w\root3\of{a^2}$

(**)

alkalmas egész u,v,w számpokkal, és $v\equiv w\pmod{a-1}$ .

Az állításunkat az p fokszáma szerinti indukcióval igazoljuk. Ha p(x) konstans polinom, akkor u=p(0) és v=w=0, és az állítás triviális. Tegyük fel tehát, hogy p foka legalább 1, és az állítást már igazoltuk alacsonyabb fokú polinomokra.

Írjuk p(x) a koövetkező alakban: p(x)=x^.P(x)+c, ahol P egész együtthatós polinom és c=p(0) egész szám. A P foka kisebb, mint a p foka, ezért az indukciós feltevés szerint

$P\Big(\root3\of{a^2}+\root3\of{a}\Big) = U + V\root3\of{a} + W\root3\of{a^2}$

alkalmas U,V,W egészekkel, amikre $V\equiv W\pmod{a-1}$ . Ezért

$p\Big(\root3\of{a^2}+\root3\of{a}\Big) = \Big(\root3\of{a^2}+\root3\of{a}\Big) \cdot P\Big(\root3\of{a^2}+\root3\of{a}\Big) + c =$

$= \Big(\root3\of{a^2}+\root3\of{a}\Big) \cdot \Big(U + V\root3\of{a} + W\root3\of{a^2}\Big) +c = (aV+aW+c) + (U+aW)\root3\of{a} + (U+V)\root3\of{a^2}$

ahonnan a p=aV+aW+c, v=U+aW, w=U+V választással (**) valóban teljesül. Végül, $a\equiv1\pmod{a-1}$ és $V\equiv W\pmod{a-1}$ miatt

$v = U+aW \equiv U+1\cdot V = w \pmod{a-1}.$

A Lemma és az Állítás miatt

$p\Big(\root3\of{a^2} + \root3\of {a}\,\Big) = 0 +(-1)\cdot \root3\of {a} +1\cdot \big(\root3\of {a}\,\big)^2$

csak akkor teljesülhet, ha $1\equiv-1\pmod{a-1}$ , azaz a-1 osztója 2-nek. Ez az a=2 és a=3 esetekban igaz. (Az a=0 és a=-1 esetekben a köbszám.) Ezekre az értékekre mutatunk egy-egy megfelelő polinomot.

Az a=2 esetben p(x)=-2x²+3x+8 megfelelő, mert

$p\Big(\root3\of2+\root3\of4\Big) = -2\Big(\root3\of2+\root3\of4\Big)^2 +3\Big(\root3\of2+\root3\of4\Big) +8 = \root3\of4-\root3\of2.$

Az a=3 esetben p(x)=-x²+2x+6 egy jó választás, mert

$p\Big(\root3\of3+\root3\of9\Big) = -\Big(\root3\of3+\root3\of9\Big)^2 +2\Big(\root3\of3+\root3\of9\Big) +6 = \root3\of9-\root3\of3.$

A feladatban előírt p polinom tehát akkor létezik, ha a köbszám, a=2, vagy pedig a=3.

Statisztika:

11 dolgozat érkezett.

5 pontot kapott: Herczeg József, Janzer Olivér, Maga Balázs, Szabó 789 Barnabás, Szabó 928 Attila, Williams Kada.

4 pontot kapott: Juhász 995 Mátyás Péter, Kúsz Ágnes, Sárosdi Zsombor, Török 928 Mihály.

0 pontot kapott: 1 versenyző.

A KöMaL 2013. májusi matematika feladatai

11 dolgozat érkezett.
5 pontot kapott:	Herczeg József, Janzer Olivér, Maga Balázs, Szabó 789 Barnabás, Szabó 928 Attila, Williams Kada.
4 pontot kapott:	Juhász 995 Mátyás Péter, Kúsz Ágnes, Sárosdi Zsombor, Török 928 Mihály.
0 pontot kapott:	1 versenyző.

Már regisztráltál?
Új vendég vagy?