Az A. 603. feladat (2013. december)

A. 603. Legyen $\alpha$ valós szám. Minden q pozitív egészre legyen $N_q(\alpha) = \min \left\{{\left|\alpha-\frac pq\right|} \colon {p \in \mathbb{Z}}\right\}$ , vagyis a legközelebbi olyan törttől való távolság, amely felírható q nevezővel (nem feltétlenül redukált alakban). Mutassuk meg, hogy az

$a_k= \frac{1}{\log k} \sum_{q=1}^{k} N_q(\alpha)$

sorozat konvergens.

(5 pont)

A beküldési határidő 2014. január 10-én LEJÁRT.

Megoldás. A megoldás folyamán $\| x\|$ -szel fogjuk jelölni az x távolságát a legközelebbi egész számtól. Ekkor tehát $0\le\| x\| \le\frac12$ . Könnyen ellenőrizhető, hogy tetszőleges x,y számokra és q pozitív egészre teljesülnek a következők:

$\big\| |x|\big\| =\| x\| ; \qquad \| x\| +\| y\| \ge \| x+y\| \ge \big|\| x\| -\| y\| \big|; \qquad N_q(x) = \frac{\| qx\| }{q}.$

A megoldásban többször meg fog jelenni a

$H_k = 1+\frac12+\frac13+\ldots+\frac1k$

összeg, a k-adik harmonikus szám. Erről jól ismert, hogy H_k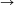 $\to$ $\infty$ ; kicsit pontosabban

log k<H_k $\le$ log k+1.

Legyen k $\ge$ 0 esetén $s_k=\sum_{i=1}^k \| i\alpha\|$ . A következőket fogjuk bizonyítani.

1. állítás. Az $\frac{s_k}k$ sorozat konvergens.

2. állítás. $\lim\left(\frac1{H_k}\sum_{i=1}^{k} N_i(\alpha)\right) = \lim\frac{s_k}k$ .

Az 1. álllítás bizonyítása abban az esetben, ha $\alpha$ racionális szám.

Legyen $\alpha=\frac{p}{q}$ , ahol p és q $\ge$ 1 relatív prím egész számok. Az $\| i\alpha\|$ sorozat q szerint periodikus; legyen $c=\frac1q\sum_{i=1}^q\| i\alpha\|$ egy periódus átlaga. A c szám 0 és $\frac12$ közé eső számok átlaga, így biztosan $0\le c\le\frac12$ .

Most tetszőleges k pozitív egészre összehasonlítjuk s_k-t kc-vel. Írjuk k-t k=k₁q+k₀ alakban, ahol k₁=[k/q], és a 0 $\le$ k₀<q szám a k osztási maradéka modulo q. Az $\sum_{i=1}^k\| i\alpha\|$ összeg k₁ teljes periódusból és k₀ további tagból áll, ezért

$s_k = \sum_{i=1}^k\| i\alpha\| = k_1\cdot qc + \sum_{i=1}^{k_0}\| i\alpha\|,$

$|s_k - kc| = \left|k_1\cdot qc + \sum_{i=1}^{k_0}\| i\alpha\| -(k_1q+k_0)c\right| = \left|\sum_{i=1}^{k_0}\| i\alpha\| - k_0c\right| \le \sum_{i=1}^{k_0}\left|\| i\alpha\| - c\right| \le k_0\cdot\frac12 < \frac{q}2.$

Ezt a becslést k-val osztva,

$\left|\frac{s_k}k-c\right| < \frac{q}{2k}.$

Ebből láthatjuk, hogy $\left|\frac{s_k}k-c\right|\to0$ , és így $\frac{s_k}k\to c$ .

Megjegyzés. Könnyű ellenőrizni, hogy

$c= \cases{ \frac14 & \text{ha {\it q} p\'aros,} \cr \frac14-\frac1{4q^2} & \text{ha {\it q} p\'aratlan.} \cr }$

(Lásd a (3) és (4) képleteket.)

Az 1. álllítás bizonyítása abban az esetben, ha $\alpha$ irracionális szám.

Azt bizonyítjuk be, hogy $\frac{s_k}k\to\frac14$ . Vegyünk egy tetszőleges 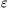$\varepsilon$ >0 valós számot; azt kell igazolnunk, hogy elég nagy k esetén $\left|\frac{s_k}k-\frac14\right|<\varepsilon$ .

Felhasználjuk Dirichlet approximációs tételét: létezik végtelen sok olyan $\frac{p}{q}$ racionális szám, amire

$\left|\alpha-\frac{p}{q}\right|<\frac1{q^2} .$

Válasszunk az ilyen törtek közül egy olyat, amire $q>\frac4{\varepsilon}$ .

Lemma. Tetszőleges x valós számra

$\left| \sum_{i=1}^q \| x+i\alpha \| - \frac{q}{4} \right| < 2.$

Bizonyítás. Legyen $\frac{r}{q}$ az x-hez legközelebbi, q nevezőjű tört; ekkor tehát $\left|x-\frac{r}{q}\right|\le\frac1{2q}$ .

A háromszög-egyenlőtlenség miatt

$\left| \sum_{i=1}^q \| x+i\alpha \| - \frac{q}{4} \right| \le \left| \sum_{i=1}^q \| x+i\alpha \| - \sum_{i=1}^q \left\| \frac{r}{q}+i\frac{p}{q} \right\| \right| + \left| \sum_{i=1}^q \left\| \frac{r}{q}+i\frac{p}{q} \right\| - \frac{q}{4} \right| \le$

$\le \sum_{i=1}^q \left| \| x+i\alpha \| -\left\| \frac{r}{q}+i\frac{p}{q} \right\| \right| + \left| \sum_{i=1}^q \left\| \frac{r+ip}{q} \right\| -\frac{q}{4} \right|.$

(1)

Az első összegben minden tag kicsi, ugyanis 0 $\le$ i $\le$ q esetén

$\left| \| x+i\alpha \| -\left\| \frac{r}{q}+i\frac{p}{q} \right\| \right| \le \left| x+i\alpha - \frac{r}{q}-i\frac{p}{q} \right| \le \left|x-\frac{r}{q}\right| + i\left|\alpha-\frac{p}{q}\right| \le \frac1{2q}+q\cdot \frac1{q^2} < \frac{3/2}q;$

így hát

$\sum_{i=1}^q \left| \| x+i\alpha \| -\left\| \frac{r}{q}+i\frac{p}{q} \right\| \right| \le q\cdot \frac{2/3}q = \frac32.$

(2)

A (1)-ben álló utolsó összeg becsléséhez vegyük figyelembe, hogy az r+p,r+2p,...,r+qp számok teljes maradékrendszert alkotnak modulo q. Ezért

$\sum_{i=1}^q \left\| \frac{r+ip}{q} \right\| = \sum_{i=1}^q \left\| \frac{i}{q} \right\|.$

Ha q páratlan, akkor

$\sum_{i=1}^q \left\| \frac{i}{q} \right\| = 2\left(\frac1q+\frac2q+\ldots+\frac{(q-1)/2}q\right) = \frac{q^2-1}{4q} = \frac{q}4 - \frac1{4q}.$

(3)

Ha pedig q páros, akkor

$\sum_{i=1}^q \left\| \frac{i}{q} \right\| = 2\left(\frac1q+\frac2q+\ldots+\frac{\frac{q}2-1}q\right) + \frac{\frac{q}2}{q} = \frac{q}4.$

(4)

Mindkét esetben igaz, hogy

$\left| \sum_{i=1}^q \left\| \frac{r+ip}{q} \right\| -\frac{q}{4} \right| \le \frac1{4q}.$

(5)

Ha (1)-be beírjuk (2)-t és (5)-t, azt kapjuk, hogy

$\left| \sum_{i=1}^q \| x+i\alpha \| - \frac{q}{4} \right| \le \frac32+\frac1{4q} < 2.$

Ezzel a lemmát igazoltuk.

Az 1. állítás bizonyításához legyen most k egész szám, amire $k>\frac{q}{2\varepsilon}$ . Írjuk a k számot k=k₁q+k₀ alakban, ahol k₁=[k/q], és 0 $\le$ k₀<q a k osztási maradéka modulo q. A lemmát az x=q $\alpha$ ,2q $\alpha$ ,...,k₁q $\alpha$ számokra alkalmazva,

$\left|\sum_{i=1}^q \| i\alpha\| - \frac{q}4 \right| < 2, \quad \left|\sum_{i=q+1}^{2q}q \| i\alpha\| - \frac{q}4 \right| < 2, \quad, \dots, \qquad \left|\sum_{i=(k_1-1)q+1}^{k_1q}q \| i\alpha\| - \frac{q}4 \right| < 2,$

továbbá triviálisan

$\left|\sum_{i=k_1q+1}^k \| i\alpha\| - \frac{k_0}4 \right| \le \sum_{i=k_1q+1}^k \left|\| i\alpha\|-\frac14\right| \le k_0\cdot\frac14.$

Ezeket mind összeadva,

$\left|s_k-\frac{k}4\right| \le k_1\cdot 2 + k_0\cdot\frac14 < \frac{2k}{q} + \frac{q}4.$

Osztva k-val,

$\left| \frac{s_k}k-\frac14\right| < \frac2q + \frac{q}{4k} <\frac\varepsilon2+\frac\varepsilon2 = \varepsilon.$

Tehát, ha $k>\frac{q}{2\varepsilon}$ , akkor $\left|\frac{s_k}k-\frac14\right|<\varepsilon$ . Ezzel igazoltuk, hogy $\frac{s_k}k\to\frac14$ .

A 2. álllítás bizonyítása.

Legyen $c=\lim \frac{s_k}k$ , és vegyünk ismét egy rögzített 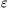$\varepsilon$ >0 számot. Azt akarjuk igazolni, hogy elég nagy k esetén $\left| \frac1{H_k}\sum_{i=1}^{k} N_i(\alpha) - c\right| < \varepsilon$ .

Mivel $\frac{s_k}{k}\to c$ , van egy olyan K pozitív egész szám, hogy k>K esetén $\left|\frac{s_k}k-c\right|<\frac{\varepsilon}2$ . Legyen $M=\max_{1\le i\le K}\left|\frac{s_k}k-c\right|$ . Ekkor tehát

$\left|\frac{s_k}k-c\right| \le \left\{\matrix{ M & {\rm ha~} i\le K, \cr \frac\varepsilon2 & {\rm ha~} i>K. \cr}\right.$

(6)

A bizonyítás kulcsa a következő, "Abel féle" átrendezés:

$\sum_{i=1}^{k} N_i(\alpha) = \sum_{i=1}^k \frac{\| i\alpha\|}{i} = \sum_{i=1}^k \frac{s_i-s_{i-1}}{i} = \sum_{i=1}^{k-1}\left(\frac1i-\frac1{i+1}\right)s_i + \frac{s_k}{k} = \sum_{i=1}^{k-1} \frac{\frac{s_i}{i}}{i+1} + \frac{s_k}{k}.$

(7)

Ha az összes előforduló $\| i\alpha\|$ szám helyére az "átlagos" c értéket, az N_q( $\alpha$ ) helyére $\frac{c}{q}$ -t, az s_i helyére pedig i^.c-t írunk, a (7) átrendezés így alakul:

$c H_k = \sum_{i=1}^k \frac{c}i = \sum_{i=1}^k \frac{ic-(i-1)c}{i} = \sum_{i=1}^{k-1}\left(\frac1i-\frac1{i+1}\right)ic + c = \sum_{i=1}^{k-1} \frac{c}{i+1} + c.$

(8)

(Ehhez persze nincs szükség az Abel-átrendezésre, a jobboldalon közvetlenül is felismerhetjük cH_k-t.)

Vegyük a (7) és a (8) különbségét, majd becsüljünk tagonként:

$\left|\sum_{i=1}^{k} N_i(\alpha) - cH_k \right| = \left| \sum_{i=1}^{k-1} \frac{\frac{s_i}{i} - c}{i+1} + \frac{s_k}{k}-c\right| \le \sum_{i=1}^{k-1} \frac{\left|\frac{s_i}{i}-c\right|}{i+1} + \left|\frac{s_k}{k}-c\right|.$

Most alkalmazzuk (6)-ot. Ha k>K, akkor

$\left|\sum_{i=1}^{k} N_i(\alpha) - cH_k \right| \le \sum_{i=1}^{K} \frac{\left|\frac{s_i}{i}-c\right|}{i+1} +\sum_{i=K+1}^{k-1} \frac{\left|\frac{s_i}{i}-c\right|}{i+1} + \left|\frac{s_k}{k}-c\right| <$

$< \sum_{i=1}^{K} \frac{M}{i+1} +\sum_{i=K+1}^{k-1} \frac{\frac\varepsilon2}{i+1} + \frac\varepsilon2 \le KM +\frac\varepsilon2 H_k.$

Most osszunk H_k-val:

$\left| \frac1{H_k}\sum_{i=1}^{k} N_i(\alpha) - c\right| < \frac{KM}{H_k} + \frac\varepsilon2.$

Ha k elég nagy (például $k>e^{2KM/\varepsilon}$ ), akkor $KM<\frac\varepsilon2 H_k$ , és így

$\left| \frac1{H_k}\sum_{i=1}^{k} N_i(\alpha) - c\right| < \varepsilon.$

Ezzel a 2. állítást is igazoltuk.

A feladat megoldása.

Mivel $\lim\frac{H_k}{\log k}=1$ , a 2. állításból azonnal következik, hogy

$\lim a_k = \lim\left( \frac{H_k}{\log k} \cdot \frac1{H_k}\sum_{i=1}^{k} N_i(\alpha) \right) = 1 \cdot c = c.$

Megjegyzés. A megoldás megadja az a_k sorozat határértékét is:

$\lim a_k = \cases{ \frac14-\frac1{4q^2} & \text{ha~} \alpha=\frac{p}{q} \text{\rm,~\'es~} q \text{\rm ~p\'aratlan;} \\ \frac14 & \text{egy\'ebk\'ent.} \\ }$

Statisztika:

1 dolgozat érkezett.

0 pontot kapott: 1 versenyző.

A KöMaL 2013. decemberi matematika feladatai

Már regisztráltál?
Új vendég vagy?