 |
Az A. 613. feladat (2014. március) |
A. 613. Adott az \(\displaystyle ABCD\) konvex négyszög \(\displaystyle AB\) oldalán az \(\displaystyle E\) és az \(\displaystyle F\), a \(\displaystyle BC\) oldalon a \(\displaystyle G\) és a \(\displaystyle H\), a \(\displaystyle CD\) oldalon az \(\displaystyle I\) és a \(\displaystyle J\), a \(\displaystyle DA\) oldalon pedig a \(\displaystyle K\) és az \(\displaystyle L\) pont úgy, hogy \(\displaystyle AE<AF<AB\), \(\displaystyle BG<BH<BC\), \(\displaystyle CI<CJ<CD\), és \(\displaystyle DK<DL<DA\). Az \(\displaystyle EJ\) szakasz \(\displaystyle GL\)-et és \(\displaystyle HK\)-t a \(\displaystyle P\), illetve az \(\displaystyle S\) pontban, az \(\displaystyle FI\) szakasz \(\displaystyle GL\)-et és \(\displaystyle HK\)-t a \(\displaystyle Q\), illetve az \(\displaystyle R\) pontban metszi. A \(\displaystyle P\) és az \(\displaystyle R\) pont az \(\displaystyle AC\), a \(\displaystyle Q\) és az \(\displaystyle S\) pont pedig a \(\displaystyle BD\) átlóra esik.
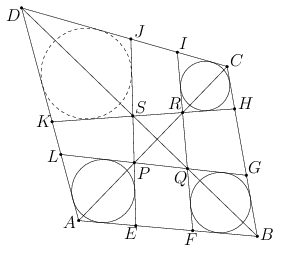
Mutassuk meg, hogy ha az \(\displaystyle AEPL\), \(\displaystyle BGQF\) és \(\displaystyle CIRH\) négyszögek érintőnégyszögek, akkor a \(\displaystyle DKSJ\) négyszög is érintőnégyszög.
A Zsautikov Olympia feladata alapján
(5 pont)
A beküldési határidő 2014. április 10-én LEJÁRT.
Statisztika:
1 dolgozat érkezett. 4 pontot kapott: Fehér Zsombor.
A KöMaL 2014. márciusi matematika feladatai
