 |
A B. 3817. feladat (2005. április) |
B. 3817. Az an sorozatot a következőképpen értelmezzük:
a1 2,
2, 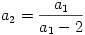 ,
, 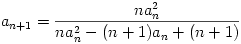 , ha n
, ha n 2.
2.
Bizonyítsuk be, hogy minden n-re teljesül az
a1+2a2+3a3+...+ nan=a1.a2.a3.....an
egyenlőség.
Javasolta: Kovács Béla, Szatmárnémeti
(5 pont)
A beküldési határidő 2005. május 17-én LEJÁRT.
Megoldás. Mivel az nx2-(n+1)x+(n+1) polinom diszkriminánsa, D=(n+1)2-4n(n+1)=(n+1)(1-3n)<0, n 2 esetén an+1 nevezőjében mindig pozitív szám áll, vagyis a sorozat minden tagja értelmezhető. Az is világos, hogy a2
2 esetén an+1 nevezőjében mindig pozitív szám áll, vagyis a sorozat minden tagja értelmezhető. Az is világos, hogy a2 1, ahonnan teljes indukcióval adódik, hogy an
1, ahonnan teljes indukcióval adódik, hogy an 1, ha n
1, ha n 2. A feladatban szereplő állítás bizonyítására térve világos hogy n=1 esetén az teljesül, ha pedig n=2, akkor könnyen ellenőrizhető:
2. A feladatban szereplő állítás bizonyítására térve világos hogy n=1 esetén az teljesül, ha pedig n=2, akkor könnyen ellenőrizhető:
A teljes indukciós bizonyításhoz tehát annyit kell csak igazolni, hogy n 2 esetén
2 esetén
Ezt általánosabban, n 1 esetén igazoljuk teljes indukcióval. Ha n=1, akkor
1 esetén igazoljuk teljes indukcióval. Ha n=1, akkor
Ha pedig n 2, és az
2, és az összefüggést már igazoltuk, akkor
Statisztika:
53 dolgozat érkezett. 5 pontot kapott: Dobos Gábor, Dudás László, Eisenberger András, Estélyi István, Fegyveres György, Gehér György, Gombkötő Tamás, Gyenizse Gergő, Hujter Bálint, Kisfaludi-Bak Sándor, Kiss-Tóth Christian, Komáromy Dani, Kónya 495 Gábor, Kutas Péter, Lorántfy Bettina, Lovász László Miklós, Mátyás Péter, Mészáros Gábor, Nagy 224 Csaba, Nagy 235 János, Nagy 317 Péter, Németh 007 Zsolt, Páldy Sándor, Sóvágó Sándor, Szabó 108 Tamás, Szalkai Balázs, Szalóki Dávid, Szegvári Gábor, Tossenberger Anna, Ureczky Bálint. 4 pontot kapott: Blázsik Zoltán, Bodzsár Erik, Bogár 560 Péter, Csaba Ákos, Csató László, Cseh Ágnes, Csorba János, Dányi Zsolt, Fegyverneki Dániel, Horváth 017 Zoltán, Kardos Kinga Gabriela, Kovács 111 Péter, Pálovics Róbert, Poronyi Balázs, Strenner Balázs, Szirmai Péter, Tomon István, Tóth 666 László Márton, Udvari Balázs. 3 pontot kapott: 3 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2005. áprilisi matematika feladatai
