Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány

Már regisztráltál?
Új vendég vagy?

A B. 3925. feladat (2006. szeptember)

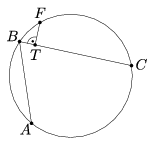
B. 3925. Az ABC körív F felezőpontjának az ABC töröttvonalon levő merőleges vetületét jelölje T. Bizonyítsuk be, hogy T felezi a töröttvonal hosszát.

(4 pont)

A beküldési határidő 2006. október 16-án LEJÁRT.

Megoldás: Jelölje a BAC szög nagyságát $\alpha$ , a BCA szögét $\gamma$ . Az ábrának megfelelően $\alpha$ > $\gamma$ . Az F ponton keresztül a BC húrral párhuzamos egyenes a körívet egy további F' pontban metszi, melynek vetülete a BC szakaszra legyen T'. A BC egyenesen a B,T,T',C pontok ebben a sorrendben követik egymást. Mivel BT=T'C és TT'=FF', elegendő az AB=FF' állítást igazolni. A kerületi szögek tétele értelmében ez egyenértékű azzal, hogy a C pontból az FF' húr is $\gamma$ szög alatt látszik.

Az AFC szög nagysága, akárcsak az ABC szögé, 180^o- $\alpha$ - $\gamma$ , ezért az FCA, az FAC és így az FBC és F'CB szög is egyaránt ( $\alpha$ + $\gamma$ )/2. Ezért az FCB szög ( $\alpha$ - $\gamma$ )/2, és így az F'CF szög valóban $\gamma$ .

Statisztika:

214 dolgozat érkezett.

4 pontot kapott: 148 versenyző.

3 pontot kapott: 34 versenyző.

2 pontot kapott: 13 versenyző.

1 pontot kapott: 10 versenyző.

0 pontot kapott: 9 versenyző.

A KöMaL 2006. szeptemberi matematika feladatai

214 dolgozat érkezett.
4 pontot kapott:	148 versenyző.
3 pontot kapott:	34 versenyző.
2 pontot kapott:	13 versenyző.
1 pontot kapott:	10 versenyző.
0 pontot kapott:	9 versenyző.