 |
A B. 3980. feladat (2007. február) |
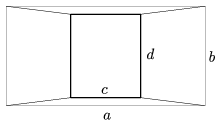
B. 3980. Az ábrán felülnézetben látható poliéder ,,alaplapjai'' párhuzamos téglalapok, oldalélei egyenlő hosszúak, magassága m. Valaki a poliéder térfogatára a következő képletet találta:
Igaz-e, hogy a képlet megadja a test térfogatát?
(3 pont)
A beküldési határidő 2007. március 19-én LEJÁRT.
Megoldás: Vágjuk fel a poliédert 9 részre a fedőlap éleire illeszkedő függöleges síkok segítségével. A középső rész egy téglatest lesz, melynek térfogata mcd. A téglatest oldallapjaihoz illeszkedő 4 rész közül két-két szemköztit összetolva egy-egy háromszög alapú hasábot kapunk, melyek térfogata , illetve
. Végül a négy sarokrészt összeillesztve egy téglalap alapú gúla keletkezik, melynek térfogata
. Ezt a négy térfogatmennyiséget összeadva kis átalakítás után valóban a talált képletet kapjuk.
Statisztika:
163 dolgozat érkezett. 3 pontot kapott: 97 versenyző. 2 pontot kapott: 20 versenyző. 1 pontot kapott: 32 versenyző. 0 pontot kapott: 14 versenyző.
A KöMaL 2007. februári matematika feladatai
