 |
A B. 4082. feladat (2008. április) |
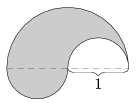
B. 4082. Az ábrán egy olyan síkidom látható, amellyel nem lehet egy egységsugarú félkört lefedni, de két egybevágó példányával már lefedhető egy egységsugarú kör. Létezik-e konvex síkidom is ugyanezzel a tulajdonsággal?
Kvant nyomán
(4 pont)
A beküldési határidő 2008. május 15-én LEJÁRT.
Megoldás: Jelöljük ki az egységsugarú körvonalon egy négyzet csúcsait, és annak két párhuzamos oldalával vágjunk le a körből egy-egy szeletet. A C egységkörből így megmaradó K síkidom konvex, hiszen előáll három konvex halmaz - a kör és két félsík - metszeteként. Ezen felül még szimmetrikus is a kör O középpontjára. A síkidomot O körül 90o-kal elforgatva, az eredeti és az elforgatott példány a kört lefedi. Csupán az eredeti példánnyal viszont nem lehet egy egységsugarú félkört lefedni. Ha ugyanis ez igaz lenne, akkor a lefedett F félkör átmérője a C körben is átmérő lenne, vagyis F-nek is O lenne a középpontja. Mivel K O-ra nézve szimmetrikus, K lefedné egyben F-nek O-ra vonatkozó tükörképét is, így az egész C kört is, ami viszont nem igaz. A K síkidom tehát rendelkezik a kívánt tulajdonsággal.
Statisztika:
86 dolgozat érkezett. 4 pontot kapott: Angyal Levente, Aujeszky Tamás, Backhausz Tibor, Bartha Zsolt, Blázsik Zoltán, Bodor Bertalan, Bunth Gergely, Cséke Balázs, Csere Kálmán, Dinh Hoangthanh Attila, Éles András, Fonyó Dávid, Frankl Nóra, Gőgös Balázs, Grósz Dániel, Huszár Kristóf, Kalina Kende, Kiss 243 Réka, Kiss 542 Robin, Kiss 716 Eszter, Konkoly 001 Csaba, Márkus Bence, Mészáros András, Mezei Márk, Muszka Balázs, Müller Márk, Nagy 648 Donát, Nguyen Milán, Palincza Richárd, Pap Máté, Perjési Gábor, Prok Tamás, Réti Dávid, Salát Zsófia, Somogyi Ákos, Szabó 895 Dávid, Szabó Tamás 492, Szőke Nóra, Tossenberger Anna, Tóth 222 Barnabás, Török Lajos, Tubak Dániel, Varga 171 László, Wang Daqian, Weisz Ágoston. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 8 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 25 versenyző.
A KöMaL 2008. áprilisi matematika feladatai
